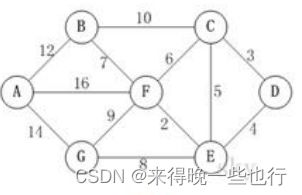
最小生成树（普里姆算法和克鲁斯卡尔算法）

1、基本介绍

 2、普里姆算法

 普里姆算法

---

---

---

package algorithm;

import java.util.Arrays;

public class PrimDemo {
    public static final int MAX_VALUE = 10000;
    public static void main(String[] args) {
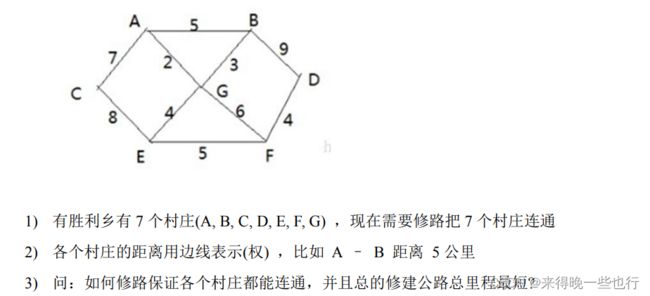
        char[] villages = new char[]{'A','B','C','D','E','F','G'};
        int[][] paths = {
                {MAX_VALUE, 5, 7, MAX_VALUE, MAX_VALUE, MAX_VALUE, 2},
                {5, MAX_VALUE, MAX_VALUE, 9, MAX_VALUE, MAX_VALUE, 3},
                {7, MAX_VALUE, MAX_VALUE, MAX_VALUE, 8, MAX_VALUE, MAX_VALUE},
                {MAX_VALUE, 9, MAX_VALUE, MAX_VALUE, MAX_VALUE, 4, MAX_VALUE},
                {MAX_VALUE, MAX_VALUE, 8, MAX_VALUE, MAX_VALUE, 5, 4},
                {MAX_VALUE, MAX_VALUE, MAX_VALUE, 4, 5, MAX_VALUE, 6},
                {2, 3, MAX_VALUE, MAX_VALUE, 4, 6, MAX_VALUE}
        };
        Graph graph = createCountrySide(villages, paths);
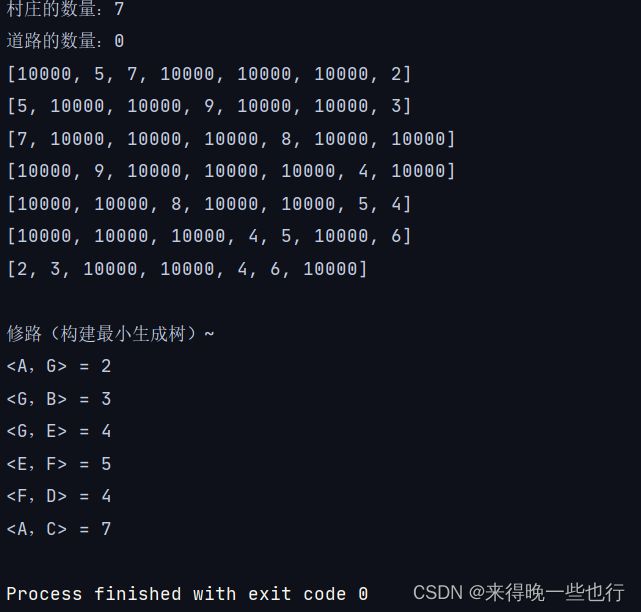
        System.out.println("村庄的数量：" + graph.vertexsNum);
        System.out.println("道路的数量：" + graph.edgesNum);
        graph.traverse();
        System.out.println("修路（构建最小生成树）~");
        prim(graph, 0);
    }

    //  构造最小生成树（修路）
    private static void prim(Graph graph, int startIndex) {
        int minWeight = MAX_VALUE;                      // 用于标记出权值最小的边
        int[] visited = new int[graph.vertexsNum];      // 用于标记顶点是否被访问
        visited[startIndex] = 1;                        // 标记当前顶点为已访问顶点
        int index1 = -1, index2 = -1;                   // 用于指向边权值最小的两个节点
        for (int k = 0; k < graph.vertexsNum - 1; k++) {// 如果有n个顶点，则有n-1条边
            for (int i = 0; i < visited.length; i++) {  // 对每个已访问顶点（子集）进行遍历，如：、、，找出与它们有关的最短边
                for (int j = 0; j < graph.vertexsNum; j++) {
                    if (visited[i] == 1 && visited[j] == 0 && graph.edges[i][j] < minWeight) { // 此处可优化
                        minWeight = graph.edges[i][j];
                        index1 = i;
                        index2 = j;
                    }
                }
            }
            //  一轮循环后，以该顶点为起点的最小边已经找出来了
            System.out.println("<" + graph.vertexs[index1] + "，"+ graph.vertexs[index2]+"> = " + minWeight);
            visited[index2] = 1; // 将当前边权值最小的顶点标记为已访问
            minWeight = MAX_VALUE; // 每次对下一轮中的顶点进行遍历前，都要重置minWeight
        }

    }

    //  将整个图构建起来（村庄）
    private static Graph createCountrySide(char[] villages, int[][] paths) {
        Graph graph = new Graph(villages.length);
        for (int i = 0; i < villages.length; i++) {
            graph.vertexs[i] = villages[i];             // 初始化图顶点
            for (int j = 0; j < paths.length; j++) {
                graph.edges[i][j] = paths[i][j];        // 初始化图的边
            }
        }
        return graph;
    }
}

class Graph{
    public int vertexsNum;
    public int edgesNum;
    public char[] vertexs;
    public int[][] edges;
    public Graph(int vertexsNum) {
        this.vertexsNum = vertexsNum;
        this.edgesNum = 0;
        this.vertexs = new char[vertexsNum];
        edges = new int[vertexsNum][vertexsNum];
    }

    public void traverse() {
        for (int[] edge : this.edges) {
            System.out.println(Arrays.toString(edge));
        }
        System.out.println();
    }
}

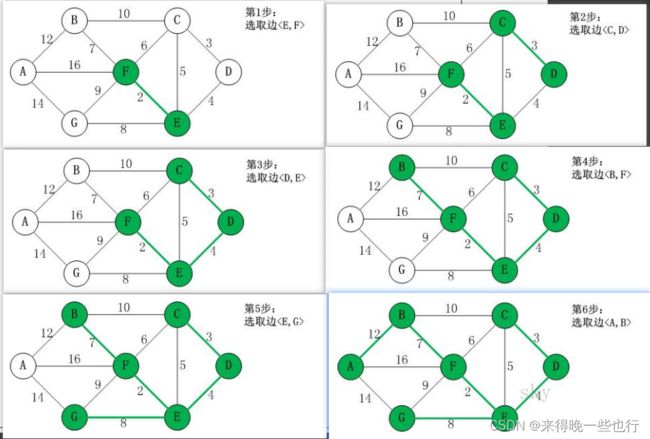
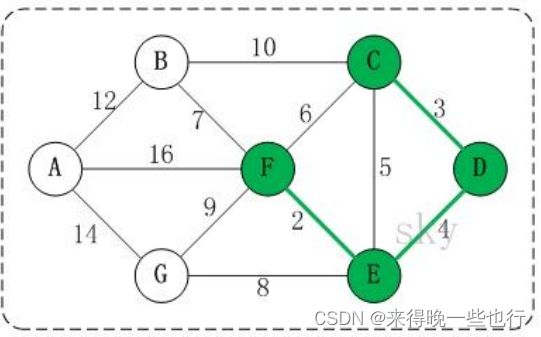
3、卡鲁斯卡尔算法

 克鲁斯卡尔算法

 重点：

---

---

---

package algorithm.kruskal;
import java.util.Arrays;
import java.util.Comparator;

public class KruskalDemo {
    private static final int INF = 10000;
    public static void main(String[] args) throws NullPointerException{
        char[] station = {'A','B','C','D','E','F','G'};
        int[][] distance = {
                {0, 12, INF, INF, INF, 16, 14},
                {12, 0, 10, INF, INF, 7, INF},
                {INF, 10, 0, 3, 5, 6, INF},
                {INF, INF,3 , 0, 4, INF, INF},
                {INF, INF, 5, 4, 0, 2, 8},
                {16, 7, 6, INF, 2, 0, 9},
                {14, INF, INF, INF, 8, 9, 0},
        };
        Graph graph = createCity(station, distance);
        graph.traverse();

        Edge[] seqEdges = getEdges(graph);     // 获取所有有效边
        System.out.println("各个站点的距离：");
        print(seqEdges);

        Edge[] res = kruskal(graph, seqEdges); // 获取权值最小且不成环的边
        System.out.println("总的修建公路总里程最短（最小生成树）：");
        print(res);

    }

    private static Edge[] kruskal(Graph graph, Edge[] seqEdges) {
        int[] ends = new int[graph.vertexsNum];      // 存放顶点对应终点（终点的下标）
        Edge[] res = new Edge[graph.vertexsNum];     // 存放最短距离（结果数组）——（n个顶点，n-1条边）
        int index = 0;                               // 结果数组的下标索引
        for (int i = 0; i < seqEdges.length; i++) {  // 遍历所有存在的边
          if (seqEdges[i] == null)                   // 碰到null时，所有存在的边已遍历完，退出循环
              break;
            char start = seqEdges[i].start;           // 获取该边的起点
            char end = seqEdges[i].end;               // 获取该边的终点
            int startIndex = graph.getIndex(start);   // 获取起点的下标
            int endIndex = graph.getIndex(end);       // 获取终点的下标
            int endPoint1 = getEnd(ends, startIndex); // 获取起点对应的终点（ends[]）
            int endPoint2 = getEnd(ends, endIndex);   // 获取终点对应的终点（ends[]）
            if (endPoint1 != endPoint2) {             // 两个点的终点不一样，说明不构成环
                ends[endPoint1] = endPoint2;          // 标注该顶点对应的终点
                res[index++] = seqEdges[i];           // 将该边添加到结果数组
            }
        }
        return res;
    }

    //  打印数组
    private static void print(Edge[] temp) {
        for (int i = 0; i < temp.length - 1; i++) {
            if (temp[i] != null)
                System.out.println(temp[i]);
        }
        System.out.println();
    }

    //  根据传入的顶点下标，获取该顶点所在边对应的终点。其中下标为起点，下标对应的值为终点
    //  如果该顶点与其它顶点不存在边，则终点就是它自身
    private static int getEnd(int[] ends, int index) {
        while(ends[index] != 0) {
            index = ends[index];
        }
        return index;
    }

    //  得到有效边的数组（按从小到大顺序）
    private static Edge[] getEdges(Graph graph) {
        int index = 0;
        Edge[] seqEdges = new Edge[graph.vertexsNum*graph.vertexsNum];
        for (int i = 0; i < graph.vertexsNum; i++) {
            for (int j = i + 1; j < graph.vertexsNum; j++) {
                if (graph.edges[i][j] != INF) {
                    char start = graph.vertexs[i];
                    char end = graph.vertexs[j];
                    int weight = graph.edges[i][j];
                    seqEdges[index++] = new Edge(start, end, weight);
                }
            }
        }

        //  按从小到大排序
         /*
                首先使用Comparator的nullsLast方法来比较weight，这个方法会把元素看作null值的元素看作最大，
                从而避免空指针异常；然后再使用thenComparing方法来比较其他成员变量，
                这个方法会在weight相等时，继续按照compareTo方法进行比较。这样处理后，就可以在保留原有排序规则的基础上，
                正确地对数组进行排序，即把空值放在数组的最后面。
         */
        Arrays.sort(seqEdges, Comparator.nullsLast(
                Comparator.comparing(Edge::getWeight)
                        .thenComparing(Edge::compareTo)
                )
        );

        return seqEdges;
    }

    private static Graph createCity(char[] station, int[][] distance) {
        Graph graph = new Graph(station.length);
        for (int i = 0; i < station.length; i++) {
            graph.vertexs[i] = station[i];
            for (int j = 0; j < distance.length; j++) {
                graph.edges[i][j] = distance[i][j];
            }
        }
        return graph;
    }
}

class Graph{
    public int vertexsNum;
    public int edgesNum;
    public char[] vertexs;
    public int[][] edges;
    public Graph(int vertexsNum) {
        this.vertexsNum = vertexsNum;
        this.edgesNum = 0;
        this.vertexs = new char[vertexsNum];
        edges = new int[vertexsNum][vertexsNum];
    }

    public void traverse() {
        System.out.println("公交站点分布如下：");
        for (int[] edge : this.edges) {
            System.out.println(Arrays.toString(edge));
        }
        System.out.println();
    }

    //  获取字符对应的下标
    public int getIndex(char ch) {
        for (int i = 0; i < vertexsNum; i++) {
            if (this.vertexs[i] == ch) {
                return i;
            }
        }
        return -1;
    }
}

//  用来存储有效边
class Edge implements Comparable{
    public char start;  // 起点
    public char end;    // 终点
    public int weight; // 权值（距离）
    public Edge(char start, char end, int weight) {
        this.start = start;
        this.end = end;
        this.weight = weight;
    }

    public int getWeight() {
        return this.weight;
    }

    @Override
    public int compareTo(Edge o) {
        return this.weight - o.weight;
    }

    @Override
    public String toString() {
        return "<"+ this.start + "，"+ this.end + "> = " + this.weight;
    }
}