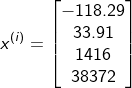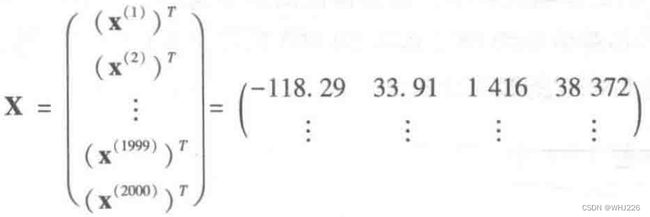机器学习实战(2)——端到端的机器学习项目
目录
1 框架问题
2 选择性能指标
2.1 均方根误差(RMSE)
2.2 平均绝对误差(MAE)
3 获取数据
4 创建测试集
5 从数据探索和可视化中获得洞见
5.1 将地理数据可视化
5.2 寻找相关性
5.3 试验不同属性的组合
6 机器学习算法的数据准备
6.1 数据清理
6.2 处理文本和分类属性
6.3 特征缩放
6.4 转换流水线
本篇中,我们将学习一个端到端的项目案例,假设我们是一个房地产公司新雇佣的数据科学家,以下是我们将会经历的主要步骤:
- 观察大局
- 获得数据
- 从数据探索和可视化中获得洞见
- 机器学习算法的数据准备
- 选择和训练模型
- 微调模型
- 展示解决方案
- 启动、监控和维护系统
1 框架问题
你问老板的第一个问题,应该是询问业务目标是什么,因为建立模型本身可能不是最终的目标。公司期望知道如何使用这个模型,如何从中获益?这才是重要的问题,因为这将决定你怎么设定问题,选择什么算法,使用什么测量方式来评估模型的性能,以及应该花多少精力来进行调整。
老板回答说,这个模型的输出(对一个区域房价中位数的预测)将会跟其他许多信号一起被传输给另一个机器学习系统(如下图)。而这个下游系统将被用来决策一个给定的区域是否值得投资。因为直接影响到收益,所以正确获得这个信息至关重要。
要向老板询问的第二个问题,是当前的解决方案(如果有的话)。你可以将其当作参考, 也能从中获得解决问题的洞察。老板回答说,现在是由专家团队在手动估算区域的住房价格——一个团队持续收集最新的区域信息(不包括房价中位数),然后使用复杂的规则来进行估算。既昂贵又耗时,而且估算结果还不令人满意,显著误差率高达15%。
好的,有了这些信息,我们现在可以开始设计系统了。显然,这是一个典型的监督式学习任务,因为已经给出了标记的训练示例(每个实例都有预期的产出,也就是该地区的房价中位数)。并且这也是一个典型的回归任务,因为你要对某个值进行预测。更具体地说,这是一个多变量回归问题,因为系统要使用多个特征进行预测(使用到区域的人口、收入中位数等)。
2 选择性能指标
2.1 均方根误差(RMSE)
回归问题的典型性能指标是均方根误差(RMSE),它测量的是预测过程中,预测错误的标准偏差。例如,RMSE等于50000 就意味着,系统的预测值中约68%落在50000美元之内,约95%落在100000美元之内。(一种常见的特征分布是呈钟形态的分布,称为正态分布(也叫高斯分布), “68-95-99.7”的规则是指:大约68%的值落在1![]() 内,95%落在2
内,95%落在2![]() 内,99.7%落在3
内,99.7%落在3![]() 内。)
内。)
均方根误差(RMSE):
公式符号:
- m是在测量RMSE时,所使用的数据集中实例的数量。
- 例如,如果你在评估RMSE时使用的验证集里包含2000个区域,则m=2000。
是数据集中,第
个实例的所有特征值的向量(标签特征除外),
是标签 (也就是我们期待该实例的输出值)。
- 例如,如果数据集的第一个区域位于经度-118.29° ,纬度33.91°,居民数量为1 416,平均收入为38 372美元,房价中位数为156 400美元(暂且忽略其他特征),那么:
- X是数据集中所有实例的所有特征值的矩阵(标记特征除外)。每个实例为一行,也就是说,第
行等于
的转置矩阵,记作
。
- h是系统的预测函数,也称为一个假设。当给定系统一个实例的特征向量
,它会输出一个预测值
(
读作“y-hat”)。
- 例如,如果系统预测第一个区域的房价中位数为158 400美元,则
=158 400。该区域的预测误差为
= 2 000。
- RMSE(X,h)是使用假设h在示例上测量的成本函数。
2.2 平均绝对误差(MAE)
当有很多离群区域时,我们可以考虑使用平均绝对误差(或称平均绝对偏差)。
平均绝对误差(MAE):
均方根误差和平均绝对误差两种方法都是测量两个向量之间的距离:预测向量和目标值向量。距离或者范数的测度可能有多种:
3 获取数据
以下代码均在jupyter中运行。
通过head()方法显示数据前五行信息。
import pandas as pd
#1、获取数据
data=pd.read_csv("E:\PYTHON\housing.csv")
#2、head()方法显示数据前五行信息
data.head()运行结果如下:
longitude latitude housing_median_age total_rooms total_bedrooms population households median_income median_house_value ocean_proximity
0 -122.23 37.88 41.0 880.0 129.0 322.0 126.0 8.3252 452600.0 NEAR BAY
1 -122.22 37.86 21.0 7099.0 1106.0 2401.0 1138.0 8.3014 358500.0 NEAR BAY
2 -122.24 37.85 52.0 1467.0 190.0 496.0 177.0 7.2574 352100.0 NEAR BAY
3 -122.25 37.85 52.0 1274.0 235.0 558.0 219.0 5.6431 341300.0 NEAR BAY
4 -122.25 37.85 52.0 1627.0 280.0 565.0 259.0 3.8462 342200.0 NEAR BAY每一行代表一个区,总共有10个属性。
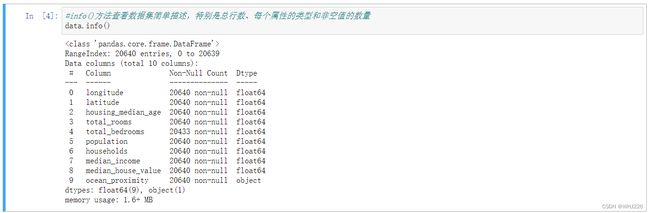
通过info()方法查看数据集简单描述,特别是总行数、每个属性的类型和非空值的数量。
#info()方法查看数据集简单描述,特别是总行数、每个属性的类型和非空值的数量
data.info()运行结果如下:
RangeIndex: 20640 entries, 0 to 20639
Data columns (total 10 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 longitude 20640 non-null float64
1 latitude 20640 non-null float64
2 housing_median_age 20640 non-null float64
3 total_rooms 20640 non-null float64
4 total_bedrooms 20433 non-null float64
5 population 20640 non-null float64
6 households 20640 non-null float64
7 median_income 20640 non-null float64
8 median_house_value 20640 non-null float64
9 ocean_proximity 20640 non-null object
dtypes: float64(9), object(1)
memory usage: 1.6+ MB 注意,total_bedrooms这个属性只有20 433个非空值,这意味着有207个区域确实这个特征,后面我们会学习到缺失值处理的方法。
所有属性的字段都是数字,除了ocean_proximity。它的类型是object,因此它可以是任何类型的Python对象,不过我们是从CSV文件中加载了该数据,所以它必然是文本属性。通过查看前五行,你可能会注意到,该列中的值是重复的,这意味着它有可能是一个分类属性。我们可以使用value_counts()方法查看有多少种分类存在,每种类别下分别有多少个区域:
#value_counts()方法查看多少种分类存在
data["ocean_proximity"].value_counts()运行结果如下:
<1H OCEAN 9136
INLAND 6551
NEAR OCEAN 2658
NEAR BAY 2290
ISLAND 5
Name: ocean_proximity, dtype: int64通过describe()方法查看数值属性的摘要:
#describe()方法查看数值属性
data.describe()运行结果如下:
longitude latitude housing_median_age total_rooms total_bedrooms population households median_income median_house_value
count 20640.000000 20640.000000 20640.000000 20640.000000 20433.000000 20640.000000 20640.000000 20640.000000 20640.000000
mean -119.569704 35.631861 28.639486 2635.763081 537.870553 1425.476744 499.539680 3.870671 206855.816909
std 2.003532 2.135952 12.585558 2181.615252 421.385070 1132.462122 382.329753 1.899822 115395.615874
min -124.350000 32.540000 1.000000 2.000000 1.000000 3.000000 1.000000 0.499900 14999.000000
25% -121.800000 33.930000 18.000000 1447.750000 296.000000 787.000000 280.000000 2.563400 119600.000000
50% -118.490000 34.260000 29.000000 2127.000000 435.000000 1166.000000 409.000000 3.534800 179700.000000
75% -118.010000 37.710000 37.000000 3148.000000 647.000000 1725.000000 605.000000 4.743250 264725.000000
max -114.310000 41.950000 52.000000 39320.000000 6445.000000 35682.000000 6082.000000 15.000100 500001.000000需要注意的是,这里的空值会被忽略(因此本例中, total_bedrooms的count是20 433而不是20 640)。std行显示的是标准差(用来测量数值的离散程度)。25%、50%和75%行显示相应的百分位数:百分位数表示一组观测值中给定百分比的观测值都低于该值。例如,对于housing_ median_age 的值, 25% 的区域低于18,50%的区域低于29,以及75%的区域低于 37。这些通常被称为:百分之二十五分位数(或者第一四分位数)、中位数以及百分之 七十五分位数(或者第三四分位数)。
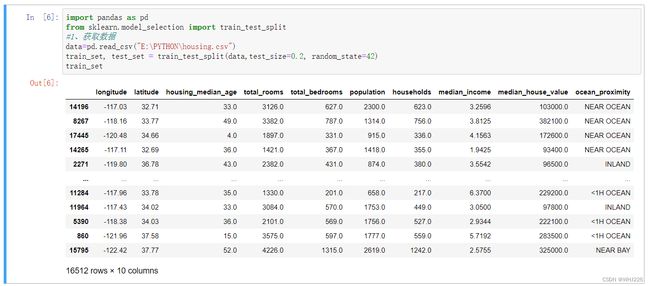
4 创建测试集
import pandas as pd
from sklearn.model_selection import train_test_split
#1、获取数据
data=pd.read_csv("E:\PYTHON\housing.csv")
train_set, test_set = train_test_split(data,test_size=0.2, random_state=42)要预测房价平均值,收入中位数是一个非常重要的属性,那么怎么确保在收入属性上,测试集能够代表整个数据集中各种不同类型的收入。
收入类别直方图
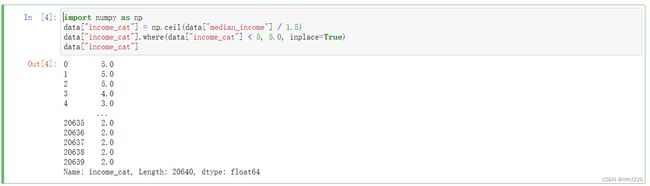
大多数收入中位数值聚集在2~5(万美元)左右,但也有一部分远远超过了6万。在数据集中,每一层都要有足够数量的实例,这一点至关重要,不然数据不足的层,其重要程度很有可能会被错估。也就是说,你不应该将层数分得太多,但每一层应该要足够大才行。下面这段代码是这样创建收入类别属性的:将收入中位数除以1.5 (限制收入类别的数量),然后使用ceil进行取整(得到离散类别),最后将所有大于5的类别合并为类别5:
import numpy as np
data["income_cat"] = np.ceil(data["median_income"] / 1.5)
data["income_cat"].where(data["income_cat"] < 5, 5.0, inplace=True)
data["income_cat"]运行结果如下:
0 5.0
1 5.0
2 5.0
3 4.0
4 3.0
...
20635 2.0
20636 2.0
20637 2.0
20638 2.0
20639 2.0
Name: income_cat, Length: 20640, dtype: float64现在,我们可以根据收入类别进行分层抽样。
from sklearn.model_selection import StratifiedShuffleSplit
split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state = 42)
for train_index, test_index in split.split(data, data["income_cat"]):
strat_train_set = data.loc[train_index]
strat_test_set = data.loc[test_index]我们可以看一下所有住房数据根据收入类别的比例分布:
data["income_cat"].value_counts()/len(data)运行结果如下:
3.0 0.350581
2.0 0.318847
4.0 0.176308
5.0 0.114438
1.0 0.039826
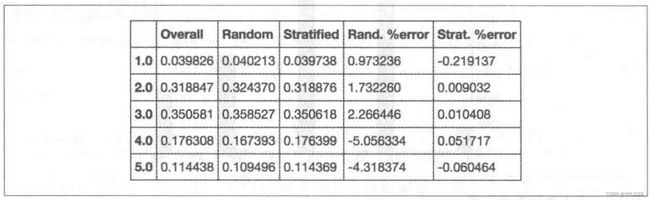
Name: income_cat, dtype: float64下图比较了三种不同数据集(完整数据集、分层抽样测试集、纯随机抽样的测试集)中收入类别的比例分布:
图中我们发现,分层抽样的测试集中的比例分布与完整数据集中的分布几乎一致,而纯随机抽样的测试结果则出现了重大偏离。
我们以上的操作,是在原有的数据列表基础上额外添加了income_cat属性,现在我们可以删除该属性并将数据恢复为原样:
for set in (strat_train_set, strat_test_set):
set.drop(["income_cat"], axis=1, inplace=True)小结:测试集的生成是机器学习项目中至关重要的一部分。
5 从数据探索和可视化中获得洞见
首先,把测试集放在一边,我们能探索的只有训练集。此外,如果训练集非常庞大,我们可以抽样一个探索集,这样后面的操作更简单快捷一些。不过我们这个案例的数据集非常小,完全可以直接在整个训练集上操作。让我们先创建一个副本,这样可以随便尝试而不损害训练集:
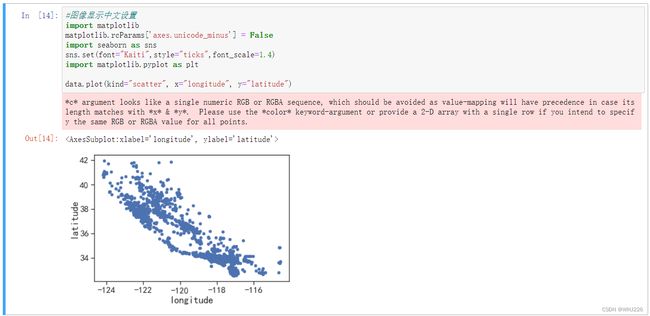
data = strat_test_set.copy()5.1 将地理数据可视化
未创建副本前数据地理分布图
创建副本后的数据地理分布图
#图像显示中文设置
import matplotlib
matplotlib.rcParams['axes.unicode_minus'] = False
import seaborn as sns
sns.set(font="Kaiti",style="ticks",font_scale=1.4)
import matplotlib.pyplot as plt
data.plot(kind="scatter", x="longitude", y="latitude")运行结果如下:
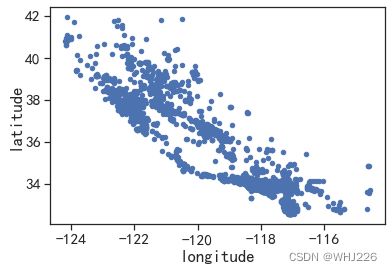
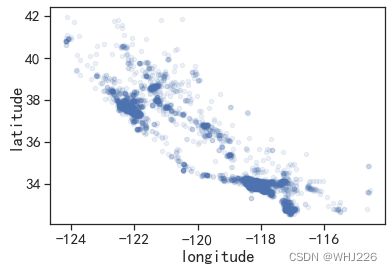
将alpha 选项设置为0.1,可以更清楚地看出高密度数据点的位置(见下图):
data.plot(kind="scatter", x="longitude", y="latitude", alpha=0.1)运行结果如下:
突出高密度区域的可视化
一般来说,我们的大脑非常善于从图片中发现模式,但是我们需要玩转可视化参数才能让这些模式凸显出来。现在,再来看看房价(见下图)。每个圆的半径大小代表了每个地区的人口数量(选项 s),颜色代表价格(选项c)。我们使用一个名叫jet的预定义颜色表(选项cmap)来进行可视化,颜色范围从蓝(低)到红(高):
data.plot(kind="scatter", x="longitude", y="latitude", alpha=0.4, s=data["population"]/100,
label="population",c="median_house_value",cmap=plt.get_cmap("jet"), colorbar=True,)
plt.legend()运行结果如下:
房屋价格
这张图片告诉我们房屋价格与地理位置(例如靠海)和人口密度息息相关,这点我们可能早已知晓。一个通常很有用方法是,使用聚类算法来检测主群体,然后再为各个聚类中心添加一个新的衡量邻近距离的特征。海洋邻近度可能就是一个很有用的属性。
5.2 寻找相关性
由于数据集不大,我们可以使用corr()方法轻松计算出每对属性之间的标准相关系数 (也称为皮尔逊相关系数):
corr_matrix = data.corr()现在看看每个属性与房屋中位数的相关性分别是多少:
corr_matrix["median_house_value"].sort_values(ascending=False)运行结果如下:
median_house_value 1.000000
median_income 0.691831
income_cat 0.650512
total_rooms 0.131435
housing_median_age 0.071357
households 0.071242
total_bedrooms 0.057568
population -0.016033
longitude -0.039987
latitude -0.150124
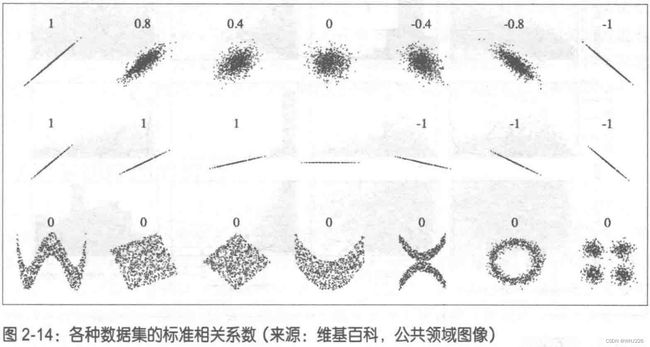
Name: median_house_value, dtype: float64相关系数的范围从-1变化到1。越接近1,表示有越强的正相关;比如,当收人中位数上升时,房价中位数也趋于上升。当系数接近于-1,则表示有强烈的负相关;注意看纬度和房价中位数之间呈现出轻微的负相关(也就是说,越往北走,房价倾向于下降)。最后,系数靠近0则说明二者之间没有线性相关性。图2-14显示了横轴和纵轴之间相关性系数的多种绘图。
相关系数仅测量线性相关性(“如果x上升,则y上升/下降”)。所以它有可能彻底遗漏非线性相关性(例如“如果x接近于零,则y会上升”)。注意上图最下面一排的图像,它们的相关性系数都是0,但是显然我们可以看出横轴和纵轴之间的关系并不是彼此完全独立的:这是非线性关系的例子。此外,图中第二行显示了相关性为1或-1时的例子,需要注意的是, 这个相关性跟斜率完全无关。这就好比是说,你本人用英寸来计量的身高与你用英尺甚至是纳米来计量的身高之间的相关系数等于1。
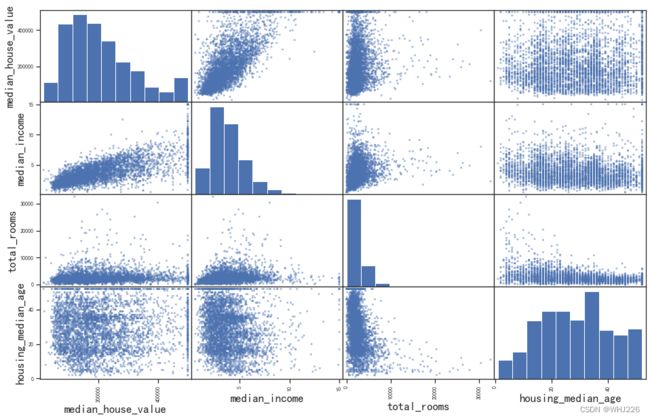
还有一种方法可以检测属性之间的相关性,就是使用Pandas的scatter matrix函数,它会绘制出每个数值属性相对于其他数值属性的相关性。这里我们仅关注那些与房价中位数属性最相关的,可算作是最有潜力的属性(见下图):
from pandas.plotting import scatter_matrix
attributes = ["median_house_value", "median_income", "total_rooms", "housing_median_age"]
scatter_matrix(data[attributes],figsize=(16,10))运行结果如下:
其中最有潜力能够预测房价中位数的属性是收入中位数,所以我们单独看看其相关性的散点图:
data.plot(kind="scatter", x="median_income", y="median_house_value", alpha=0.1)运行结果如下:
收入中位数和房价中位数
首先,二者相关性确实很强,我们可以清楚地看到上升的趋势,并且点也不是太分散。其次,前面我们提到过(未提及但存在)50万美元的价格上限在图中是一条清晰的水平线,不过除此以外,这张图还显示出几条不那么明显的直线:45万美元附近有一条水平线,35万美元附近也有一条,28万美元附近似乎隐约也有一条,再往下可能还有一些。为了避免我们的算法学习之后重现这些怪异数据,可能会尝试删除这些相应地区。
5.3 试验不同属性的组合
在准备给机器学习算法输人数据之前,我们要做的最后一件事应该是尝试各种属性的组合。比如,如果我们不知道一个地区有多少个家庭,那么知道一个地区的“房间总数”也没什么用。我们真正想要知道的是一个家庭的房间数量。同样地,单看“卧室总数”这个属性本身,也没什么意义,我们可能是想拿它和“房间总数”来对比,或者拿来同“每个家庭的人口数”这个属性结合也似乎挺有意思。我们来试着创建这些新属性:
data["rooms_per_household"] = data["total_rooms"]/data["households"]
data["bedrooms_per_room"] = data["total_bedrooms"]/data["total_rooms"]
data["population_per_household"] = data["population"]/data["households"]然后我们来看看关联矩阵:
corr_matrix = data.corr()
corr_matrix["median_house_value"].sort_values(ascending=False)运行结果如下:
median_house_value 1.000000
median_income 0.691831
income_cat 0.650512
rooms_per_household 0.192575
total_rooms 0.131435
housing_median_age 0.071357
households 0.071242
total_bedrooms 0.057568
population -0.016033
longitude -0.039987
population_per_household -0.135142
latitude -0.150124
bedrooms_per_room -0.240362
Name: median_house_value, dtype: float64这一轮的探索不一定要多么彻底:关键是迈开第一步,快速取得更深刻的理解,这将有助于我们获得非常棒的第一个原型。这也是个不断选代的过程:一旦我们的原型产生并且开始运行,我们可以分析它的输出以洞悉更多的见解,然后再次回到这个探索的步骤。
6 机器学习算法的数据准备
我们先回到一个干净的数据集(再次复制strat_train_set),然后将预测器和标签分开,因为这里我们不一定对它们使用相同的转换方式(需要注意drop()会创建一个数据副本,但是不影响strat_train_set):
data = strat_train_set.drop("median_house_value", axis=1)
data_labels = strat_train_set["median_house_value"].copy()6.1 数据清理
前面我们提到过total_bedrooms属性有部分缺失。所以我们要解决,有以下三种选择:
- 放弃这些相应的地区
- 放弃这个属性
- 将缺失值设置为某个值(0、平均数或者中位数等)
通过DataFrame的dropna()、drop()和fillna()方法,可以轻松完成这些操作:
# #选择1
# data.dropna(subset=["total_bedrooms"])
# #选择2
# data.drop("total_bedrooms", axis=1)
#选择3
median = data["total_bedrooms"].median()
data["total_bedrooms"].fillna(median)运行结果如下:
17606 351.0
18632 108.0
14650 471.0
3230 371.0
3555 1525.0
...
6563 236.0
12053 294.0
13908 872.0
11159 380.0
15775 682.0
Name: total_bedrooms, Length: 16512, dtype: float64选择3中我们使用训练集的中位数值来填充训练集中的缺失值。
Scikit-Leam提供了一个非常容易上手的教程来处理缺失值:imputer。使用方法如下, 首先,我们需要创建一个imputer实例,指定我们要用属性的中位数值替换该属性的缺失值:
缺失值处理:SimpleImputer(简单易懂 + 超详细)_Dream丶Killer的博客-CSDN博客_simpleimputer
from sklearn.preprocessing import Imputer/from sklearn.cross_validation import train_test_split报错_才疏学浅的才学的博客-CSDN博客
(此处可参考这2篇博文讲解)
Simpleimputer参数详解:
imputer = SimpleImputer(missing_values = np.nan, strategy = "mean",
fill_value=None, verbose=0, copy=True,
add_indicator=False)
# missing_values:int, float, str, (默认)np.nan或是None, 即缺失值是什么。
# strategy:空值填充的四种选择(默认)mean、median、most_frequent、constant;mean表示该列的缺失值由该列的均值填充;median为中位数,most_frequent为众数。constant表示将空值填充为自定义的值,但这个自定义的值要通过fill_value来定义。
# fill_value:str或数值,默认为Zone。当strategy == "constant"时,fill_value被用来替换所有出现的缺失值(missing_values)。fill_value为Zone,当处理的是数值数据时,缺失值(missing_values)会替换为0,对于字符串或对象数据类型则替换为"missing_value" 这一字符串。
# verbose:int,(默认)0,控制imputer的冗长。
# copy:boolean,(默认)True,表示对数据的副本进行处理,False对数据原地修改。
# add_indicator:boolean,(默认)False,True则会在数据后面加入n列由0和1构成的同样大小的数据,0表示所在位置非缺失值,1表示所在位置为缺失值。from sklearn.impute import SimpleImputer
imputer = SimpleImputer(strategy="median")
#由于中位数值只能在数值属性上计算,因此我们需要创建一个没有文本属性的数据副本ocean_proximity
data_num = data.drop("ocean_proximity", axis=1)
#使用fit()方法将imputer实例适配到训练集:
imputer.fit(data_num)这里imputer仅仅只是计算了每个属性的中位数值,并将结果存储在其实例变量statistics_中虽然只有total_bedrooms这个属性存在缺失值,但是我们无法确认系统启动之后新数据中是否一定不存在任何缺失值,所以稳妥起见,还是将imputer应用于所有的数值属性:
imputer.statistics_运行结果如下:
array([-118.51 , 34.26 , 29. , 2119.5 , 433. , 1164. ,
408. , 3.5409])data_num.median().values运行结果如下:
array([-118.51 , 34.26 , 29. , 2119.5 , 433. , 1164. ,
408. , 3.5409])使用imputer将缺失值替换成中位数值完成训练集转换:
X = imputer.transform(data_num)结果是一个包含转换后特征的Numpy数组。如果想要将它放回Pandas DataFrame, 也很简单:
#data_tr = pd.DataFrame(X, columns = housing_num.columns)6.2 处理文本和分类属性
之前我们排除了分类属性ocean_proximity,因为它是一个文本属性,我们无法计算它的中位数的值。大部分的机器学习算法都更易于跟数字打交道,所以我们先将这些文本标签转化为数字。
Scikit-Learn为这类任务提供了一个转换器LabelEncoder:
from sklearn.preprocessing import LabelEncoder
encoder = LabelEncoder()
data_cat = data["ocean_proximity"]
data_cat_encoded = encoder.fit_transform(data_cat)
data_cat_encoded运行结果如下:
array([0, 0, 4, ..., 1, 0, 3])我们可以使用classes_属性来查看这个编码器已学习的映射(“<1H OCEAN” 对应为0, “INLAND”对应为1, 等等):
print(encoder.classes_)运行结果如下:
['<1H OCEAN' 'INLAND' 'ISLAND' 'NEAR BAY' 'NEAR OCEAN']这种代表方式产生的一个问题是,机器学习算法会以为两个相近的数字比两个离得较远的数字更为相似一些。显然,真实情况并非如此(比如,类别0和类别4之间就比类别0和类别1之间的相似度更高)。为了解决这个问题,常见的解决方案是给每个类别创建一个二进制的属性:当类别是“<1H OCEAN”时,一个属性为1(其他为0),当类别 是“INLAND”时,另一个属性为1(其他为0),以此类推。这就是独热编码,因为只有一个属性为1(热),其他均为0(冷)。
Scikit-Learn 提供了一个 OneHotEncoder编码器,可以将整数分类值转换为独热向量。我们用它来将类别编码为独热向量。值得注意的是, fit_transform()需要一个二维数组,但是housing_cat_encoded是一个一维数组,所以我们需要将它重塑:
from sklearn.preprocessing import OneHotEncoder
encoder = OneHotEncoder()
data_cat_1hot = encoder.fit_transform(data_cat_encoded.reshape(-1,1))
data_cat_1hot运行结果如下:
<16512x5 sparse matrix of type ''
with 16512 stored elements in Compressed Sparse Row format> 注意到这里的输出是一个SciPy稀疏矩阵,而不是一个NumPy数组。当你有成千上万种类别的分类属性时,这个函数会非常有用。因为当独热编码完成之后,我们会得到一个几千列的矩阵,并且全是0,每行仅有一个1。占用大量内存来存储0是一件非常浪费的事情,因此稀疏矩阵选择仅存储非零元素的位置。而你依旧可以像使用一个普通的二维数组那样来使用它。当然如果你实在想把它转换成一个(密集的) NumPy数组, 只需要调用 toarray()方法即可:
data_cat_1hot.toarray()运行结果如下:
array([[1., 0., 0., 0., 0.],
[1., 0., 0., 0., 0.],
[0., 0., 0., 0., 1.],
...,
[0., 1., 0., 0., 0.],
[1., 0., 0., 0., 0.],
[0., 0., 0., 1., 0.]])使用LabelBinarizer类可以一次性完成两个转换(从文本类别转化为整数类别,再从整数类别转换为独热向量):
from sklearn.preprocessing import LabelBinarizer
encoder = LabelBinarizer()
data_cat_1hot = encoder.fit_transform(data_cat)
data_cat_1hot运行结果如下:
array([[1, 0, 0, 0, 0],
[1, 0, 0, 0, 0],
[0, 0, 0, 0, 1],
...,
[0, 1, 0, 0, 0],
[1, 0, 0, 0, 0],
[0, 0, 0, 1, 0]])注意,这时默认返回的是一个密集的NumPy数组。通过发送sparse_output=True给LabelBinarizer构造函数,可以得到稀疏矩阵。
from sklearn.preprocessing import LabelBinarizer
encoder = LabelBinarizer(sparse_output=True)
data_cat_1hot = encoder.fit_transform(data_cat)
data_cat_1hot运行结果如下:
<16512x5 sparse matrix of type ''
with 16512 stored elements in Compressed Sparse Row format> 6.3 自定义转换器
虽然Scikit-Learn已经提供了许多有用的转换器,但是我们仍然需要为一些诸如自定义清理操作或是组合特定属性等任务编写自己的转换器。当然我们希望让自己的转换器与Scikit-Learn自身的功能(比如流水线)无缝衔接,而由于Scikit-Learn依赖于鸭子类型(duck typing)的编译,而不是继承,所以我们所需要的只是创建一个类,然后应用以下三个方法: fit()(返回自身)、transform()、fit_transform()。如果添加TransformerMixin作为基类,就可以直接得到最后一个方法。同时,如果添加 BaseEstimator作为基类(并在构造函数中避免*args和**kargs),还能额外获得两个非常有用的自动调整超参数的方法(get_params()和set_params())。例如,我们前面讨论过的组合属性,这里有个简单的转换器类,用来添加组合后的属性:
from sklearn.base import BaseEstimator, TransformerMixin
rooms_ix, bedrooms_ix, population_ix, household_ix = 3, 4, 5, 6
class CombinedAttributesAdder(BaseEstimator, TransformerMixin):
def __init__(self, add_bedrooms_per_room = True): # no *args or **kargs
self.add_bedrooms_per_room = add_bedrooms_per_room
def fit(self, X, y=None):
return self # nothing else to do
def transform(self, X, y=None):
rooms_per_household = X[:, rooms_ix] / X[:, household_ix]
population_per_household = X[:, population_ix] / X[:, household_ix]
if self.add_bedrooms_per_room:
bedrooms_per_room = X[:, bedrooms_ix] / X[:, rooms_ix]
return np.c_[X, rooms_per_household, population_per_household,
bedrooms_per_room]
else:
return np.c_[X, rooms_per_household, population_per_household]
attr_adder = CombinedAttributesAdder(add_bedrooms_per_room=False)
data_extra_attribs = attr_adder.transform(data.values)在本例中,转换器有一个超参数add_bedrooms_per_room默认设置为True (提供合理的默认值通常是很有帮助的)。这个超参数可以让我们轻松知晓添加这个属性是否有助于机器学习的算法。更广泛地说,如果我们对数据准备的步骤没有充分的信心,就可以添加这个超参数来进行把关。这些数据准备步骤的执行越自动化,我们自动尝试的组合也就越多,从而有更大可能从中找到一个重要的组合(还节省了大量时间)。
6.4 特征缩放
最重要也最需要应用到数据上的转换器,就是特征缩放。如果输入的数值属性具有非常大的比例差异,往往导致机器学习算法的性能表现不佳,当然也有极少数特例。案例中的房屋数据就是这样:房间总数的范围从6到39320,而收入中位数的范围是0到15。注意,目标值通常不需要缩放。
同比例缩放所有属性,常用的两种方法是:最小-最大缩放和标准化。
最小-最大缩放(又叫作归一化)很简单:将值重新缩放使其最终范围归于0到1之间。实现方法是将值减去最小值并除以最大值和最小值的差。对此,Scikit-Learn提供了一个名为MinMaxScaler的转换器。如果出于某种原因,你希望范围不是0~1,你可以通过调整超参数feature_range进行更改。
标准化则完全不一样:首先减去平均值(所以标准化值的均值总是零),然后除以方差,从而使得结果的分布具备单位方差。不同于最小-最大缩放的是,标准化不将值绑定到特定范围,对某些算法而言,这可能是个问题(例如,神经网络期望的输入值范围通常是0到1)。但是标准化的方法受异常值的影响更小。例如,假设某个地区的平均收入等于100(错误数据)。最小-最大缩放会将所有其他值从0~15降到0~0.15,而标准化则不会受到很大影响。Scikit-Learn提供了一个标准化的转换器 StandadScaler。
6.5 转换流水线
正如你所见,许多数据转换的步骤需要以正确的顺序来执行。而Scikit-Learn正好提供了Pipeline来支持这样的转换。下面是一个数值属性的流水线例子:
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
num_pipeline = Pipeline([
('imputer', SimpleImputer(strategy="median")),
('attribs_adder', CombinedAttributesAdder())
('std_scaler', StandardScaler())])
data_num_tr = num_pipeline.fit_transform(data_num)Pipeline构造函数会通过一系列名称/估算器的配对来定义步骤的序列。除了最后一个是估算器之外,前面都必须是转换器(也就是说,必须有fit_transform()方法)。
当调用流水线的fit()方法时,会在所有转换器上按照顺序依次调用fit_transform(),将一个调用的输出作为参数传递给下一个调用方法,直到传递到最终的估算器,则只会调用fit()方法。
流水线的方法与最终的估算器的方法相同。在本例中,最后一个估算器是StandardScaler, 这是个转换器,因此Pipeline有transform()方法可以按顺序将所有的转换应用到数据中(如果不希望先调用fit()再调用 transform(),也可以直接调用 fit_transform()方法)。
现在,我们已经有了一个处理数值的流水线,接下来需要在分类值上应用LabelBinarizer:不然怎么将这些转换加人单个流水线中? Scikit-Learn为此特意提供了一个FeatureUnion类。我们只需要提供一个转换器列表(可以是整个转换器流水线),当transform()方法被调用时,它会并行运行每个转换器的transform()方法,等待它们的输出,然后将它们连结起来,返回结果(同样地,调用fit()方法也会调用每个转换器的fit()方法)。一个完整的处理数值和分类属性的流水线可能如下所示:
2022.8.9持续补充中······
学习笔记——《机器学习实战:基于Scikit-Learn和TensorFlow》