Siamese network

一、相似性度量

  相似性度量是机器学习中一个非常基础的概念，是评定两个事物之间相似程度的一种度量，尤其是在聚类、推荐算法中尤为重要。其本质就是一种量化标准，即对象间越相似，相似度越大，距离越小（度量值越小），对象间越不相似，相似度越小，距离越大（度量值越大）。
  下面介绍几种常见的相似性度量函数。

1. 欧氏距离

  欧氏距离也称欧几里得距离，是最常见的距离度量，衡量的是多维空间中两个点之间的绝对距离。计算公式如下：

  但是，欧氏距离在多维数据的场景下，还存在以下局限性：
  (a) 如果各分量的单位不全相同，则上述欧氏距离是不准确的。例如，第一个分量的单位是kg，第二个分量的单位是g，这意味着所计算的距离可能会根据特征的单位发生倾斜。
  (b) 即使单位相同，但如果各分量的变异性差异很大，则变异性大的分量在欧氏距离的平方和中起着决定性的作用，而变异性小的分量却几乎不起什么作用。
  一种常见的解决方案是对各分量都做标准化处理，则各分量方差同为1且均值为0，于是，平方和中各分量所起的平均作用都一样，即使单位不同，计算结果也不受其影响。

2. 马氏距离

  欧氏距离经分量的标准化之后能够消除各分量的单位或方差差异的影响，但不能消除分量之间相关性的影响。
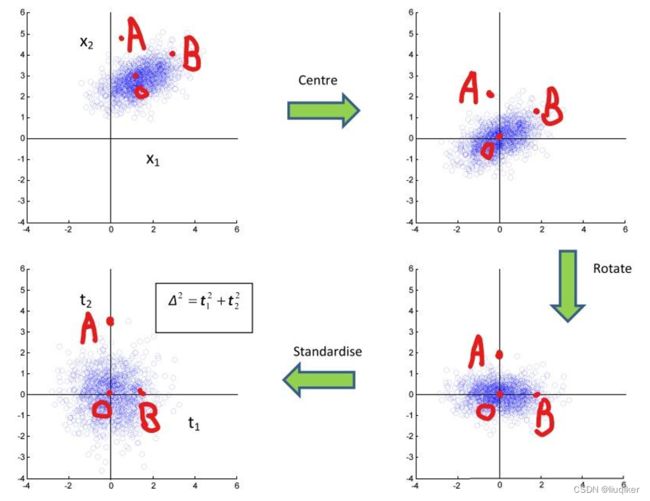
  如下图（左上）所示，蓝点是某二维数据集分布，可以看出此数据集的x,y两个维度非独立同分布，有相关性（类似y=x）。O可以认为是数据集的中心。请问A点和B点哪个距离这个数据集更近（或者说相似度更高）？直觉上肯定是觉得B点更近，B相较于A更可能是数据集中的一个点。但若采用欧拉距离计算，AO和BO的数值是一样的，因此，显然不能用一般的距离计算公式来计算。而且标准化并不能改变数据的分布，对距离的计算并没有什么帮助。
  这种情况下，采用马氏距离，便可得出A到O的距离大于B到O的距离，下图直观的展示了马氏距离的计算过程：

  马氏距离公式如下，表示的是两个服从同一分布并且其协方差矩阵为Σ的随机变量X与Y的差异程度。

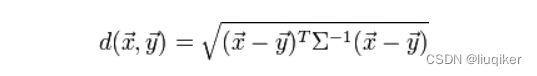
  对于变量a和b，协方差表示a和b之间的关系（协方差大于0，a和b正相关；协方差小于，a和b负相关；协方差等于0，a和b不相关）。
  而马氏距离的目的，就是计算所有分量不相关后两个变量间的差异，而令所有分量不相关的方法，便是公式中的协方差矩阵（即上上图的“旋转”过程）。

二、Siamese network

  Siamese Network（孪生网络）也称为“连体的神经网络”，是一种用于度量学习的监督模型，主要用于衡量两个输入的相似程度。

1. Siamese network 基础架构

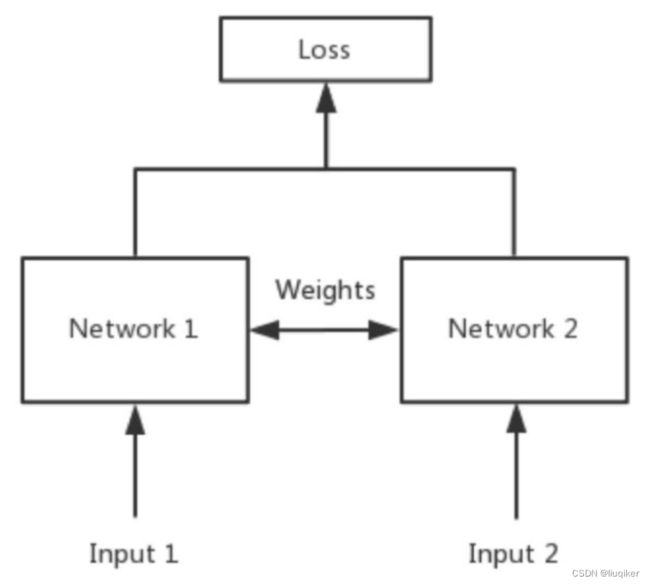
  下图是Siamese network的基础架构，其中Input 1和Input 2是需要比较相似度的输入，它们通过两个具有相同架构、参数和权重的相似子网络（Network 1和Network 2）并输出特征编码，最终经过损失函数（Loss）的计算，得到两个输入的相似度量。
  需要注意的是，这里的两个子网络是共享权重（Weights）的，不共享权重的孪生网络又叫伪孪生网络，这里不做讨论。

  如下是基于TensorFlow实现的简单Siamese network模型，主要功能是识别两张28×28图片的相似度。其中Network 1和Network 2实现为简单神经网络，在真正的应用过程中，需要视情况替换为CNN模型。

# 单个神经网络，对应基础架构图中的Network 1和2
def initialize_base_network():
	input = Input(shape=(28, 28, ), name="base_input")
	x = Flatten(name="flatten_input")(input)
	x = Dense(128, activation='relu', name="first_base_dense")(x)
	x = Dropout(0.1, name="first_dropout")(x) # 防止过拟合
	x = Dense(128, activation='relu', name="second_base_dense")(x)
	x = Dropout(0.1, name="second_dropout")(x)
	x = Dense(128, activation='relu', name="third_base_dense")(x)
	return Model(inputs=input, outputs=x)

# Loss函数使用欧氏距离
def euclidean_distance(vects):
	x, y = vects
	sum_square = K.sum(K.square(x - y), axis=1, keepdims=True)
	return K.sqrt(K.maximum(sum_square, K.epsilon()))

# 输出格式
def eucl_dist_output_shape(shapes):
	shape1, shape2 = shapes
	return (shape1[0], 1)

# 构建Siamese network
base_network = initialize_base_network() # 目的是共享权重和模型，即两个输入进入同一个神经网络训练
input_1 = Input(shape=(28, 28, ), name="Network_1")
vect_output_1 = base_network(input_1) # base_network为model，此处会调用model.__call__()
input_2 = Input(shape=(28, 28, ), name="Network_2")
vect_output_2 = base_network(input_2)

output = Lambda(euclidean_distance, name="output_layer", output_shape=eucl_dist_output_shape)([vect_output_1, vect_output_2])

model = Model([input_1, input_2], output)

  模型构建结果如下，最上层为需要比较相似度的两个输入，经过完全相同且共享权重的简单神经网络，最后经过欧氏距离计算输出度量值。

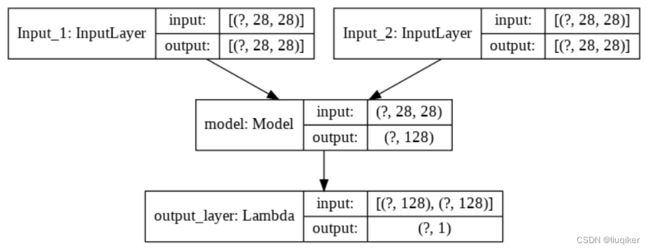
2. 损失函数

  在训练Siamese network时，容易犯的一个错误是只输入“属于同一类的”两个图片（正样本），这样训练的模型，将无法分辨“不是同一类的”图片（负样本）。
  因此我们需要同时训练正样本和负样本，而损失函数的作用，则是要让正样本的损失尽量小，而负样本的损失尽量大，设计思路如下：

  几种常见的损失函数有：

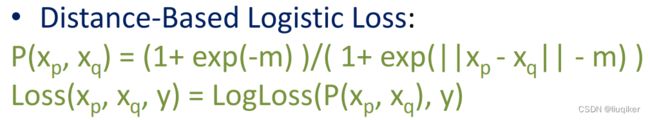
3. 不同的Siamese network

3.1. 行人重识别

  行人重识别（Person Re-identification，也称行人再识别，简称为ReID），是利用计算机视觉技术判断图像或者视频序列中是否存在特定行人的技术。
  在监控视频中，由于相机分辨率和拍摄角度的缘故，通常无法得到质量非常高的人脸图片。当人脸识别失效的情况下，ReID就成为了一个非常重要的替代品技术。如下图所示，在一系列视频截图中识别出属于同一个人的图片。

  一个解决上述问题的Siamese network模型（2015 CVPR-An Improved Deep Learning Architecture for Person Re-Identification）如下：


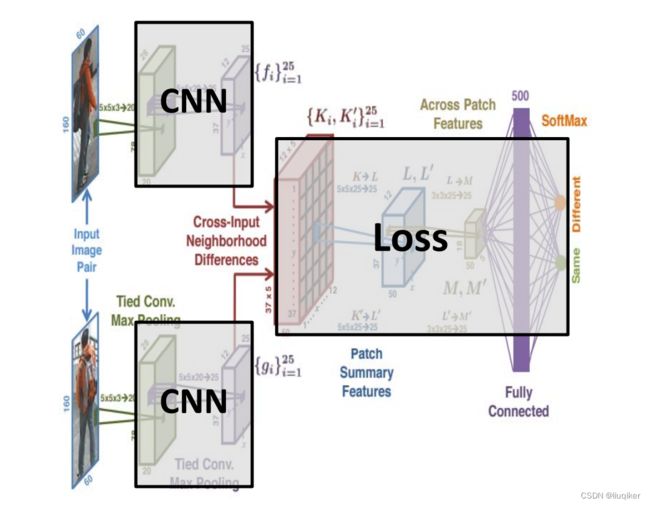
  图中两个conv-maxpooling层来对图像对提取特征（论文里称为higher-order features）；Cross-Input Neighborhood Differences层是用来对前层输出计算对应两个特征图的邻域差异（neightborhood difference）；Patch Summary Features层对每个上层输出中的每个5x5块进行求和来得到整体的差异；Across-Patch Features层L，L′分别使用25个3x3x25、步长为1的卷积核学习neighborhood differences之间的空间关系；最后通过全连接层来捕获高层次的关系，再通过一层两个带softmax节点的全连接得到最终输出。

3.2 其他应用场景

  Siamese network的应用场景还包括：街景图和俯视图匹配、图像和文字匹配、句子和句子相似度比较等，在此不再详细介绍。