ch03-PyTorch模型搭建

0.引言

1.模型创建步骤与 nn.Module

前几节中，我们学习了 PyTorch 的数据模块，并了解了 PyTorch 如何从硬盘中读取数据，然后对数据进行预处理、数据增强，最后转换为张量的形式输入到我们的模型中。在深度模型中，会对张量进行一系列复杂的数学运算，最终得到用于分类、分割、目标检测等任务的输入。本节中，我们将学习 PyTorch 中模型的创建以及 nn.Module 的相关概念。

1.1. 网络模型的创建步骤

在学习创建模型之前，我们先回顾一下之前提到的机器学习模型训练的 5 个步骤：

我们已经在前几节课中完成了对数据模块的学习，接下来我们开始学习模型模块。

回顾一下之前在人民币分类的例子中我们使用过的 LeNet 网络：

LeNet 模型结构图：

可以看到，LeNet 网络由 7 个层构成：卷积层 1、池化层 1、卷积层 2、池化层 2，以及 3 个全连接层。在创建 LeNet 时，需要先构建这些子模块，在构建完成这 7 个子网络层后，我们会采用一定的顺序对其进行连接。最后，将它们包装起来就得到我们的 LeNet 网络。

在 PyTorch 中，LeNet 是一个 Module 的概念，而它的子网络层也是一个 Module 的概念，它们都属于 nn.Module 类。所以，一个 nn.Module (例如：LeNet) 可以包含很多个子 Module (例如：卷积层、池化层等)。

下面我们从计算图的角度来观察模型的创建过程：

计算图中有两个主要的概念：结点和边。其中，结点代表张量 (数据)，边代表运算。LeNet 整体上可以视为一组张量运算：它接收一个 32*32*3 的张量，经过一系列复杂运算之后，输出一个长度为 10 的向量作为分类概率。而在 LeNet 内部，则由一系列子网络层构成，例如：卷积层 1 对一个 32*32*3 的张量进行卷积操作得到一个 28*28*6 的张量，并将其作为下一层子网络的输入，经过这种不断的前向传播，最终计算得到输出概率。在深度学习中，该过程被称为 前向传播。

我们从网络结构和计算图的角度分析了 LeNet 网络模型，并且知道了构建模型的两个要素：构建子模块和拼接子模块。

接下来，我们还是通过之前人民币二分类的例子来学习如何构建模型。以 lenet.py 的 LeNet 为例，继承nn.Module，必须实现__init__() 方法和forward()方法。其中__init__() 方法里创建子模块，在 forward() 方法里拼接子模块。

构建模型：

# ============================ step 2/5 模型 ============================
net = LeNet(classes=2)
net.initialize_weights()

LeNet 类：

class LeNet(nn.Module):
    # 构建子模块
    def __init__(self, classes):
        super(LeNet, self).__init__()
        self.conv1 = nn.Conv2d(3, 6, 5)
        self.conv2 = nn.Conv2d(6, 16, 5)
        self.fc1 = nn.Linear(16*5*5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, classes)

    # 拼接子模块
    def forward(self, x):
        out = F.relu(self.conv1(x))
        out = F.max_pool2d(out, 2)
        out = F.relu(self.conv2(out))
        out = F.max_pool2d(out, 2)
        out = out.view(out.size(0), -1)
        out = F.relu(self.fc1(out))
        out = F.relu(self.fc2(out))
        out = self.fc3(out)
        return out

    def initialize_weights(self):
        for m in self.modules():
            if isinstance(m, nn.Conv2d):
                nn.init.xavier_normal_(m.weight.data)
                if m.bias is not None:
                    m.bias.data.zero_()
            elif isinstance(m, nn.BatchNorm2d):
                m.weight.data.fill_(1)
                m.bias.data.zero_()
            elif isinstance(m, nn.Linear):
                nn.init.normal_(m.weight.data, 0, 0.1)
                m.bias.data.zero_()

当我们调用 net = LeNet(classes=2) 创建模型时，会调用 __init__() 方法创建模型的子模块。

当我们在训练时调用 outputs = net(inputs) 时，会进入 module.py（LeNet的父类）的call()函数中：

    def __call__(self, *input, **kwargs):
        for hook in self._forward_pre_hooks.values():
            result = hook(self, input)
            if result is not None:
                if not isinstance(result, tuple):
                    result = (result,)
                input = result
        if torch._C._get_tracing_state():
            result = self._slow_forward(*input, **kwargs)
        else:
            result = self.forward(*input, **kwargs)
        ...
        ...
        ...

最终会调用 result = self.forward(*input, **kwargs) 函数，该函数会进入模型的 forward() 函数中，进行前向传播。

在 torch.nn中包含 4 个模块，如下图所示。

其中所有网络模型都是继承于nn.Module的，下面重点分析nn.Module模块。

1.2. nn.Module

在模型模块中，我们有一个非常重要的概念 —— nn.Module。我们所有的模型和网络层都是继承自 nn.Module 这个类的，所以我们有必要了解它。在学习 nn.Module 之前，我们先来看一下与其相关的几个模块：

首先是 torch.nn，它是 PyTorch 的一个神经网络模块，其中又有很多子模块，这里我们需要了解其中的 4 个模块：nn.Parameter、nn.Module、nn.functional 和 nn.init。本节课我们先重点关注 nn.Module。

• nn.Module

在 nn.Module 中有 8 个重要的属性，用于管理整个模型：

nn.Module 有 8 个属性，用于管理整个模型，都是 OrderDict (有序字典)。在 LeNet 的 __init__() 方法中会调用父类 nn.Module 的 __init__() 方法，创建这 8 个属性。

self._parameters = OrderedDict()
self._buffers = OrderedDict()
self._backward_hooks = OrderedDict()
self._forward_hooks = OrderedDict()
self._forward_pre_hooks = OrderedDict()
self._state_dict_hooks = OrderedDict()
self._load_state_dict_pre_hooks = OrderedDict()
self._modules = OrderedDict()

主要了解属性：

• parameters：存储管理 nn.Parameter 类。
• modules：存储管理 nn.Module 类（子模型）。
• buffers：存储管理缓冲属性，如 BN 层中的 running_mean。
• ***_hooks：存储管理钩子函数。

这里，我们重点关注其中的两个属性：parameters 和 modules。

在 LeNet 的 __init__() 中创建了 5 个子模块，nn.Conv2d() 和 nn.Linear() 都是 继承于 nn.module ，也就是说一个 module 都是包含多个子 module 的。

class LeNet(nn.Module):
	# 子模块创建
    def __init__(self, classes):
        super(LeNet, self).__init__()
        self.conv1 = nn.Conv2d(3, 6, 5)
        self.conv2 = nn.Conv2d(6, 16, 5)
        self.fc1 = nn.Linear(16*5*5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, classes)
        ...
        ...
        ...

当调用net = LeNet(classes=2)创建模型后，net对象的 modules 属性就包含了这 5 个子网络模块。

下面看下每个子模块是如何添加到 LeNet 的_modules 属性中的。以self.conv1 = nn.Conv2d(3, 6, 5)为例，当我们运行到这一行时，首先 Step Into 进入 Conv2d的构造，然后 Step Out。右键Evaluate Expression查看nn.Conv2d(3, 6, 5)的属性。

上面说了Conv2d也是一个 module，里面的_modules属性为空，_parameters属性里包含了该卷积层的可学习参数，这些参数的类型是 Parameter，继承自 Tensor。

此时只是完成了nn.Conv2d(3, 6, 5) module 的创建。还没有赋值给self.conv1 。在nn.Module里有一个机制，会拦截所有的类属性赋值操作(self.conv1是类属性)，进入到__setattr__()函数中。我们再次 Step Into 就可以进入__setattr__()。

 def __setattr__(self, name, value):
        def remove_from(*dicts):
            for d in dicts:
                if name in d:
                    del d[name]

        params = self.__dict__.get('_parameters')
        if isinstance(value, Parameter):
            if params is None:
                raise AttributeError(
                    "cannot assign parameters before Module.__init__() call")
            remove_from(self.__dict__, self._buffers, self._modules)
            self.register_parameter(name, value)
        elif params is not None and name in params:
            if value is not None:
                raise TypeError("cannot assign '{}' as parameter '{}' "
                                "(torch.nn.Parameter or None expected)"
                                .format(torch.typename(value), name))
            self.register_parameter(name, value)
        else:
            modules = self.__dict__.get('_modules')
            if isinstance(value, Module):
                if modules is None:
                    raise AttributeError(
                        "cannot assign module before Module.__init__() call")
                remove_from(self.__dict__, self._parameters, self._buffers)
                modules[name] = value
            elif modules is not None and name in modules:
                if value is not None:
                    raise TypeError("cannot assign '{}' as child module '{}' "
                                    "(torch.nn.Module or None expected)"
                                    .format(torch.typename(value), name))
                modules[name] = value
            ...
            ...
            ...

在这里判断 value 的类型是Parameter还是Module，存储到对应的有序字典中。

这里nn.Conv2d(3, 6, 5)的类型是Module，因此会执行modules[name] = value，key 是类属性的名字conv1，value 就是nn.Conv2d(3, 6, 5)。

---

nn.Module 的属性构建机制： 在 module 类里面进行属性赋值时会先被 setattr 函数拦截，该函数对即将赋值的数据类型进行判断：

• 如果赋值是 nn.Parameter 类，则将其存入 parameters 字典中进行管理；
• 如果赋值是 nn.Module 类，则将其存入 modules 字典中进行管理。

nn.Module 总结：

• 一个 module 可以包含多个子 module。
  • 例如：在 LeNet 这个 module 下会包含一些卷积层、池化层等子 module。
• 一个 module 相当于一个运算，必须实现 forward() 函数。
  • 从计算图的角度来看，一个 module 接收一个张量，经过一系列复杂运算，输出概率或者其他数据。因此，我们需要在其中实现一个前向传播的函数。
• 每个 module 都有 8 个 有序字典 (OrderedDict) 管理它的属性。
  • 这里，最常用的是 parameters 字典和 modules 字典。

1.3. 总结

本节中，我们学习了 nn.Module 的概念以及模型创建的两个要素。下节中，我们将学习容器 Containers 以及 AlexNet 的搭建。

2.模型容器与 AlexNet 构建

上节中，我们学习了如何搭建一个模型，搭建模型的过程中有两个要素：构建子模块和拼接子模块。另外，搭建模型时还有一个非常重要的概念：模型容器 (Containers)。本节课我们将学习模型容器以及 AlexNet 的构建。

2.1. 模型容器

除了上述的模块之外，还有一个重要的概念是模型容器 (Containers)，常用的容器有 3 个，这些容器都是继承自nn.Module。

• nn.Sequetial：按照顺序包装多个网络层
• nn.ModuleList：像 python 的 list 一样包装多个网络层，可以迭代
• nn.ModuleDict：像 python 的 dict 一样包装多个网络层，通过 (key, value) 的方式为每个网络层指定名称。

2.1.1.nn.Sequential

• nn.Sequential 是 nn.Module 的容器，用于 按顺序 包装一组网络层。

在传统的机器学习中，有一个步骤是特征工程，我们需要从数据中认为地提取特征，然后把特征输入到分类器中预测。在深度学习的时代，特征工程的概念被弱化了，特征提取和分类器这两步被融合到了一个神经网络中。在卷积神经网络中，前面的卷积层以及池化层可以认为是特征提取部分，而后面的全连接层可以认为是分类器部分。比如 LeNet 就可以分为特征提取和分类器两部分，这 2 部分都可以分别使用 nn.Seuqtial 来包装。

nn.Sequential 将一组网络层按顺序包装为一个整体，可以视为模型的一个子模块。在传统的机器学习中有一个步骤被称为特征工程：我们需要人为地设计特征，并将特征输入到分类器当中进行分类。在深度学习时代，特征工程这一概念已经被弱化，尤其是在卷积神经网络中，我们不需要人为设计图像特征，相反，我们可以让卷积神经网络去自动学习特征，并在最后加上几个全连接层用于输出分类结果。在早期的神经网络当中，用于分类的分类器是由全连接构成的，所以在深度学习时代，通常也习惯以全连接层为界限，将网络模型划分为特征提取模块和分类模块。对一个大的模型进行划分可以方便按照模块进行管理：例如在上面的 LeNet 模型中，我们可以将多个卷积层和池化层包装为一个特征提取器，并且将后面的几个全连接层包装为一个分类器，最后再将这两个模块包装为一个完整的 LeNet 神经网络。在 PyTorch 中，我们可以使用 nn.Sequential 完成这些包装过程。

代码示例：

class LeNetSequential(nn.Module):
    def __init__(self, classes):
        super(LeNetSequential, self).__init__()

        self.features = nn.Sequential(
            nn.Conv2d(3, 6, 5),
            nn.ReLU(),
            nn.MaxPool2d(kernel_size=2, stride=2),
            nn.Conv2d(6, 16, 5),
            nn.ReLU(),
            nn.MaxPool2d(kernel_size=2, stride=2),)

        self.classifier = nn.Sequential(
            nn.Linear(16*5*5, 120),
            nn.ReLU(),
            nn.Linear(120, 84),
            nn.ReLU(),
            nn.Linear(84, classes),)

    def forward(self, x):
        x = self.features(x)
        x = x.view(x.size()[0], -1)
        x = self.classifier(x)
        return x
 
    net = LeNetSequential(classes=2)

    fake_img = torch.randn((4, 3, 32, 32), dtype=torch.float32)

    output = net(fake_img)

    print(net)
    print(output)        

输出：

LeNetSequetial(
  (features): Sequential(
    (0): Conv2d(3, 6, kernel_size=(5, 5), stride=(1, 1))
    (1): ReLU()
    (2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
    (3): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
    (4): ReLU()
    (5): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  )
  (classifier): Sequential(
    (0): Linear(in_features=400, out_features=120, bias=True)
    (1): ReLU()
    (2): Linear(in_features=120, out_features=84, bias=True)
    (3): ReLU()
    (4): Linear(in_features=84, out_features=2, bias=True)
  )
)
tensor([[0.0413, 0.0061],
        [0.0484, 0.0132],
        [0.0089, 0.0006],
        [0.0297, 0.0040]], grad_fn=<AddmmBackward0>)

---

分析一下这个网络：

给定的输入是一个尺寸为 (4, 3, 32, 32) 的假图像张量，其中 4 代表批量大小，3 代表图像通道数（RGB），32x32 代表图像的宽度和高度。

1.第一卷积层（nn.Conv2d(3, 6, 5)）：

• 输入：(4, 3, 32, 32)
• 输出：(4, 6, 28, 28)。输出通道为 6，卷积核大小为 5x5，没有填充，因此 (32 - 5 + 1)/1 = 28。
• 参数维度：(6, 3, 5, 5)，其中6个输出通道，3个输入通道，5x5的卷积核。参数是共享的。

2.ReLU激活函数：

• 输入：(4, 6, 28, 28)
• 输出：(4, 6, 28, 28)。ReLU 不改变输入的维度。
• 无参数。

3.最大池化层（nn.MaxPool2d(kernel_size=2, stride=2)）：

• 输入：(4, 6, 28, 28)
• 输出：(4, 6, 14, 14)。池化层将输入的宽度和高度减半。
• 无参数。

4.第二卷积层（nn.Conv2d(6, 16, 5)）：

• 输入：(4, 6, 14, 14)
• 输出：(4, 16, 10, 10)。输出通道为 16，卷积核大小为 5x5，没有填充，因此 (14 - 5 + 1)/1=10。
• 参数维度：(16, 6, 5, 5)，其中16个输出通道，6个输入通道，5x5的卷积核。参数是共享的。

5.ReLU激活函数：

• 输入：(4, 16, 10, 10)
• 输出：(4, 16, 10, 10)。ReLU 不改变输入的维度。
• 无参数。

6.最大池化层（nn.MaxPool2d(kernel_size=2, stride=2)）：

• 输入：(4, 16, 10, 10)
• 输出：(4, 16, 5, 5)。池化层将输入的宽度和高度减半。
• 无参数。

7.将输出展平：展平输出以将其输入到全连接层。

• 输入：(4, 16, 5, 5)
• 输出：(4, 400)。这里，16x5x5=400。

8.第一全连接层（nn.Linear(1655, 120)）：

• 输入：(4, 400)
• 输出：(4, 120)
• 参数维度：(120, 400)，其中120个输出节点，400个输入节点。

9.ReLU激活函数：

• 输入：(4, 120)
• 输出：(4, 120)。ReLU 不改变输入的维度。
• 无参数。

10.第二全连接层（nn.Linear(120, 84)）：

• 输入：(4, 120)
• 输出：(4, 84)
• 参数维度：(84, 120)，其中84个输出节点，120个输入节点。

11.ReLU激活函数：

• 输入：(4, 84)
• 输出：(4, 84)。ReLU 不改变输入的维度。
• 无参数。

12.第三全连接层（nn.Linear(84, classes)）：

• 输入：(4, 84)
• 输出：(4, 2)，其中 classes=2。
• 参数维度：(2, 84)，其中2个输出节点，84个输入节点。

最终，网络输出的维度为 (4, 2)，这意味着对于每个输入图像，我们得到一个大小为 2 的输出向量，这可以用于分类任务。本例中，输出的分类是二分类。LeNetSequential 模型中，有以下几层包含参数：

1.第一卷积层（nn.Conv2d(3, 6, 5)）：

• 参数维度：(6, 3, 5, 5)
• 参数数量：6 * 3 * 5 * 5 = 450

2.第二卷积层（nn.Conv2d(6, 16, 5)）：

• 参数维度：(16, 6, 5, 5)
• 参数数量：16 * 6 * 5 * 5 = 2400

3.第一全连接层（nn.Linear(1655, 120)）：

• 参数维度：(120, 400)
• 参数数量：120 * 400 = 48000

4.第二全连接层（nn.Linear(120, 84)）：

• 参数维度：(84, 120)
• 参数数量：84 * 120 = 10080

5.第三全连接层（nn.Linear(84, classes)）：

• 参数维度：(2, 84)，其中 classes=2。
• 参数数量：2 * 84 = 168

现在我们将所有层的参数数量加起来：
450 + 2400 + 48000 + 10080 + 168 = 61098

因此，整个 LeNetSequential 网络中需要学习的参数总数为 61,098 个。

---

在初始化时，nn.Sequetial会调用__init__()方法，将每一个子 module 添加到 自身的_modules属性中。这里可以看到，我们传入的参数可以是一个 list，或者一个 OrderDict。如果是一个 OrderDict，那么则使用 OrderDict 里的 key，否则使用数字作为 key (OrderDict 的情况会在下面提及)。

    def __init__(self, *args):
        super(Sequential, self).__init__()
        if len(args) == 1 and isinstance(args[0], OrderedDict):
            for key, module in args[0].items():
                self.add_module(key, module)
        else:
            for idx, module in enumerate(args):
                self.add_module(str(idx), module)

网络初始化完成后有两个子 module：features和classifier。

而features中的子 module 如下，每个网络层以序号作为 key：

在进行前向传播时，会进入 LeNet 的forward()函数，首先调用第一个Sequetial容器：self.features，由于self.features也是一个 module，因此会调用__call__()函数，里面调用

result = self.forward(*input, **kwargs)，进入nn.Seuqetial的forward()函数，在这里依次调用所有的 module。

    def forward(self, input):
        for module in self:
            input = module(input)
        return input

在上面可以看到在nn.Sequetial中，里面的每个子网络层 module 是使用序号来索引的，即使用数字来作为 key。一旦网络层增多，难以查找特定的网络层，这种情况可以使用 OrderDict (有序字典)。代码中使用

class LeNetSequentialOrderDict(nn.Module):
    def __init__(self, classes):
        super(LeNetSequentialOrderDict, self).__init__()

        self.features = nn.Sequential(OrderedDict({
            'conv1': nn.Conv2d(3, 6, 5),
            'relu1': nn.ReLU(inplace=True),
            'pool1': nn.MaxPool2d(kernel_size=2, stride=2),

            'conv2': nn.Conv2d(6, 16, 5),
            'relu2': nn.ReLU(inplace=True),
            'pool2': nn.MaxPool2d(kernel_size=2, stride=2),
        }))

        self.classifier = nn.Sequential(OrderedDict({
            'fc1': nn.Linear(16*5*5, 120),
            'relu3': nn.ReLU(),

            'fc2': nn.Linear(120, 84),
            'relu4': nn.ReLU(inplace=True),

            'fc3': nn.Linear(84, classes),
        }))

    def forward(self, x):
        x = self.features(x)
        x = x.view(x.size()[0], -1)
        x = self.classifier(x)
        return x


net = LeNetSequentialOrderDict(classes=2)
fake_img = torch.randn((4, 3, 32, 32), dtype=torch.float32)
output = net(fake_img)
print(net)
print(output)

输出：

LeNetSequentialOrderDict(
  (features): Sequential(
    (conv1): Conv2d(3, 6, kernel_size=(5, 5), stride=(1, 1))
    (relu1): ReLU(inplace=True)
    (pool1): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
    (conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
    (relu2): ReLU(inplace=True)
    (pool2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  )
  (classifier): Sequential(
    (fc1): Linear(in_features=400, out_features=120, bias=True)
    (relu3): ReLU()
    (fc2): Linear(in_features=120, out_features=84, bias=True)
    (relu4): ReLU(inplace=True)
    (fc3): Linear(in_features=84, out_features=2, bias=True)
  )
)
tensor([[ 0.0525, -0.0253],
        [ 0.0452, -0.0292],
        [ 0.0359, -0.0491],
        [ 0.0413, -0.0322]], grad_fn=<AddmmBackward0>)

nn.Sequetial是nn.Module的容器，用于按顺序包装一组网络层，有以下两个特性。

• 顺序性：各网络层之间严格按照顺序构建。
• 自带 forward()：自带的 forward 里，通过 for 循环依次执行前向传播运算。

2.1.2.nn.ModuleList

nn.ModuleList 是 nn.Module 的容器，用于包装一组网络层，以 迭代 方式调用网络层。主要有以下 3 个方法：

• append()：在 ModuleList 后面 添加 网络层。
• extend()：拼接 两个 ModuleList。
• insert()：指定在 ModuleList 中位置 插入 网络层。

下面的代码通过列表生成式来循环迭代创建 20 个全连接层，非常方便，只是在 forward()函数中需要手动调用每个网络层。代码示例：

class ModuleList(nn.Module):
    def __init__(self):
        super(ModuleList, self).__init__()
        # 构建 20 个全连接层
        self.linears = nn.ModuleList([nn.Linear(10, 10) for i in range(20)])

    def forward(self, x):
        for i, linear in enumerate(self.linears):
            x = linear(x)
        return x


net = ModuleList()
print(net)
fake_data = torch.ones((10, 10))
output = net(fake_data)
print(output)

输出：

ModuleList(
  (linears): ModuleList(
    (0): Linear(in_features=10, out_features=10, bias=True)
    (1): Linear(in_features=10, out_features=10, bias=True)
    (2): Linear(in_features=10, out_features=10, bias=True)
    (3): Linear(in_features=10, out_features=10, bias=True)
    (4): Linear(in_features=10, out_features=10, bias=True)
    (5): Linear(in_features=10, out_features=10, bias=True)
    (6): Linear(in_features=10, out_features=10, bias=True)
    (7): Linear(in_features=10, out_features=10, bias=True)
    (8): Linear(in_features=10, out_features=10, bias=True)
    (9): Linear(in_features=10, out_features=10, bias=True)
    (10): Linear(in_features=10, out_features=10, bias=True)
    (11): Linear(in_features=10, out_features=10, bias=True)
    (12): Linear(in_features=10, out_features=10, bias=True)
    (13): Linear(in_features=10, out_features=10, bias=True)
    (14): Linear(in_features=10, out_features=10, bias=True)
    (15): Linear(in_features=10, out_features=10, bias=True)
    (16): Linear(in_features=10, out_features=10, bias=True)
    (17): Linear(in_features=10, out_features=10, bias=True)
    (18): Linear(in_features=10, out_features=10, bias=True)
    (19): Linear(in_features=10, out_features=10, bias=True)
  )
)
tensor([[-0.3349, -0.0728, -0.3669,  0.2553, -0.1117,  0.1883,  0.3698,  0.1728,
         -0.2658, -0.0383],
        [-0.3349, -0.0728, -0.3669,  0.2553, -0.1117,  0.1883,  0.3698,  0.1728,
         -0.2658, -0.0383],
        [-0.3349, -0.0728, -0.3669,  0.2553, -0.1117,  0.1883,  0.3698,  0.1728,
         -0.2658, -0.0383],
        [-0.3349, -0.0728, -0.3669,  0.2553, -0.1117,  0.1883,  0.3698,  0.1728,
         -0.2658, -0.0383],
        [-0.3349, -0.0728, -0.3669,  0.2553, -0.1117,  0.1883,  0.3698,  0.1728,
         -0.2658, -0.0383],
        [-0.3349, -0.0728, -0.3669,  0.2553, -0.1117,  0.1883,  0.3698,  0.1728,
         -0.2658, -0.0383],
        [-0.3349, -0.0728, -0.3669,  0.2553, -0.1117,  0.1883,  0.3698,  0.1728,
         -0.2658, -0.0383],
        [-0.3349, -0.0728, -0.3669,  0.2553, -0.1117,  0.1883,  0.3698,  0.1728,
         -0.2658, -0.0383],
        [-0.3349, -0.0728, -0.3669,  0.2553, -0.1117,  0.1883,  0.3698,  0.1728,
         -0.2658, -0.0383],
        [-0.3349, -0.0728, -0.3669,  0.2553, -0.1117,  0.1883,  0.3698,  0.1728,
         -0.2658, -0.0383]], grad_fn=<AddmmBackward0>)

2.1.3.nn.ModuleDict

nn.ModuleDict 是 nn.Module 的容器，用于包装一组网络层，以 索引 方式调用网络层。主要方法：

• clear()：清空 ModuleDict。
• items()：返回可迭代的键值对 (key - value pairs)。
• keys()：返回字典的键 (key)。
• values()：返回字典的值 (value)。
• pop()：返回一对键值，并从字典中删除。

代码示例：

class ModuleDict(nn.Module):
    def __init__(self):
        super(ModuleDict, self).__init__()
        self.choices = nn.ModuleDict({
            'conv': nn.Conv2d(10, 10, 3),
            'pool': nn.MaxPool2d(3)
        })

        self.activations = nn.ModuleDict({
            'relu': nn.ReLU(),
            'prelu': nn.PReLU()
        })

    def forward(self, x, choice, act):
        x = self.choices[choice](x)
        x = self.activations[act](x)
        return x


net = ModuleDict()
fake_img = torch.randn((4, 10, 32, 32))
output = net(fake_img, 'conv', 'relu')
print(net)
# print(output)

输出：

ModuleDict(
  (choices): ModuleDict(
    (conv): Conv2d(10, 10, kernel_size=(3, 3), stride=(1, 1))
    (pool): MaxPool2d(kernel_size=3, stride=3, padding=0, dilation=1, ceil_mode=False)
  )
  (activations): ModuleDict(
    (relu): ReLU()
    (prelu): PReLU(num_parameters=1)
  )
)

容器总结

• nn.Sequential：顺序性，各网络层之间严格按顺序执行，常用于 block 构建。
• nn.ModuleList：迭代性，常用于大量重复网络层构建，通过 for 循环实现重复构建。
• nn.ModuleDict：索引性，常用于可选择的网络层。

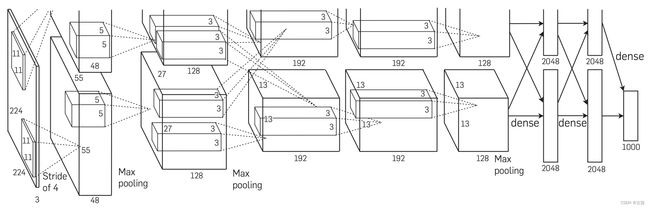
2.2. AlexNet 构建

AlexNet：2012 年以高出第二名 10 多个百分点的准确率获得 ImageNet 分类任务冠军，从此卷积神经网络开始在世界上流行，是划时代的贡献。

AlexNet 特点如下：

• 采用 ReLU：替换饱和激活函数 (例如：Sigmoid)，减轻梯度消失。
• 采用 LRN (Local Response Normalization)：对数据归一化，减轻梯度消失。
• Dropout：提高全连接层的鲁棒性，增加网络的泛化能力。
• Data Augmentation：TenCrop，色彩修改。
• 参考文献：ImageNet Classification with Deep Convolutional Neural Networks

AlexNet 的网络结构可以分为两部分：features 和 classifier。

AlexNet 采用了:

• 卷积、池化、卷积、池化的堆叠方式来提取数据特征，
• 后面再接上三个全连接层进行分类。

这里，我们可以应用 nn.Sequential 中的概念，将前面的卷积池化部分包装成一个 features 模块，将后面的全连接部分包装成一个 classifier 模块，从而将一个复杂网络分解成一个特征提取模块和一个分类模块。

在PyTorch的计算机视觉库torchvision.models中的 AlexNet 的代码中，使用了nn.Sequential来封装网络层。PyTorch 在 torchvision.models 中内置的 AlexNet 实现：

class AlexNet(nn.Module):

    def __init__(self, num_classes=1000):
        super(AlexNet, self).__init__()
        self.features = nn.Sequential(
            nn.Conv2d(3, 64, kernel_size=11, stride=4, padding=2),
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=3, stride=2),
            nn.Conv2d(64, 192, kernel_size=5, padding=2),
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=3, stride=2),
            nn.Conv2d(192, 384, kernel_size=3, padding=1),
            nn.ReLU(inplace=True),
            nn.Conv2d(384, 256, kernel_size=3, padding=1),
            nn.ReLU(inplace=True),
            nn.Conv2d(256, 256, kernel_size=3, padding=1),
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=3, stride=2),
        )
        self.avgpool = nn.AdaptiveAvgPool2d((6, 6))
        self.classifier = nn.Sequential(
            nn.Dropout(),
            nn.Linear(256 * 6 * 6, 4096),
            nn.ReLU(inplace=True),
            nn.Dropout(),
            nn.Linear(4096, 4096),
            nn.ReLU(inplace=True),
            nn.Linear(4096, num_classes),
        )

    def forward(self, x):
        x = self.features(x)
        x = self.avgpool(x)
        x = torch.flatten(x, 1)
        x = self.classifier(x)
        return x

代码示例：

alexnet = torchvision.models.AlexNet()
print(alexnet)

输出：

AlexNet(
  (features): Sequential(
    (0): Conv2d(3, 64, kernel_size=(11, 11), stride=(4, 4), padding=(2, 2))
    (1): ReLU(inplace=True)
    (2): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
    (3): Conv2d(64, 192, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
    (4): ReLU(inplace=True)
    (5): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
    (6): Conv2d(192, 384, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (7): ReLU(inplace=True)
    (8): Conv2d(384, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (9): ReLU(inplace=True)
    (10): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (11): ReLU(inplace=True)
    (12): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
  )
  (avgpool): AdaptiveAvgPool2d(output_size=(6, 6))
  (classifier): Sequential(
    (0): Dropout(p=0.5, inplace=False)
    (1): Linear(in_features=9216, out_features=4096, bias=True)
    (2): ReLU(inplace=True)
    (3): Dropout(p=0.5, inplace=False)
    (4): Linear(in_features=4096, out_features=4096, bias=True)
    (5): ReLU(inplace=True)
    (6): Linear(in_features=4096, out_features=1000, bias=True)
  )
)

---

网络结构分析：

首先，我们将分析每层的数据流维度大小和参数维度大小。给定的输入是一个尺寸为 (1, 3, 512, 512) 的图像张量，其中 1 代表批量大小，3 代表图像通道数（RGB），512x512 代表图像的宽度和高度。

1.第一卷积层（nn.Conv2d(3, 64, kernel_size=11, stride=4, padding=2)）：

• 输入：(1, 3, 512, 512)
• 输出：(1, 64, 128, 128)。输出通道为 64，卷积核大小为 11x11，步长为 4，填充为 2，因此宽度和高度减小了 ((512+4-11)/4)+1=128。
• 参数维度：(64, 3, 11, 11)，其中64个输出通道，3个输入通道，11x11的卷积核。

2.ReLU激活函数：

• 输入：(1, 64, 128, 128)
• 输出：(1, 64, 128, 128)。ReLU 不改变输入的维度。
• 无参数。

3.最大池化层（nn.MaxPool2d(kernel_size=3, stride=2)）：

• 输入：(1, 64, 128, 128)
• 输出：(1, 64, 63, 63)。池化层减小了输入的宽度和高度。((128-3)/2)+1=63。
• 无参数。

4.第二卷积层（nn.Conv2d(64, 192, kernel_size=5, padding=2)）：

• 输入：(1, 64, 63, 63)
• 输出：(1, 192, 63, 63)。输出通道为 192，卷积核大小为 5x5，填充为 2，因此宽度和高度保持不变。
• 参数维度：(192, 64, 5, 5)，其中192个输出通道，64个输入通道，5x5的卷积核。

5.ReLU激活函数：

• 输入：(1, 192, 63, 63)
• 输出：(1, 192, 63, 63)。ReLU 不改变输入的维度。
• 无参数。

6.最大池化层（nn.MaxPool2d(kernel_size=3, stride=2)）：

• 输入：(1, 192, 63, 63)
• 输出：(1, 192, 31, 31)。池化层减小了输入的宽度和高度。((63-3)/2)+1=31。
• 无参数。

7.第三卷积层（nn.Conv2d(192, 384, kernel_size=3, padding=1)）：

• 输入：(1, 192, 31, 31)
• 输出：(1, 384, 31, 31)。输出通道为 384，卷积核大小为 3x3，填充为 1，因此宽度和高度保持不变。
• 参数维度：(384, 192, 3, 3)，其中384个输出通道，192个输入通道，3x3的卷积核。

8.ReLU激活函数：

• 输入：(1, 384, 31, 31)
• 输出：(1, 384, 31, 31)。ReLU 不改变输入的维度。
• 无参数。

9.第四卷积层（nn.Conv2d(384, 256, kernel_size=3, padding=1)）：

• 输入：(1, 384, 31, 31)
• 输出：(1, 256, 31, 31)。输出通道为 256，卷积核大小为 3x3，填充为 1，因此宽度和高度保持不变。
• 参数维度：(256, 384, 3, 3)，其中256个输出通道，384个输入通道，3x3的卷积核。

10.ReLU激活函数：

• 输入：(1, 256, 31, 31)
• 输出：(1, 256, 31, 31)。ReLU 不改变输入的维度。
• 无参数。

11.第五卷积层（nn.Conv2d(256, 256, kernel_size=3, padding=1)）：

• 输入：(1, 256, 31, 31)
• 输出：(1, 256, 31, 31)。输出通道为 256，卷积核大小为 3x3，填充为 1，因此宽度和高度保持不变。
• 参数维度：(256, 256, 3, 3)，其中256个输出通道，256个输入通道，3x3的卷积核。

12.ReLU激活函数：

• 输入：(1, 256, 31, 31)
• 输出：(1, 256, 31, 31)。ReLU 不改变输入的维度。
• 无参数。

13.最大池化层（nn.MaxPool2d(kernel_size=3, stride=2)）：

• 输入：(1, 256, 31, 31)
• 输出：(1, 256, 15, 15)。池化层减小了输入的宽度和高度。((31-3)/2)+1=15。
• 无参数。

14.自适应平均池化层（nn.AdaptiveAvgPool2d((6, 6))）：

• 输入：(1, 256, 15, 15)
• 输出：(1, 256, 6, 6)。这一层将输入张量的宽度和高度调整为目标尺寸（6, 6）。
• 无参数。

15.第一全连接层（nn.Linear(256 * 6 * 6, 4096)）：

• 输入：(1, 256 * 6 * 6)。在传递给全连接层之前，将张量展平。
• 输出：(1, 4096)。
• 参数维度：(4096, 256 * 6 * 6)，其中4096个输出节点，256 * 6 * 6个输入节点。

16.ReLU激活函数：

• 输入：(1, 4096)
• 输出：(1, 4096)。ReLU 不改变输入的维度。
• 无参数。

17.第二全连接层（nn.Linear(4096, 4096)）：

• 输入：(1, 4096)
• 输出：(1, 4096)。
• 参数维度：(4096, 4096)，其中4096个输出节点，4096个输入节点。

18.ReLU激活函数：

• 输入：(1, 4096)
• 输出：(1, 4096)。ReLU 不改变输入的维度。
• 无参数。

19.第三全连接层（nn.Linear(4096, num_classes)）：

• 输入：(1, 4096)
• 输出：(1, num_classes)。在这个例子中，num_classes 默认为 1000，因此输出维度为 (1, 1000)。
• 参数维度：(1000, 4096)，其中1000个输出节点，4096个输入节点。

现在，我们来计算总共需要学习的参数个数：

• 第一卷积层：64 * 3 * 11 * 11 = 23,296
• 第二卷积层：192 * 64 * 5 * 5 = 307,200
• 第三卷积层：384 * 192 * 3 * 3 = 663,552
• 第四卷积层：256 * 384 * 3 * 3 = 884,736
• 第五卷积层：256 * 256 * 3 * 3 = 589,824
• 第一全连接层：4096 * 256 * 6 * 6 = 37,748,736
• 第二全连接层：4096 * 4096 = 16,777,216
• 第三全连接层：1000 * 4096 = 4,096,000

将所有参数加起来，我们得到：23,296 + 307,200 + 663,552 + 884,736 + 589,824 + 37,748,736 + 16,777,216 + 4,096,000 = 60,990,560。

所以，整个 AlexNet 网络总共需要学习 60,990,560 个参数。

Dropout 层（Dropout(p=0.5, inplace=False)）并不会改变参数的大小。Dropout 是一种正则化技术，它在训练过程中随机地将部分神经元的输出设置为零，以防止过拟合。在测试和推理阶段，Dropout 层不会对输入数据产生任何影响。Dropout 层没有学习参数，因此不会对需要学习的参数个数产生影响。

2.3. 总结

本节中，我们学习了 3 种不同的模型容器：Sequential、ModuleList、ModuleDict，以及 AlexNet 的搭建。下节课中，我们将学习 nn 中网络层的具体使用。

3.nn 网络层：卷积层

在上节课中，我们学习了如何在 PyTorch 中搭建神经网络模型，以及在搭建网络的过程中常用的容器： Sequential、ModuleList 和 ModuleDict。本节课开始，我们将学习 PyTorch 中常见的网络层，现在我们先重点学习卷积层。

3.1. 1d/2d/3d卷积

卷积运算 (Convolution)：卷积核在输入信号 (图像) 上滑动，相应位置上进行 乘加。 卷积核 (Kernel)：又称为滤波器/过滤器，可认为是某种模式/某种特征。

卷积过程类似于用一个模版去图像上寻找与它相似的区域，与卷积核模式越相似，激活值越高，从而实现特征提取。所以在深度学习中，我们可以将卷积核视为特征提取器。

下图是 AlexNet 卷积核的可视化，我们发现卷积核实际上学习到的是 边缘、条纹、色彩 这些细节模式：

这进一步验证了卷积核是图像的某种特征提取器，而具体的特征模式则完全由模型学习得到。

卷积维度 (Dimension)：一般情况下,一个卷积核在一个信号上沿几个维度上滑动，就是几维卷积。

3.1.1.1d 卷积

3.1.2.2d 卷积

3.1.3.3d 卷积

可以看到，一个卷积核在一个信号上沿几个维度滑动，就是几维卷积。注意这里我们强调 一个卷积核 和 一个信号，因为通常我们会涉及包含多个卷积核和多个信号的卷积操作，这种情况下怎么去判断卷积的维度呢，这里我们可以先思考一下。

3.2. 卷积-nn.Conv2d()

nn.Conv2d
功能：对多个二维平面信号进行二维卷积。

nn.Conv2d(
    in_channels,
    out_channels,
    kernel_size,
    stride=1,
    padding=0,
    dilation=1,
    groups=1,
    bias=True,
    padding_mode='zeros'
)

主要参数：

• in_channels：输入通道数。
• out_channels：输出通道数，等价于卷积核个数。
• kernel_size：卷积核尺寸。
• stride：步长。下面是一个步长为 2 的卷积：

• padding：填充个数。常用于保持输入输出图像尺寸匹配，可以用于提高输出图像的分辨率：

• dilation：空洞卷积大小。常用于图像分割任务，目的是提高感受野，即输出图像的一个像素对应输入图像上更大的一块区域：

• groups：分组卷积的组数。常用于模型的轻量化。例如，Alexnet 当时由于硬件限制采用了两组卷积操作：

• bias：偏置。最终输出响应值时需加上偏置项。

卷积尺寸计算：

代码示例，这里使用 inputchannel 为 3，output_channel 为 1 ，卷积核大小为 3×3
的卷积核nn.Conv2d(3, 1, 3)，使用nn.init.xavier_normal()方法初始化网络的权值。代码如下：

import os
import torch.nn as nn
from PIL import Image
from torchvision import transforms
from matplotlib import pyplot as plt
from tools.common_tools import transform_invert, set_seed

set_seed(3)  # 设置随机种子，用于调整卷积核权值的状态。

# ================================= load img ==================================
path_img = os.path.join(os.path.dirname(os.path.abspath(__file__)), "lena.png")
img = Image.open(path_img).convert('RGB')  # 0~255

# convert to tensor
img_transform = transforms.Compose([transforms.ToTensor()])
img_tensor = img_transform(img)
img_tensor.unsqueeze_(dim=0)    # C*H*W to B*C*H*W

# ========================= create convolution layer ==========================
conv_layer = nn.Conv2d(3, 1, 3)   # input:(i, o, size) weights:(o, i , h, w)
nn.init.xavier_normal_(conv_layer.weight.data)

# calculation
img_conv = conv_layer(img_tensor)

# =========================== visualization ==================================
print("卷积前尺寸:{}\n卷积后尺寸:{}".format(img_tensor.shape, img_conv.shape))
img_conv = transform_invert(img_conv[0, 0:1, ...], img_transform)
img_raw = transform_invert(img_tensor.squeeze(), img_transform)
plt.subplot(122).imshow(img_conv, cmap='gray')
plt.subplot(121).imshow(img_raw)
plt.show()

输出结果：

卷积前尺寸:torch.Size([1, 3, 512, 512])
卷积后尺寸:torch.Size([1, 1, 510, 510])

• set.seed(1) 时的输出：

• set.seed(2) 时的输出：

• set.seed(3) 时的输出：

可以看到，不同的卷积核权值对应的输出是不相同的。通常，我们会在卷积层中设置多个卷积核，以提取不同的特征。

在上面的例子中，我们使用一个 3 维的卷积核实现了一个 2d 卷积：

我们的输入是一个 RGB 的二维图像，它包含 3 个色彩通道。然后，我们将创建 3 个二维卷积核，不同通道对应不同的卷积核。我们将三个通道的卷积结果相加，然后再加上偏置项，得到最终的卷积结果。

3.3. 转置卷积-nn.ConvTranspose

转置卷积 (Transpose Convolution) 又称为 反卷积 (Deconvolution) 注 1 或者 部分跨越卷积 (Fractionally strided Convolution)，常见于图像分割任务中，主要用于对图像进行 上采样 (UpSample)。

(注 1：这里我们说的反卷积不同于信号系统中的反卷积)。

为什么称为转置卷积？

正常卷积：

假设图像尺寸为 $4\times 4$, 卷积核为 $3\times 3$, padding $=0$, stride $=1$ 。

• 图像: $I_{16\times 1}$, 这里 16 是输入图像的像素总数, 1 表示图片张数。
  。 卷积核： $K_{4\times 16}$, 这里 4 是输出图像的像素总数, 16 是由卷积核中的 9 个元素另外补零 后得到。
• 输出: $O_{4\times 1}=K_{1\times 16}\times I_{16\times 1}$

---

• 转置卷积: 上采样，输出图像比输入图像尺寸更大。

假设图像尺寸为 $2\times 2$, 卷积核为 $3\times 3$, padding $=0$, stride $=1$ 。

• 图像: $I_{4\times 1}$, 这里 4 是输入图像的像素总数, 1 表示图片张数。
  。 卷积核: $K_{16\times 4}$, 这里 16 是输出图像的像素总数, 4 是由卷积核中的 9 个元素剔除一部 分后得到。
  。输出: $O_{16\times 1}=K_{16\times 4}\times I_{4\times 1}$

可以看到，转置卷积与正常卷积的卷积核尺寸在形状上是转置关系，这也是我们将其称为转置卷积的原因。注意，二者只是在形状上是转置关系，但它们的权值是完全不同的。也就是说，该卷积过程是不可逆的，即卷积后再转置卷积，得到的图像和初始图像是完全不同的。

• nn.ConvTranspose2d

功能：转置卷积实现上采样。

nn.ConvTranspose2d(
    in_channels,
    out_channels,
    kernel_size,
    stride=1,
    padding=0,
    output_padding=0,
    groups=1,
    bias=True,
    dilation=1,
    padding_mode='zeros'
)

主要参数：

• in_channels：输入通道数。
• out_channels：输出通道数。
• kernel_size：卷积核尺寸。
• stride：步长。
• padding：填充个数。
• dilation：空洞卷积大小。
• groups：分组卷积设置。
• bias：偏置。

尺寸计算：

• 简化版 (不带 padding 和 dilation)：

$${\mathrm{out}}_{\text{size}}=({\mathrm{in}}_{\text{size}}-1)\times \mathrm{stride}+{\mathrm{kernel}}_{\text{size}}$$

• 完整版：

$$H_{\text{out}}=(H_{\text{in}}-1)\times \mathrm{stride}[0]-$$$$2\times \mathrm{padding}[0]+\mathrm{dilation}[0]\times (\text{kernelsize}[0]-1)+output\_padding[0]+1$$
代码示例：

import os
import torch.nn as nn
from PIL import Image
from torchvision import transforms
from matplotlib import pyplot as plt
from tools.common_tools import transform_invert, set_seed

set_seed(3)  # 设置随机种子，用于调整卷积核权值的状态。

# ================================= load img ==================================
path_img = os.path.join(os.path.dirname(os.path.abspath(__file__)), "lena.png")
img = Image.open(path_img).convert('RGB')  # 0~255

# convert to tensor
img_transform = transforms.Compose([transforms.ToTensor()])
img_tensor = img_transform(img)
img_tensor.unsqueeze_(dim=0)    # C*H*W to B*C*H*W

# ========================= create convolution layer ==========================
conv_layer = nn.ConvTranspose2d(3, 1, 3, stride=2)   # input:(i, o, size)
nn.init.xavier_normal_(conv_layer.weight.data)

# calculation
img_conv = conv_layer(img_tensor)

# =========================== visualization ==================================
print("卷积前尺寸:{}\n卷积后尺寸:{}".format(img_tensor.shape, img_conv.shape))
img_conv = transform_invert(img_conv[0, 0:1, ...], img_transform)
img_raw = transform_invert(img_tensor.squeeze(), img_transform)
plt.subplot(122).imshow(img_conv, cmap='gray')
plt.subplot(121).imshow(img_raw)
plt.show()

输出结果：

卷积前尺寸:torch.Size([1, 3, 512, 512])
卷积后尺寸:torch.Size([1, 1, 1025, 1025])

可以看到，在经过转置卷积上采样后，图像出现了一个奇怪的现象：输出的图像上有许多网格。这被称为 棋盘效应 (Checkerboard Artifacts)，是由于转置卷积中的不均匀重叠造成的。关于棋盘效应的解释以及解决方法请参考论文 Deconvolution and Checkerboard Artifacts。

3.4. 总结

本节中，我们学习了 nn 模块中卷积层。在下次课程中，我们将学习 nn 模块中的其他常用网络层。

4.nn 网络层：池化层、全连接层和激活函数层

上节中，我们学习了网络层中的卷积层。本节中，我们将继续学习其他几种网络层：池化层、线性层和激活函数层。

4.1. 池化层-Pooling Layer

池化的作用则体现在降采样：

• 保留显著特征、降低特征维度，增大 kernel 的感受野。
• 另外一点值得注意：pooling 也可以提供一些旋转不变性。

池化层可对提取到的特征信息进行降维，一方面使特征图变小，简化网络计算复杂度并在一定程度上避免过拟合的出现；一方面进行特征压缩，提取主要特征。

有最大池化和平均池化两张方式。

池化运算 (Pooling)：对信号进行 收集 并 总结，类似水池收集水资源，因而得名池化层。

• “收集”：多变少。
• “总结”：最大值/平均值。

最大池化 vs. 平均池化：

4.1.1.nn.MaxPool2d

功能：对二维信号（图像）进行最大值池化。

nn.MaxPool2d(
    kernel_size,
    stride=None,
    padding=0,
    dilation=1,
    return_indices=False,
    ceil_mode=False
)

主要参数：

• kernel_size：池化核尺寸。
• stride：步长。步长，通常与 kernel_size 一致
• padding：填充个数。填充宽度，主要是为了调整输出的特征图大小，一般把 padding 设置合适的值后，保持输入和输出的图像尺寸不变。
• dilation：池化核间隔大小。池化间隔大小，默认为 1。常用于图像分割任务中，主要是为了提升感受野
• ceil_mode：尺寸是否向上取整。用于计算输出特征图尺寸，默认设置为向下取整。默认为 False，尺寸向下取整。为 True 时，尺寸向上取整
• return_indices：记录池化像素索引。通常在最大值反池化上采样时使用。为 True 时，返回最大池化所使用的像素的索引，这些记录的索引通常在反最大池化时使用，把小的特征图反池化到大的特征图时，每一个像素放在哪个位置。

下图 (a) 表示反池化，(b) 表示上采样，(c) 表示反卷积。

代码示例：

import os
import torch
import torch.nn as nn
from torchvision import transforms
from matplotlib import pyplot as plt
from PIL import Image
from tools.common_tools import transform_invert, set_seed

set_seed(1)  # 设置随机种子

# ================================= load img ==================================
path_img = os.path.join(os.path.dirname(os.path.abspath(__file__)), "lena.png")
img = Image.open(path_img).convert('RGB')  # 0~255

# convert to tensor
img_transform = transforms.Compose([transforms.ToTensor()])
img_tensor = img_transform(img)
img_tensor.unsqueeze_(dim=0)    # C*H*W to B*C*H*W

# ========================== create maxpool layer =============================
maxpool_layer = nn.MaxPool2d((2, 2), stride=(2, 2))   # input:(i, o, size) weights:(o, i , h, w)
img_pool = maxpool_layer(img_tensor)

# ================================= visualization =============================
print("池化前尺寸:{}\n池化后尺寸:{}".format(img_tensor.shape, img_pool.shape))
img_pool = transform_invert(img_pool[0, 0:3, ...], img_transform)
img_raw = transform_invert(img_tensor.squeeze(), img_transform)
plt.subplot(122).imshow(img_pool)
plt.subplot(121).imshow(img_raw)
plt.show()

输出结果：

池化前尺寸:torch.Size([1, 3, 512, 512])
池化后尺寸:torch.Size([1, 3, 256, 256])

可以看到，经过最大池化后的图像尺寸减小了一半，而图像质量并没有明显降低。因此，池化操作可以剔除图像中的冗余信息，以及减小后续的计算量。

4.1.2.nn.AvgPool2d

功能：对二维信号（图像）进行平均值池化。

nn.AvgPool2d(
    kernel_size,
    stride=None,
    padding=0,
    ceil_mode=False,
    count_include_pad=True,
    divisor_override=None
)

主要参数：

• kernel_size：池化核尺寸。

• stride：步长。通常与 kernel_size 一致

• padding：填充个数。填充宽度，主要是为了调整输出的特征图大小，一般把 padding 设置合适的值后，保持输入和输出的图像尺寸不变。

• dilation：池化间隔大小，默认为 1。常用于图像分割任务中，主要是为了提升感受野

• ceil_mode：尺寸向上取整。默认为 False，尺寸向下取整。为 True 时，尺寸向上取整

• count_include_pad：是否将填充值用于平均值的计算。在计算平均值时，是否把填充值考虑在内计算

• divisor_override：除法因子。计算平均值时代替像素个数作为分母。除法因子。在计算平均值时，分子是像素值的总和，分母默认是像素值的个数。如果设置了 divisor_override，把分母改为 divisor_override。

代码示例：

import os
import torch
import torch.nn as nn
from torchvision import transforms
from matplotlib import pyplot as plt
from PIL import Image
from tools.common_tools import transform_invert, set_seed

set_seed(1)  # 设置随机种子

# ================================= load img ==================================
path_img = os.path.join(os.path.dirname(os.path.abspath(__file__)), "lena.png")
img = Image.open(path_img).convert('RGB')  # 0~255

# convert to tensor
img_transform = transforms.Compose([transforms.ToTensor()])
img_tensor = img_transform(img)
img_tensor.unsqueeze_(dim=0)    # C*H*W to B*C*H*W

# ========================== create avgpool layer =============================
avgpoollayer = nn.AvgPool2d((2, 2), stride=(2, 2))   # input:(i, o, size) weights:(o, i , h, w)
img_pool = avgpoollayer(img_tensor)

# =============================== visualization ===============================
print("池化前尺寸:{}\n池化后尺寸:{}".format(img_tensor.shape, img_pool.shape))
img_pool = transform_invert(img_pool[0, 0:3, ...], img_transform)
img_raw = transform_invert(img_tensor.squeeze(), img_transform)
plt.subplot(122).imshow(img_pool)
plt.subplot(121).imshow(img_raw)
plt.show()

输出结果：

池化前尺寸:torch.Size([1, 3, 512, 512])
池化后尺寸:torch.Size([1, 3, 256, 256])

同样，图像尺寸减小了一半，而质量并没有明显降低。另外，如果我们仔细对比最大池化与平均池化的结果，可以发现最大池化后的图像会偏亮一些，而平均池化后的图像会偏暗一些，这是由于两种池化操作采用不同的计算方式造成的 (像素值越大，图像亮度越高)。

4.1.3.divisor_override 的使用

现在，我们来看一下除法因子的使用。这里，我们初始化一个
的图像，并且采用一个
的窗口，步长设置为
。

正常的平均池化：

img_tensor = torch.ones((1, 1, 4, 4))
avgpool_layer = nn.AvgPool2d((2, 2), stride=(2, 2))
img_pool = avgpool_layer(img_tensor)

print("raw_img:\n{}\npooling_img:\n{}".format(img_tensor, img_pool))

输出结果：

raw_img:
tensor([[[[1., 1., 1., 1.],
          [1., 1., 1., 1.],
          [1., 1., 1., 1.],
          [1., 1., 1., 1.]]]])
pooling_img:
tensor([[[[1., 1.],
          [1., 1.]]]])

计算池化后的像素值：

$$\frac{1+1+1+1}{4}=1$$

divisor_override=3 的平均池化：

img_tensor = torch.ones((1, 1, 4, 4))
avgpool_layer = nn.AvgPool2d((2, 2), stride=(2, 2), divisor_override=3)
img_pool = avgpool_layer(img_tensor)

print("raw_img:\n{}\npooling_img:\n{}".format(img_tensor, img_pool))

输出结果：

raw_img:
tensor([[[[1., 1., 1., 1.],
          [1., 1., 1., 1.],
          [1., 1., 1., 1.],
          [1., 1., 1., 1.]]]])
pooling_img:
tensor([[[[1.3333, 1.3333],
          [1.3333, 1.3333]]]])

计算池化后的像素值：

$$\frac{1+1+1+1}{3}=1.3333$$

目前为止，我们学习了最大池化和平均池化，它们都是对图像实现下采样的过程，即输入尺寸较大的图像，输出尺寸较小的图像。下面我们将学习反池化，即将小尺寸图像变为大尺寸图像。

4.1.4.nn.MaxUnpool2d

功能：对二维信号（图像）进行最大值反池化上采样。

nn.MaxUnpool2d(
    kernel_size,
    stride=None,
    padding=0
)

forward(self, input, indices, output_size=None)

主要参数：

• kernel_size：池化核尺寸。
• stride：步长。步长，通常与 kernel_size 一致
• padding：填充个数。

最大值反池化：

早期的自编码器和图像分割任务中都会涉及一个上采样的操作, 当时普遍采用的方法是最大值反池化 上采样。上图左半部分是最大池化过程, 原始 $4\times 4$ 的图像经过最大池化后得到一个 $2\times 2$ 的下采 样图像, 然后经过一系列的网络层之后, 进入上图右半部分的上采样解码器, 即将一个尺寸较小的图 像经过上采样得到一个尺寸较大的图像。此时, 涉及到的一个问题是: 我们应该将像素值放到什么位 置。例如：右边 $2\times 2$ 图像中的左上角的 3 应当放入最终 $4\times 4$ 图像中的左上部分的 4 个像素中的 哪一个? 这时, 我们就可以利用之前最大池化过程中记录的池化像素索引, 将 3 放入之前原始 $4\times 4$ 图像中左上角的 4 个像素中最大值对应的位置。

代码示例：

# pooling
img_tensor = torch.randint(high=5, size=(1, 1, 4, 4), dtype=torch.float)
maxpool_layer = nn.MaxPool2d((2, 2), stride=(2, 2), return_indices=True)
img_pool, indices = maxpool_layer(img_tensor)

# unpooling
img_reconstruct = torch.randn_like(img_pool, dtype=torch.float)
maxunpool_layer = nn.MaxUnpool2d((2, 2), stride=(2, 2))
img_unpool = maxunpool_layer(img_reconstruct, indices)

print("raw_img:\n{}\nimg_pool:\n{}".format(img_tensor, img_pool))
print("img_reconstruct:\n{}\nimg_unpool:\n{}".format(img_reconstruct, img_unpool))

输出结果：

raw_img:
tensor([[[[0., 4., 4., 3.],
          [3., 3., 1., 1.],
          [4., 2., 3., 4.],
          [1., 3., 3., 0.]]]])
img_pool:
tensor([[[[4., 4.],
          [4., 4.]]]])
img_reconstruct:
tensor([[[[-1.0276, -0.5631],
          [-0.8923, -0.0583]]]])
img_unpool:
tensor([[[[ 0.0000, -1.0276, -0.5631,  0.0000],
          [ 0.0000,  0.0000,  0.0000,  0.0000],
          [-0.8923,  0.0000,  0.0000, -0.0583],
          [ 0.0000,  0.0000,  0.0000,  0.0000]]]])

这里, 我们初始化一个 $4\times 4$ 的图像, 并且采用一个 $2\times 2$ 的窗口, 步长设置为 2 。首先, 我们对 其进行最大值池化, 并记录其中的最大值像素的索引。然后, 我们进行反池化, 这里反池化的输入和 之前最大池化后得到的图像尺寸是一样的, 并且反池化层的窗口和步长与之前最大池化层是一致的。 最后，我们将输入和索引传入反池化层，得到与原始图像尺寸相同的图像。

4.2. 线性层-Linear Layer

线性层 (Linear Layer) 又称 全连接层 (Full-connected Layer)，其每个神经元与上一层所有神经元相连，实现对前一层的 线性组合/线性变换。

在卷积神经网络进行分类的时候，在输出之前，我们通常会采用一个全连接层对特征进行处理，在 PyTorch 中，全连接层又称为线性层，因为如果不考虑激活函数的非线性性质，那么全连接层就是对输入数据进行一个线性组合。

每个神经元都和前一层中的所有神经元相连，每个神经元的计算方式是对上一层的加权求和的过程。因此，线性层可以采用矩阵乘法来实现。注意，上图中我们暂时忽略了偏置项。

nn.Linear
功能：对一维信号（向量）进行线性组合。

nn.Linear(in_features, out_features, bias=True)

主要参数：

• in_features：输入结点数。
• out_features：输出结点数。
• bias：是否需要偏置。

计算公式：

$$y=x{W}^T+b$$

代码示例：

inputs = torch.tensor([[1., 2, 3]])
linear_layer = nn.Linear(3, 4)
linear_layer.weight.data = torch.tensor([[1., 1., 1.],
                                         [2., 2., 2.],
                                         [3., 3., 3.],
                                         [4., 4., 4.]])
linear_layer.bias.data.fill_(0.5)
output = linear_layer(inputs)

print(inputs, inputs.shape)
print(linear_layer.weight.data, linear_layer.weight.data.shape)
print(output, output.shape)

输出结果：

tensor([[1., 2., 3.]]) torch.Size([1, 3])
tensor([[1., 1., 1.],
        [2., 2., 2.],
        [3., 3., 3.],
        [4., 4., 4.]]) torch.Size([4, 3])
tensor([[ 6.5000, 12.5000, 18.5000, 24.5000]], grad_fn=) torch.Size([1, 4])

4.3. 激活函数层-Activation Layer

激活函数 (Activation Function) 是对特征进行非线性变换，赋予多层神经网络具有 深度 的意义。

如果没有非线性变换，由于矩阵乘法的结合性，多个线性层的组合等价于一个线性层:

在上面最后一步中，由于矩阵乘法的结合性，我们可以把右边三个权重矩阵先结合相乘，可以得到一个大的权重矩阵 W 。这样我们可以看到，我们的 output 实际上就是输入 X 乘以一个大的权重矩阵 W 。

因此，这里的三层线性全连接层实际上等价于一个一层的全连接层，这是由于线性运算当中矩阵乘法的结合性导致的，并且这里我们没有引入非线性激活函数。如果加上 非线性激活函数，这一结论将不再成立，因此我们说，激活函数赋予了多层神经网络具有 深度 的意义。

4.3.1.nn.Sigmoid

计算公式:
$$y=\frac{1}{1+e^{-x}}$$
梯度公式:
$$y^{\prime }=y\ast (1-y)$$
特性:

• 输出值在 $(0,1)$, 符合概率性质。
• 导数范围是 $[0,0.25]$, 容易导致梯度消失。
• 输出为非 0 均值, 会破坏数据分布。

4.3.2.nn.tanh

计算公式:
$$y=\frac{\sin x}{\cos x}=\frac{e^x-e^{-x}}{e^x+e^{-x}}=\frac{2}{1+e^{-2x}}+1$$
梯度公式：
$$y^{\prime }=1-y^2$$
特性:

• 输出值在 $(-1,1)$, 数据符合 0 均值。
• 导数范围是 $(0,1)$, 容易导致梯度消失。

4.3.3.nn.ReLU

计算公式:
$$y=\max (0,x)$$
梯度公式：
$$y^{\prime }=\{\begin{array}{ll}1,& x>0\\ \text{ undefined, },& x=0\\ 0,& x<0\end{array}$$
特性:

• 输出值均为正数, 负半轴导致死神经元。
• 导数是 1 , 可以缓解梯度消失, 但容易引发梯度爆炸。

针对 ReLU 激活函数负半轴死神经元的问题，有以下几种改进方式：

• nn.LeakyReLU

  • negative_slope：负半轴斜率。蓝色曲线，斜率很小。

• nn.PReLU

  • init：可学习斜率。

• nn.RReLU

  • lower：均匀分布下限。
  • upper：均匀分布上限。

4.4. 总结

本节中，我们学习了 nn 模块中池化层、线性层和激活函数层。在池化层中有正常的最大值池化、均值池化，还有图像分割任务中常用的反池化 —— MaxUnpool；在激活函数中我们学习了 Sigmoid、Tanh 和 Relu，以及 Relu 的各种变体，如 LeakyReLU、PReLU、RReLU。下节中，我们将学习网络层权值的初始化。