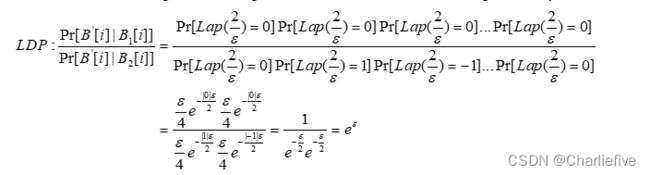Locally Differentially Private Protocols for Frequency Estimation论文笔记
文章目录
- 1.Pure LDP Protocol
-
- 1.1相关背景
- 1.2支持集
- 1.3相关定义
- 2.Basic one-time RAPPOR
- 3.Rappor
- 4.Direct Encoding
-
- 4.1GRR
- 4.2RR
- 5.Unary Encoding
-
- 5.1Symmetric Unary Encoding
- 5.1Optimized Unary Encoding
- 6.Local Hashing
-
- 6.1Binary Local Hashing
- 6.2Local Hashing
- 6.3Optimal Local Hashing
- 7.Histogram Encoding
-
- 7.1Summation with Histogram Encoding不纯
- 7.2Thresholding with Histogram Encoding
本文重点:搞清楚真实值、观察值、估计值之间的关系。
1.Pure LDP Protocol
1.1相关背景
基于LDP频率估计的几种方法,如何比较它们?在同一隐私水平下,哪个协议能提供更好的精度和更低的通信代价?
为了回答这些问题,本文定义了一个Pure LDP Protocols
- Pure LDP Protocols是一种简单的、通用的协议
- 给出了估计方差的公式,统一标准,目前大多数现有的方法都能适应这个协议
- 该协议还能够精确地分析和比较不同方法的准确性,并对它们进行归纳和优化
1.2支持集
Pr [ PE ( v 1 ) ∈ { y ∣ v 1 ∈ Support ( y ) } ] = p ∗ , ∀ v 2 ≠ v 1 Pr [ PE ( v 2 ) ∈ { y ∣ v 1 ∈ Support ( y ) } ] = q ∗ . \text{Pr}\left[\text{PE}(v_1)\in\{y\mid v_1\in\text{Support}(y)\}\right]=p^*,\\ \forall_{v_2\neq v_1}\text{Pr}\left[\text{PE}(v_2)\in\{y\mid v_1\in\text{Support}(y)\}\right]=q^*. Pr[PE(v1)∈{y∣v1∈Support(y)}]=p∗,∀v2=v1Pr[PE(v2)∈{y∣v1∈Support(y)}]=q∗.

以这个例子为例(个人理解):当i等于3时,满足编码后B0的向量中第3个位置为1的集合,再通过集合映射到原来的用户,用户所组成的集合,即为支持集。
定义了Support函数:它将每个可能的输出y映射到y支持的一组输入值。
example:Basic RAPPOR 输出的二进制变量值B被解释为支持每个对应位为1的输入 Support(B)={i|B[i]=1} d=5,i=2,Encode(i)=[0,1,0,0,0] Support(B[2])=x表示的是有哪些x值经过编码以后第2个位置为1,满足条件的集合。
1.3相关定义
条件:
- pure LDP协议要求任何值v映射到其所支持集的概率是相等的(每个p或者q都是独立且相等)
- p* > q*
步骤说明:
S u p p o r t ( B ) = { i ∣ B [ i ] = 1 } Support(B) = \{ i|B[i] = 1\} Support(B)={i∣B[i]=1}
S u p p o r t ( y 1 ) = { i ∣ y 1 [ i ] = 1 } = { v 1 , v 4 } Support({y_1}) = \{ i|{y_1}[i] = 1\} {\text{ = \{ }}{v_1}{\text{,}}{{\text{v}}_4}{\text{\} }} Support(y1)={i∣y1[i]=1} = { v1,v4}
令 { y 1 ∣ { v 1 , v 4 } ∈ S u p p o r t ( y 1 ) } = t 令\{ {y_1}|\{ {v_1},{v_4}\} \in Support({y_1})\} = t 令{y1∣{v1,v4}∈Support(y1)}=t
可以得出
Pr [ P E ( v 1 ) ∈ t ] = Pr [ P E ( v 4 ) ∈ t ] = p ∗ \Pr [PE({v_1}) \in t] = \Pr [PE({v_4}) \in t] = {p^*} Pr[PE(v1)∈t]=Pr[PE(v4)∈t]=p∗ ∀ v j ≠ v 1 Pr [ P E ( v j ) ∈ t ] = q ∗ {\forall _{{v_j} \ne {v_1}}}\Pr [PE({v_j}) \in t] = {q^*} ∀vj=v1Pr[PE(vj)∈t]=q∗
2.Basic one-time RAPPOR
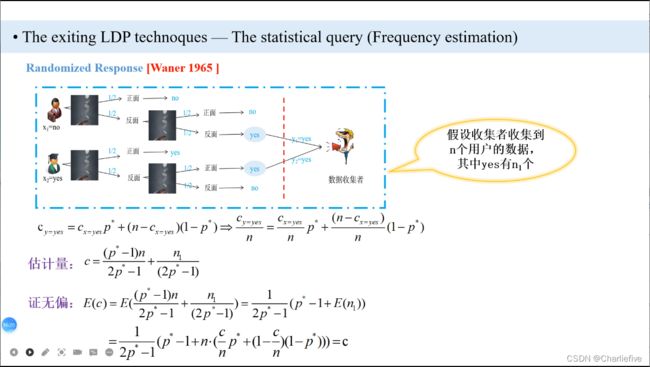
举一个满足PureLDP的例子Basic one-time RAPPOR:

参考图见上图
p*满足相等(真实扰动概率):
p ∗ [ y 1 ∣ P E ( v 1 ) ] = p ∗ [ y 1 ∣ P E ( v 4 ) ] = ( 1 − 1 2 f ) 4 {p^*}[{y_1}|PE({v_1})] = {p^*}[{y_1}|PE({v_4})] = {(1 - \frac{1}{2}f)^4} p∗[y1∣PE(v1)]=p∗[y1∣PE(v4)]=(1−21f)4
q*满足相等(非真实扰动概率):
∀ v j ≠ v i , q ∗ [ y 1 ∣ P E ( v 2 ) ] = ( 1 − 1 2 f ) ( 1 2 f ) 2 ( 1 − 1 2 f ) = ( 1 − 1 2 f ) 2 ( 1 2 f ) 2 {\forall _{{v_j} \ne {v_i}}},{q^*}[{y_1}|PE({v_2})] = (1 - \frac{1}{2}f){(\frac{1}{2}f)^2}(1 - \frac{1}{2}f) = {(1 - \frac{1}{2}f)^2}{(\frac{1}{2}f)^2} ∀vj=vi,q∗[y1∣PE(v2)]=(1−21f)(21f)2(1−21f)=(1−21f)2(21f)2
q ∗ [ y 1 ∣ P E ( v 3 ) ] → = ( 1 2 f ) ( 1 2 f ) ( 1 − 1 2 f ) 2 = ( 1 − 1 2 f ) 2 ( 1 2 f ) 2 {q^*}[{y_1}|PE({v_3})] \to = (\frac{1}{2}f)(\frac{1}{2}f){(1 - \frac{1}{2}f)^2} = {(1 - \frac{1}{2}f)^2}{(\frac{1}{2}f)^2} q∗[y1∣PE(v3)]→=(21f)(21f)(1−21f)2=(1−21f)2(21f)2
Aggregation:
概率表达式:
P ( y = 1 ) = π p ∗ + ( 1 − π ) q ∗ P ( y = 0 ) = π q ∗ + ( 1 − π ) p ∗ P(y = 1) = \pi p* + (1 - \pi )q*P(y = 0) = \pi q* + (1 - \pi )p* P(y=1)=πp∗+(1−π)q∗P(y=0)=πq∗+(1−π)p∗
构建似然函数:
L = [ π p ∗ + ( 1 − π ) q ∗ ] n 1 [ π q ∗ + ( 1 − π ) p ∗ ] n − n 1 L = {[\pi p* + (1 - \pi )q*]^{{n_1}}}{[\pi q* + (1 - \pi )p*]^{n - {n_1}}} L=[πp∗+(1−π)q∗]n1[πq∗+(1−π)p∗]n−n1
l n L = n 1 l n [ π p ∗ + ( 1 − π ) q ∗ ] + ( n − n 1 ) l n [ π q ∗ + ( 1 − π ) p ∗ ] lnL = {n_1}ln[\pi p* + (1 - \pi )q*] + (n - {n_1})ln[\pi q* + (1 - \pi )p*] lnL=n1ln[πp∗+(1−π)q∗]+(n−n1)ln[πq∗+(1−π)p∗]
求偏导:
∂ l n L ∂ π = n 1 ( p ∗ − q ∗ ) π p ∗ + ( 1 − π ) q ∗ + ( n − n 1 ) ( q ∗ − p ∗ ) π q ∗ + ( 1 − π ) p ∗ = 0 \frac{{\partial lnL}}{{\partial \pi }} = \frac{{{n_1}(p* - q*)}}{{\pi p* + (1 - \pi )q*}} + \frac{{(n - {n_1})(q* - p*)}}{{\pi q* + (1 - \pi )p*}} = 0 ∂π∂lnL=πp∗+(1−π)q∗n1(p∗−q∗)+πq∗+(1−π)p∗(n−n1)(q∗−p∗)=0
估计量:
π ^ = n 1 / n − q ∗ p ∗ − q ∗ ⇒ c ^ = n 1 − n ∗ q p ∗ − q ∗ \hat \pi = \frac{{{n_1}/n - q*}}{{p* - q*}} \Rightarrow \hat c = \frac{{{n_1} - n*q}}{{p* - q*}} π^=p∗−q∗n1/n−q∗⇒c^=p∗−q∗n1−n∗q

无偏性证明:
对于 P u r e P r o t o c o l s , c ~ = n 1 − q ∗ n p ∗ − q ∗ Pure\;Protocols,\tilde c = \frac{{{n_1} - q*n}}{{p* - q*}} PureProtocols,c~=p∗−q∗n1−q∗n是无偏的
E ( c ~ ) = E ( n 1 − q ∗ n p ∗ − q ∗ ) = E ( n 1 ) − q ∗ n p ∗ − q ∗ = n ( π p ∗ + ( 1 − π ) q ∗ ) − q ∗ n p ∗ − q ∗ = n π p ∗ + q ∗ − π q ∗ − q ∗ p ∗ − q ∗ = π n E(\tilde c) = E(\frac{{{n_1} - q*n}}{{p* - q*}}) = \frac{{E({n_1}) - q*n}}{{p* - q*}} = \frac{{n(\pi p* + (1 - \pi )q*) - q*n}}{{p* - q*}} = n\frac{{\pi p* + q* - \pi q* - q*}}{{p* - q*}} = \pi n E(c~)=E(p∗−q∗n1−q∗n)=p∗−q∗E(n1)−q∗n=p∗−q∗n(πp∗+(1−π)q∗)−q∗n=np∗−q∗πp∗+q∗−πq∗−q∗=πn
方差:
V a r ( c ~ ) = V a r ( n 1 − q ∗ n p ∗ − q ∗ ) = V a r ( n 1 ) ( p ∗ − q ∗ ) 2 = n π p ∗ ( 1 − p ∗ ) + n ( 1 − π ) q ∗ ( 1 − q ∗ ) ( p ∗ − q ∗ ) 2 = n π p ∗ − n π p ∗ 2 + n q ∗ ( 1 − q ∗ ) − n π q ∗ + n π q ∗ 2 ( p ∗ − q ∗ ) 2 = n q ∗ ( 1 − q ∗ ) ( p ∗ − q ∗ ) 2 + n π ( 1 − p ∗ − q ∗ ) p ∗ − q ∗ Var(\tilde c) = Var(\frac{{{n_1} - {q^*}n}}{{{p^*} - {q^*}}}) = \frac{{Var({n_1})}}{{{{({p^*} - {q^*})}^2}}} = \frac{{n\pi {p^*}(1 - {p^*}) + n(1 - \pi ){q^*}(1 - {q^*})}}{{{{({p^*} - {q^*})}^2}}}{\text{ = }}\frac{{n\pi {p^*} - n\pi {p^*}^2 + n{q^*}(1 - {q^*}) - n\pi {q^*} + n\pi {q^{*2}}}}{{{{({p^*} - {q^*})}^2}}} = \frac{{n{q^*}(1 - {q^*})}}{{{{({p^*} - {q^*})}^2}}} + \frac{{n\pi (1 - {p^*} - {q^*})}}{{{p^*} - {q^*}}} Var(c~)=Var(p∗−q∗n1−q∗n)=(p∗−q∗)2Var(n1)=(p∗−q∗)2nπp∗(1−p∗)+n(1−π)q∗(1−q∗) = (p∗−q∗)2nπp∗−nπp∗2+nq∗(1−q∗)−nπq∗+nπq∗2=(p∗−q∗)2nq∗(1−q∗)+p∗−q∗nπ(1−p∗−q∗)
当现实情况中,值域很大的情况。
或者p* + q* = 1 的情况。
V a r ( c ~ ) = n q ∗ ( 1 − q ∗ ) ( p ∗ − q ∗ ) 2 Var(\tilde c) = \frac{{n{q^*}(1 - {q^*})}}{{{{({p^*} - {q^*})}^2}}} Var(c~)=(p∗−q∗)2nq∗(1−q∗)
这里计算方差的方式细节和RR有一些不同:
3.Rappor
举一个不满足PureLDP的例子RAPPOR:
概率树公式为:
P [ S i = 1 ∣ B i = 1 ] = ( 1 − f 2 ) q + f 2 p = q ∗ P[{S_i} = 1|{B_i} = 1] = (1 - \frac{f}{2})q + \frac{f}{2}p = {q^*} P[Si=1∣Bi=1]=(1−2f)q+2fp=q∗
P [ S i = 0 ∣ B i = 0 ] = ( 1 − f 2 ) ( 1 − p ) + f 2 ( 1 − q ) = 1 − p ∗ P[{S_i} = 0|{B_i} = 0] = (1 - \frac{f}{2})(1 - p) + \frac{f}{2}(1 - q) = 1 - {p^*} P[Si=0∣Bi=0]=(1−2f)(1−p)+2f(1−q)=1−p∗
P [ S i = 1 ∣ B i = 0 ] = ( 1 − f 2 ) p + f 2 q = p ∗ P[{S_i} = 1|{B_i} = 0] = (1 - \frac{f}{2})p + \frac{f}{2}q = {p^*} P[Si=1∣Bi=0]=(1−2f)p+2fq=p∗
P [ S i = 0 ∣ B i = 1 ] = ( 1 − f 2 ) ( 1 − q ) + f 2 ( 1 − p ) = 1 − q ∗ P[{S_i} = 0|{B_i} = 1] = (1 - \frac{f}{2})(1 - q) + \frac{f}{2}(1 - p) = 1 - {q^*} P[Si=0∣Bi=1]=(1−2f)(1−q)+2f(1−p)=1−q∗
p*满足相等(真实扰动概率):
P ∗ [ y 1 ∣ P E ( v 1 ) ] = ( q ∗ ) 2 ( 1 − p ∗ ) 2 {P^*}[{y_1}|PE({v_1})] = {({q^*})^2}{(1 - {p^*})^2} P∗[y1∣PE(v1)]=(q∗)2(1−p∗)2
q*不满足相等(非真实扰动概率):
∀ v j ≠ v 1 Q ∗ [ y 1 ∣ P E ( v 2 ) ] = ( q ∗ ) ( p ∗ ) ( 1 − q ∗ ) ( 1 − p ∗ ) {\forall _{{v_j} \ne {v_1}}}{Q^*}[{y_1}|PE({v_2})] = ({q^*})({p^*})(1 - {q^*})(1 - {p^*}) ∀vj=v1Q∗[y1∣PE(v2)]=(q∗)(p∗)(1−q∗)(1−p∗)
Q ∗ [ y 1 ∣ P E ( v 3 ) ] = ( p ∗ ) 2 ( 1 − q ∗ ) 2 {Q^*}[{y_1}|PE({v_3})] = {({p^*})^2}{(1 - {q^*})^2} Q∗[y1∣PE(v3)]=(p∗)2(1−q∗)2
_2映射到_1的支持集的概率不等于_3映射到_1的支持集的概率所以RAPPOR不是Pure LDP Protocol
4.Direct Encoding
4.1GRR
Encoding:Encode(v)=v
Perturbation:GRR扰动
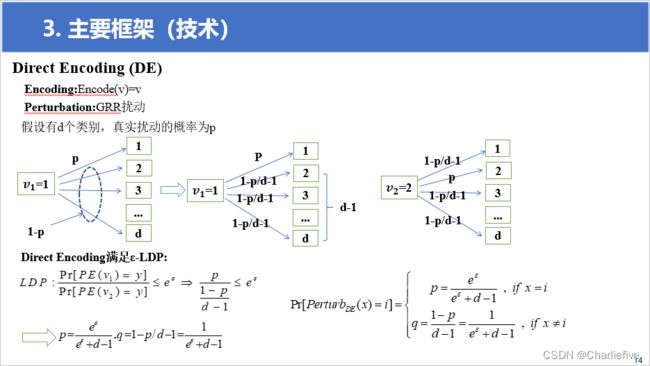
满足ε-LDP:
L D P : Pr [ P E ( v 1 ) = y ] Pr [ P E ( v 2 ) = y ] ⩽ e ε ⇒ p 1 − p d − 1 ⩽ e ε LDP:\frac{{\Pr [PE({v_1}) = y]}}{{\Pr [PE({v_2}) = y]}} \leqslant {e^\varepsilon } \Rightarrow \frac{p}{{\frac{{1 - p}}{{d - 1}}}} \leqslant {e^\varepsilon } LDP:Pr[PE(v2)=y]Pr[PE(v1)=y]⩽eε⇒d−11−pp⩽eε
p = e ε e ε + d − 1 , q = 1 − p / d − 1 = 1 e ε + d − 1 p = \frac{{{e^\varepsilon }}}{{{e^\varepsilon } + d - 1}},q = 1 - p/d - 1 = \frac{1}{{{e^\varepsilon } + d - 1}} p=eε+d−1eε,q=1−p/d−1=eε+d−11
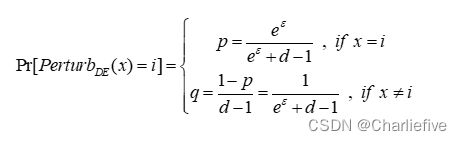
满足pureLDP:
从支持集角度来看
S u p p o r t ( y = 1 ) = { v 1 = 1 } Support(y = 1) = \{ {v_1} = 1\} Support(y=1)={v1=1}
l e t { y ∣ v 1 ∈ S u p p o r t D E ( y ) } = t let\;\{ y|{v_1} \in Suppor{t_{DE}}(y)\} = t let{y∣v1∈SupportDE(y)}=t
Pr [ P E ( v 1 ) ∈ t ] = p ∗ = p , ∀ v j ≠ v 1 Pr [ P E ( v j ) ∈ t ] = q ∗ = q \Pr [PE({v_1}) \in t] = {p^*} = p,{\forall _{{v_j} \ne {v_1}}}\Pr [PE({v_j}) \in t] = {q^*} = q Pr[PE(v1)∈t]=p∗=p,∀vj=v1Pr[PE(vj)∈t]=q∗=q
直接带入计算得出方差:
V a r ∗ ( c ~ D E ) = n e ε + d − 2 ( e ε − 1 ) 2 Var^*(\tilde{c}_{D E})\:=\:n\dfrac{e^{\varepsilon}+d\:-\:2}{\left(e^{\varepsilon}-1\right)^2} Var∗(c~DE)=n(eε−1)2eε+d−2
4.2RR
5.Unary Encoding
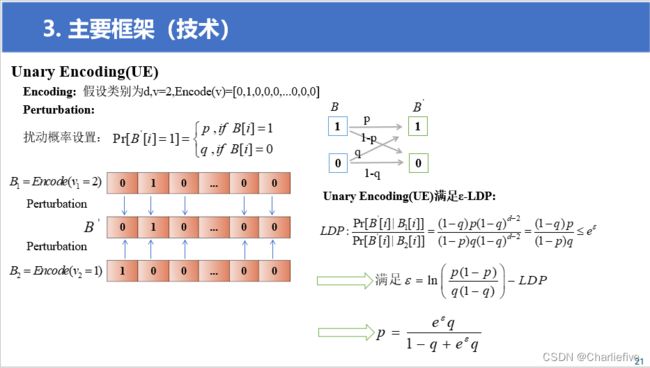
满足ε-LDP:
P : Pr [ B ∘ [ i ] ∣ B 1 [ i ] ] Pr [ B ∘ [ i ] ∣ B 2 [ i ] ] = ( 1 − q ) p ( 1 − q ) d − 2 ( 1 − p ) q ( 1 − q ) d − 2 = ( 1 − q ) p ( 1 − p ) q ≤ e ε P:\frac{\text{Pr}[\:B^{\circ}[i]\:|\:B_1[i]]}{\text{Pr}[\:B^{\circ}[i]\:|\:B_2[i]]}=\frac{\left(1-q\right)p\left(1-q\right)^{d-2}}{\left(1-p\right)q\left(1-q\right)^{d-2}}=\frac{\left(1-q\right)p}{\left(1-p\right)q}\leq\:e^{\varepsilon} P:Pr[B∘[i]∣B2[i]]Pr[B∘[i]∣B1[i]]=(1−p)q(1−q)d−2(1−q)p(1−q)d−2=(1−p)q(1−q)p≤eε
满足 ε = ln ( p ( 1 − p ) q ( 1 − q ) ) − L D P 满足\varepsilon = \ln \left( {{{p(1 - p)} \over {q(1 - q)}}} \right) - LDP 满足ε=ln(q(1−q)p(1−p))−LDP
p = e ε q 1 − q + e ε q p = {{{e^\varepsilon }q} \over {1 - q + {e^\varepsilon }q}} p=1−q+eεqeεq
满足pureLDP:
从支持集角度来看
S u p p o r t U E ( B ) = { i ∣ B [ i ] = 1 } Suppor{t_{UE}}(B) = \{ i|B[i] = 1\} SupportUE(B)={i∣B[i]=1}
S u p p o r t ( B 1 ) = { i ∣ B 1 [ i ] = 1 } = { v 1 } Support({B_1}) = \{ i|{B_1}[i] = 1\} = \{ {v_1}\} Support(B1)={i∣B1[i]=1}={v1}
l e t { B 1 ∣ v 1 ∈ S u p p o r t U E ( B 1 ) } = t let\;\{ {B_1}|{v_1} \in Suppor{t_{UE}}({B_1})\} = t let{B1∣v1∈SupportUE(B1)}=t
Pr [ P E ( v 1 ) ∈ t ] = p ∗ , ∀ v j ≠ v i Pr [ P E ( v j ) ∈ t ] = q ∗ \Pr [PE({v_1}) \in t] = {p^*},{\forall _{{v_j} \ne {v_i}}}\Pr [PE({v_j}) \in t] = {q^*} Pr[PE(v1)∈t]=p∗,∀vj=viPr[PE(vj)∈t]=q∗
直接带入计算得出方差:
只要满足PureLDP可以直接带入方差公式。
因为这个例子中p和q没什么联系,用其中一个未知数来表示方差。
V a r ∗ ( c ~ U E ) = n q ( 1 − q ) ( p − q ) 2 = n ( ( e ε − 1 ) q + 1 ) 2 ( e ε − 1 ) 2 + ( 1 − q ) q Va{r^*}({\tilde c_{UE}}) = {{nq(1 - q)} \over {{{(p - q)}^2}}} = n{{{{(({e^\varepsilon } - 1)q + 1)}^2}} \over {{{({e^\varepsilon } - 1)}^2} + (1 - q)q}} Var∗(c~UE)=(p−q)2nq(1−q)=n(eε−1)2+(1−q)q((eε−1)q+1)2
5.1Symmetric Unary Encoding
和UE类似。满足p+q=1,0和1是对称的
证明满足LDP和PureLDP的过程和前文类似,不作过多描述。
直接带入计算得出方差:
V a σ ∗ ( c ~ S L E ) = n 1 e σ 2 + 1 ( 1 − 1 e σ 2 + 1 ) ( e σ 2 e σ 2 + 1 − 1 e σ 2 + 1 2 = n e σ 2 ( e σ 2 − 1 ) 2 V a\sigma^{*}(\tilde{c}_{S L E})\:=\:n\frac{\frac{1}{e^{\sigma\:2}\:+\:1}(1\:-\frac{1}{e^{\sigma\:2}\:+\:1})}{(\frac{e^{\sigma\:2}}{e^{\sigma\:2}\:+\:1}-\frac{1}{e^{\sigma\:2}\:+\:1}^{2}}\:=\:n\frac{e^{\sigma\:2}}{(e^{\sigma\:2}\:-\:1)^{2}} Vaσ∗(c~SLE)=n(eσ2+1eσ2−eσ2+112eσ2+11(1−eσ2+11)=n(eσ2−1)2eσ2
5.1Optimized Unary Encoding
目的:方差最小化
满足p+q!=1

直接带入计算得出方差:
V a r ∗ ( c ~ U E ) = n q ( 1 − q ) ( p − q ) 2 = n ( ( e ε − 1 ) q + 1 ) 2 ( e ε − 1 ) 2 + ( 1 − q ) q Va{r^*}({\tilde c_{UE}}) = {{nq(1 - q)} \over {{{(p - q)}^2}}} = n{{{{(({e^\varepsilon } - 1)q + 1)}^2}} \over {{{({e^\varepsilon } - 1)}^2} + (1 - q)q}} Var∗(c~UE)=(p−q)2nq(1−q)=n(eε−1)2+(1−q)q((eε−1)q+1)2
上图对方差进行求偏导得到极值点求出p=1/2,下图用现实中极端假设的角度进行思考。
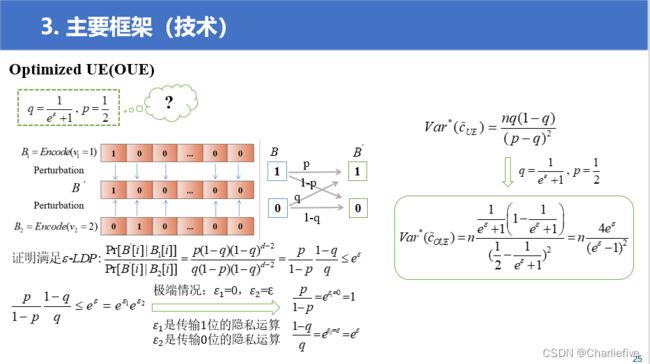
p 1 − p 1 − q q ≤ e ε = e ε 1 e ε 2 {p \over {1 - p}}{{1 - q} \over q} \le {e^\varepsilon } = {e^{{\varepsilon _1}}}{e^{{\varepsilon _2}}} 1−ppq1−q≤eε=eε1eε2
p 1 − p = e ε 1 = 0 = 1 且 1 − q q = e ε 2 = ε = e ε {p \over {1 - p}} = {e^{{\varepsilon _1} = 0}} = 1\; 且 {{1 - q} \over q} = {e^{{\varepsilon _2} = \varepsilon }} = {e^\varepsilon } 1−pp=eε1=0=1且q1−q=eε2=ε=eε
6.Local Hashing
目的:处理实际情况中, Encoding:(v)= p ∗ = p q ∗ = Pr [ H ( v ) = 1 ] Pr [ b ˙ ∗ = 1 ] + Pr [ H ( v ) = 0 ] Pr [ b ˙ ∗ = 1 ] = 1 2 p + 1 2 q = 1 2 \begin{array}{l}p^*=p\\ q^*=\Pr[H\left(v\right)=1]\Pr[\dot{b}^*=1]+\Pr[H\left(v\right)=0]\Pr[\dot{b}^*=1]\\ =\dfrac12p+\dfrac12q=\dfrac12\end{array} p∗=pq∗=Pr[H(v)=1]Pr[b˙∗=1]+Pr[H(v)=0]Pr[b˙∗=1]=21p+21q=21 直接带入计算得出 推广了BLH算法,将输入值哈希为[g]中的一个值, 直接带入计算得出 SHE不是PureLDP协议,因为每次每个值加的噪音服从的是Laplace分布,每次加的噪声可能是不一样的,因此每次非真实扰动的概率也可能是不同的。 此时不能通过Pure LDP的公式计算方差,应该按照概率密度函数来计算方差。 直接计算得出 这里p和q都和Laplace的累积分布函数有关,由参数决定, 直接计算得出 p ∗ = 1 − 1 2 e ε 2 ( θ − 1 ) , q ∗ = 1 2 e − ε 2 θ {p^*} = 1 - {1 \over 2}{e^{{\varepsilon \over 2}(\theta - 1)}},{q^*} = {1 \over 2}{e^{ - {\varepsilon \over 2}\theta }} p∗=1−21e2ε(θ−1),q∗=21e−2εθ V a r ∗ [ c ~ T H E ( i ) ] = n 2 e ε θ 2 − 1 ( 1 + e ε ( θ − 1 2 ) − 2 e − ε θ 2 ) 2 Va{r^*}[{\tilde c_{THE}}(i)] = n{{2{e^{{{\varepsilon \theta } \over 2}}} - 1} \over {{{(1 + {e^{\varepsilon (\theta - {1 \over 2})}} - 2{e^{ - {{\varepsilon \theta } \over 2}}})}^2}}} Var∗[c~THE(i)]=n(1+eε(θ−21)−2e−2εθ)22e2εθ−1编码太长,使用值域,降低通讯代价。通过hash的方式
HE和UE都使用一元编码,通信代价为O(d),当值域很大时,通信代价也很大
为了减少通信代价,将值哈希到k6.1Binary Local Hashing
H为哈希函数,b=H(v),只能哈希为0或1,等于hash之后的值域只为0或1
满足ε-LDP:
p*概率为真实扰动:
p*=p。
q*先考虑Encoding的时候,任何值x!=y,有一半概率映射为0,有一半概率映射为1.方差:
V a r ∗ ( c ~ B H ( l ) ) = n 1 / 4 ( e ε e ε + 1 − 1 2 ) 2 = n ( e ε + 1 ) 2 ( e ε − 1 ) 2 V a r^{*}(\tilde{c}_{B H}(l))=n\frac{1/4}{(\frac{e^{\varepsilon}}{e^{\varepsilon}+1}-\frac{1}{2})^{2}}=n\frac{(e^{\varepsilon}+1)^{2}}{(e^{\varepsilon}-1)^{2}} Var∗(c~BH(l))=n(eε+1eε−21)21/4=n(eε−1)2(eε+1)26.2Local Hashing
[g]≥2
Encoding:Encode(v)=

满足ε-LDP:
L D P : Pr [ < H , y > ∣ v 1 ] Pr [ < H , y > ∣ v 2 ] = Pr [ P e r t u r b ( H ( v 1 ) ) = y ] Pr [ P e r t u r b ( H ( v 2 ) ) = y ] ≤ e ε LDP:{{\Pr [ < H,y > |{v_1}]} \over {\Pr [ < H,y > |{v_2}]}} = {{\Pr [Perturb(H({v_1})) = y]} \over {\Pr [Perturb(H({v_2})) = y]}} \le {e^\varepsilon } LDP:Pr[<H,y>∣v2]Pr[<H,y>∣v1]=Pr[Perturb(H(v2))=y]Pr[Perturb(H(v1))=y]≤eε
⇒ p 1 − p g − 1 ≤ e ε ⇒ p = e ε e ε + g − 1 , q = 1 − p g − 1 = 1 e ε + g − 1 \Rightarrow {p \over {{{1 - p} \over {g - 1}}}} \le {e^\varepsilon } \Rightarrow p = {{{e^\varepsilon }} \over {{e^\varepsilon } + g - 1}},q = {{1 - p} \over {g - 1}} = {1 \over {{e^\varepsilon } + g - 1}} ⇒g−11−pp≤eε⇒p=eε+g−1eε,q=g−11−p=eε+g−11满足pureLDP:
支持函数: S u p p o r t L H ( < H , y > ) = { i ∣ H ( i ) = y } 支持函数:Suppor{t_{LH}}( < H,y > ) = \{ i|H(i) = y\} 支持函数:SupportLH(<H,y>)={i∣H(i)=y}
假设 v 1 = 1 , H ( v 1 ) = y = 1 , l e t S u p p o r t ( < H , y > ) = { v 1 ∣ H ( v 1 ) = y } = t 假设{v_1} = 1,H({v_1}) = y = 1,let\;Support( < H,y > ) = \{ {v_1}|H({v_1}) = y\} = t 假设v1=1,H(v1)=y=1,letSupport(<H,y>)={v1∣H(v1)=y}=t
Pr ( P E ( v 1 ) ∈ t ) = p ∗ = p , Pr ( P E ( ∀ v j ≠ v 1 ) ∈ t ) = q ∗ \Pr (PE({v_1}) \in t) = {p^*} = p,\Pr (PE({\forall _{{v_j} \ne {v_1}}}) \in t) = {q^*} Pr(PE(v1)∈t)=p∗=p,Pr(PE(∀vj=v1)∈t)=q∗每个p*或者q*都是独立且相等,同时p* > q*,因此满足。

方差:
V a r ( c ~ L H ( i ) ) = n 1 g ( 1 − 1 g ) ( e s e s + g − 1 − 1 g ) 2 = n ( e s + g − 1 ) 2 ( e s − 1 ) 2 ( g − 1 ) V a r(\tilde{c}_{L H}(i))=n\frac{\frac{1}{g}(1-\frac{1}{g})}{(\frac{e^{s}}{e^{s}+g-1}-\frac{1}{g})^{2}}=n\frac{(e^{s}+g-1)^{2}}{(e^{s}-1)^{2}(g-1)} Var(c~LH(i))=n(es+g−1es−g1)2g1(1−g1)=n(es−1)2(g−1)(es+g−1)26.3Optimal Local Hashing

直接极值点带入计算得出方差:
V a r ( c ~ o L H ( i ) ) = n 4 e ε ( e ε − 1 ) 2 V a r(\tilde{c}_{o L H}\left(i\right))=n\frac{4e^{\varepsilon}}{\left(e^{\varepsilon}-1\right)^{2}} Var(c~oLH(i))=n(eε−1)24eε7.Histogram Encoding
7.1Summation with Histogram Encoding不纯
方差:
每个值付出尺度参数为b的Laplace分布

7.2Thresholding with Histogram Encoding
满足pureLDP:
θ = 1 , S u p p o r t ( B ) = { v ∣ B [ v ] > 1 } \theta {\rm{ = }}1\;,Support(B) = \{ v|B[v] > 1\} θ=1,Support(B)={v∣B[v]>1}
S u p p o r t ( B 1 ) = { v ∣ B 1 [ v ] > 1 } = { v 1 } Support({B_1}) = \{ v|{B_1}[v] > 1\} = \{ {v_1}\} Support(B1)={v∣B1[v]>1}={v1}
l e t { v 1 ∣ B 1 [ v 1 ] > 1 } = t let\;\{ {v_1}|{B_1}[{v_1}] > 1\} = t let{v1∣B1[v1]>1}=t
Pr [ P E ( v 1 ) ∈ t ] = p ∗ , ∀ v j ≠ v 1 Pr [ P E ( v j ) ∈ t ] = q ∗ \Pr [PE({v_1}) \in t] = {p^*},{\forall _{{v_j} \ne {v_1}}}\Pr [PE({v_j}) \in t] = {q^*} Pr[PE(v1)∈t]=p∗,∀vj=v1Pr[PE(vj)∈t]=q∗参数定了以后概率也是一样的,因此满足PureLDP分布。方差:
V a r ∗ ( c ~ ) = n q ∗ ( 1 − q ∗ ) ( p ∗ − q ∗ ) 2 Va{r^*}(\tilde c) = {{n{q^*}(1 - {q^*})} \over {{{({p^*} - {q^*})}^2}}} Var∗(c~)=(p∗−q∗)2nq∗(1−q∗)