两篇2023 ICLR多模态论文分享(模态互补性对多模态鲁棒性影响 与 对多模表示学习有效的单模学习)

Modality Complementariness Towards Understanding Multi modal Robustness

本文讨论了模态互补性在多模态鲁棒性中的重要性，并基于信息论提出了一种数据集层面量化度量，用于量化不同模态之间有多少互补信息，以及这些信息对预测标签有多大贡献。该指标基于互信息神经估计器（MINE）来计算。提出了一个两阶段pipeline，分成数据生成阶段和度量计算阶段。在数据生成阶段，作者生成具有受控模态互补性的数据集。在度量计算阶段，作者使用生成的数据集计算度量并分析结果。，并通过实验验证了其有效性。此外，本文还讨论了各种相关主题，如变压器、对抗性示例和深度学习模型。
这篇论文的主要贡献是提供了一个统一且可操作的方法来评估和优化多模态学习系统，以及提出了一些有趣且具有启发性的发现，例如：不同任务下最佳模态组合可能不同；单一模态可能包含足够或过剩信息；增加噪声或缺失值可以提高某些情况下的互补性等。本文还为量化多模态和缺失模态或噪声模态的贝叶斯错误率之间的差异提供了理论保证。

这篇论文的局限性或未来方向有：
这篇论文的理论分析框架只适用于多模态分类任务，对于其他类型的多模态任务，如生成、检索、对话等，还需要进一步扩展和验证。
这篇论文的指标计算依赖于互信息神经估计器（MINE），而MINE本身可能存在一些问题，如估计偏差、不稳定性、超参数敏感性等，这些问题可能影响到指标的准确性和可靠性。
这篇论文的实验设置较为简单，只考虑了两种模态（视觉和语言）以及两种噪声类型（高斯噪声和缺失值），对于更复杂和更真实的多模态场景，还需要进行更多的探索和分析。
互信息神经估计器（MINE）是一种基于神经网络的方法，用于估计高维连续随机变量之间的互信息。互信息是衡量两个随机变量之间相关性的一个指标，它等于两个随机变量的联合分布与边缘分布之间的KL散度1。MINE利用了一个重要的定理，即最大化一个函数关于联合分布和边缘分布的期望差等价于最大化该函数与互信息之间的下界23。因此，MINE可以通过梯度下降来训练一个神经网络，使其输出接近互信息的下界，并且具有线性可扩展性、灵活性和强一致性。
MINE的优势有：

它可以有效地估计高维连续随机变量之间的互信息，而不需要对分布做任何假设或近似。
它可以通过梯度下降来训练一个神经网络，使其输出接近互信息的下界，而不需要计算复杂的积分或优化问题。
它具有线性可扩展性、灵活性和强一致性，即它可以处理任意维度和样本大小的数据，并且在样本趋于无穷时，它的估计值会收敛到真实值。
MINE的缺点有：

它依赖于一个超参数，即神经网络的结构和激活函数，这些选择可能影响到估计值的准确性和稳定性。
它可能存在一些估计偏差，即它的估计值可能低于或高于真实值，这取决于神经网络的初始化和训练过程。
它可能受到样本相关性、噪声、离群点等因素的干扰，导致估计值不准确或不可靠。
有很多方法可以估计互信息，其中一些常见的有：

直接方法：这种方法通过呈现来自p(S)的刺激，并从重复呈现相同刺激来估计hΔ(R|S)，从而估计hΔ®和hΔ(R|S)。由于估计p(R|S)所需的数据量通常很大，因此大多数研究者采用一些技术来给I(S;R)设置上下界。
基于k最近邻的方法：这种方法通过利用k最近邻距离来估计熵和互信息，不需要对数据进行分箱或假设分布的形式。它具有非参数性、鲁棒性和一致性，但也存在一些缺点，如高维空间中距离度量的困难、超参数k的选择和样本相关性的影响。
基于几何k最近邻的方法：这种方法是基于k最近邻的方法的改进，它通过在流形上定义距离度量来克服高维空间中欧氏距离失效的问题。它利用了流形学习中的局部线性嵌入（LLE）算法，将数据映射到一个低维空间，然后在该空间中使用k最近邻算法来估计互信息。、

论文的3.1节主要讲了多模态互补性度量（Modality Complementarity Metric），这是一个用来评估多模态数据中不同模态之间信息互补程度的指标。该指标基于信息熵（Entropy）和互信息（Mutual Information）的概念，可以反映出多模态数据中每个模态对整体信息的贡献和冗余。该指标可以用来预测多模态模型在不同场景下的鲁棒性，例如缺失某个模态、某个模态受到噪声或对抗攻击等
论文的3.2节主要讲了多模态互补性度量的理论分析（Theoretical Analysis of Modality Complementarity Metric），这是一个用来证明该指标与多模态鲁棒性之间关系的数学推导。该分析基于贝叶斯风险（Bayesian Risk）和最小化期望损失（Minimizing Expected Loss）的原则，给出了在不同场景下，多模态互补性度量与多模态模型性能之间的上下界。该分析表明，当某个模态缺失或受到噪声或对抗攻击时，多模态互补性度量越高，多模态模型的性能下降越小。
这篇论文的3.3节主要讨论了如何在真实世界的多模态数据集上计算模态互补性度量，并展示了不同数据集的模态互补性和多模态鲁棒性之间的关系。

论文中的图2显示了在不同设置下，模态互补性和多模态鲁棒性之间的关系。模态互补性是一种度量每种模态对其他模态增加多少信息的指标。多模态鲁棒性是指一个模型在某些模态缺失或受损时能够表现良好的能力。

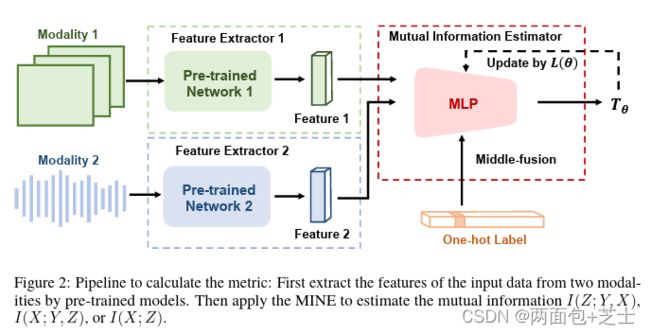
图2的作用是说明论文的主要思想：模态互补性影响多模态鲁棒性。互补性越高，模型对缺失或噪声模态越敏感。互补性越低，模型对这种情况越鲁棒 。
I(X; Y, Z)表示X和(Y, Z)之间的互信息，即X减少了对(Y, Z)的不确定性的程度。它等于(Y, Z)的熵减去给定X时(Y, Z)的熵。
I(Z; Y, X) 表示 Z 和 (Y, X) 之间的模态互补性，即 Z 在 (Y, X) 缺失或受损时能够减少对 (Y, X) 的不确定性的程度。它等于 (Y, X) 的熵减去给定 Z 时 (Y, X) 的熵。
I(X; Y, Z) 表示给定 (Y, Z) 时 X 的多模态鲁棒性，即 X 在 (Y, Z) 存在且可靠时能够减少对 (Y, Z) 的不确定性的程度。它等于 (Y, Z) 的熵减去给定 X 时 (Y, Z) 的熵。

4.2节主要讲了一种用于计算模态互补性度量的实用流程。该流程包括三个步骤：1) 使用互信息神经估计器 (MINE) (Belghazi et al., 2018) 来估计不同模态之间的互信息；2) 使用条件熵神经估计器 (CENE) 来估计给定一个或多个模态时，另一个模态的条件熵；3) 使用公式 (4) 来计算模态互补性度量。该流程可以处理任意数量和类型的模态，并且可以在真实世界的多模态数据集上运行。

公式 (4) 定义了模态互补性度量 (MCM) 作为不同模态之间的互信息和条件熵的函数。MCM 可以看作是一个模态在其他模态缺失或受损时能够提供的有用信息的比例。MCM 的值越高，表示一个模态对其他模态的补充程度越高，也就意味着多模态模型在面对缺失或噪声干扰时更容易受到影响。
这种方法的目的是为了定量地评估多模态数据集中不同模态之间的互补性，从而揭示互补性对多模态模型鲁棒性的影响。作者认为，现有的多模态学习理论和实践中忽略了这一重要因素，导致了一些矛盾的结论。因此，他们提出了一个基于信息论的分析框架和一个基于神经网络估计器的计算流程，来探索互补性在不同任务和数据集上的变化，并与多模态模型在缺失、噪声和对抗攻击等情况下的表现进行比较。

On Uni modal Feature Learning in Multi modal Learning

多模态数据的特征抽象为1)单模态特征(可以从单模态训练中学习)和2)配对特征(只能从跨模态交互中学习)。多模态联合训练有望在保证单模态特征学习的基础上受益于跨模态交互。然而，目前的后期融合训练方法仍然存在对每个模态上的单模态特征学习不足的问题，并且证明了这一现象确实损害了模型的泛化能力。针对一个多模态任务，根据单模态和成对特征的分布，从单模态集成(UME)和提出的单模态教师(UMT)中选择有针对性的后期融合学习方法。我们证明，在一个简单的指导策略下，我们可以在多模态数据集上获得与其他复杂的后期融合或中间融合方法
单模态先验有意义的多模态任务。理想情况下，我们希望多模态联合训练能够在保证学习足够多的单模态特征的基础上，通过跨模态交互来学习成对特征。

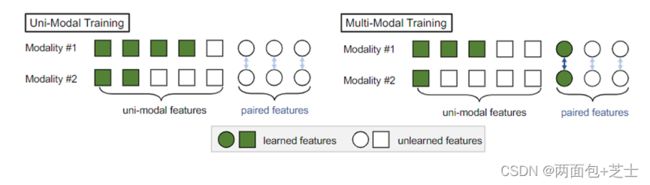
虽然多模态联合训练为跨模态交互提供了学习配对特征的机会，但该模型容易饱和并忽略了难以学习但对泛化很重要的单模态特征
然而，最近的后期融合方法仍然存在学习每个模态的单模态表示不足的问题。我们将这种现象称为模态懒惰，并在图1中加以说明。我们从理论上描述了模态懒惰，并证明它确实损害了模型的泛化能力，特别是当单模态特征在给定任务中占主导地位时。
我们关注单模态特征的学习，根据单模态特征和配对特征的分布，从Uni-ModalEnsemble (UME)和提出的uni-modal Teacher (UMT)中选择有针对性的后期融合训练方法。如果单模态特征和成对特征都是必要的，则UMT是有效的，它可以帮助多模态模型通过单模态蒸馏更好地学习单模态特征;如果两种模态都具有较强的单模态特征，且成对特征不够重要，则采用UME，它结合了单模态模型的预测，完全避免了对单模态特征的学习不足。我们还提供了一个经验技巧来决定使用哪一个。
联合训练优缺点：一方面，联合训练导致单模态特征学习不足(Modality lazy)。另一方面，它允许模态之间的交互，以学习单模态特征以外的表示，即成对特征。基于此，我们提供了多模态后期融合学习的指导。最后，我们对情态懒惰进行了理论分析，并对我们的解决方案进行了论证。
视觉问答(VQA) (Agrawal等人，2018)是一个反例。具体来说，相同的图像与不同的文本问题可能有完全不同的标签，使得检查其单模态准确性毫无意义。

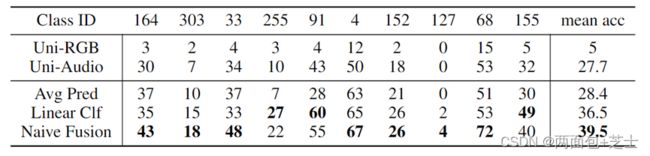
对单模态模型的预测结果进行平均，预训练的单模态编码器上训练一个多模态线性分类器，其中模态可以通过线性层相互作用，朴素融合，没有使用精心设计的技巧 跨模态交互作用。

对于一个多模态任务，如果单模态特征和配对特征都是必要的，那么Uni-ModalTeacher (UMT)是有效的;如果两种模态都具有强烈的单模态特征，同时成对特征不重要，简单地结合单模态模型的预测就可以很好地实现，这种方法被称为单模态集成(UME)。

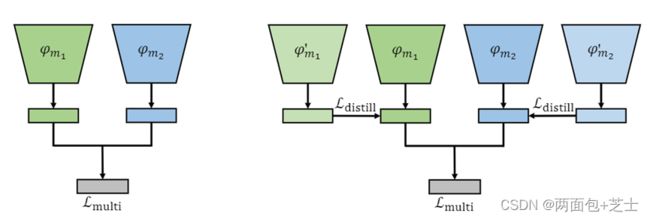
φ′miis是对单模态数据进行监督预训练的编码器。φmi是一个没有预训练的随机初始编码器。Lmulti是多模态预测和标签之间的损失。Ldistill是单模态蒸馏损失。
单模态蒸馏发生在融合前，late-fusion
从单模态模型中提取知识可以帮助多模态模型更好地学习单模态特征，这发生在特征级。UMT的框架如图1和图4所示。请注意，对于特定的模态，我们在单模态模型和多模态模型中使用相同的backbone。
如果两种模式都有强烈的单模态特征，联合训练弊大于利。结合单模态模型的预测，避免了单模态特征的学习不足。首先，我们可以独立地训练单模态模型。然后，我们可以通过加权单模态模型的预测给出最终输出。简单的集成方法被称为单模态集成(UME)。我们证明了UME可以在某些多模态数据集上表现出具有竞争力的性能。
决定使用哪种方法的经验Trick。我们可以在单模态预训练编码器上训练一个多模态线性分类器，并将其与单模态模型的平均预测进行比较。如果分类器的性能更好，则意味着我们可以从该任务中的跨模态交互中受益，我们可以选择UMT，在保证改善单模态特征学习的同时，保留跨模态交互;反之，简单的跨模态交互弊大于利，因为每个模态都有很强的单模态特征，我们可以选择UME，它完全避免了模态懒惰。
证明：从特征学习角度证明模态惰性确实对多模态的泛化性有害
多模态联合训练可以比单模态训练学习更多的特征，但所学习的特征不一定有用，甚至会损害模型的泛化。定理3.4指出，在单模态集成中，与单模态训练相比，训练过程学习到的单模态特征更少，这损害了模型的泛化。这种现象被称为模态懒惰

UMT，Bm1特征学自模态xm1，在多模态训练方法中，假设训练程序在模态x m1中学习了km1的单模态特征，在模态x m2中学习了km2的单模态特征，并学习了kpa的配对特征
考虑一个新的测试点，然后对于每个 δ > 0，如果以下不等式成立：
其中 ∆(δ) = p 8(kpa + bm1 − km1 + bm2 − km2) log(1/δ)，则概率 至少为 1 − δ，单模态集成优于多模态训练方法概率测试点
数量懒惰表示在简单的多模态训练中学习到的特征数量少于单模态训练。
单模态懒惰表明，由于数量懒惰，多模态训练的编码器比单模态训练的编码器性能差，这符合第3.1节的实验结果。
性能懒惰比较了多模态联合训练方法和单模态集合的性能，表明当单模态特征占主导地位时，结合单模态的预测更有效。