剑指 Offer （第 2 版）

（简单）剑指 Offer 03. 数组中重复的数字

找出数组中重复的数字。

在一个长度为 n 的数组 nums 里的所有数字都在 0～n-1 的范围内。数组中某些数字是重复的，但不知道有几个数字重复了，也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。

示例 1：

输入：
[2, 3, 1, 0, 2, 5, 3]
输出：2 或 3 

限制：

2 <= n <= 100000

题解：

• C++

class Solution {
public:
    int findRepeatNumber(vector<int>& nums) {
        int i = 0;
        while(i < nums.size())
        {
            if (nums[i] == i)
            {
                i++;
                continue;
            }
            if (nums[i] == nums[nums[i]])
                return nums[i];
            swap(nums[i], nums[nums[i]]);
        }
        return -1;
    }
};

• Golang

func findRepeatNumber(nums []int) int {
    length := len(nums);
    i := 0

    for i < length {
        if nums[i] == i {
            i++
            continue
        }

        if nums[i] == nums[nums[i]] {
            return nums[i]
        }

        nums[i], nums[nums[i]] = nums[nums[i]], nums[i]
    }

    return -1
}

（中等）剑指 Offer 04. 二维数组中的查找

减 的顺序排序。请完成一个高效的函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

示例:

现有矩阵 matrix 如下：

[
  [1,   4,  7, 11, 15],
  [2,   5,  8, 12, 19],
  [3,   6,  9, 16, 22],
  [10, 13, 14, 17, 24],
  [18, 21, 23, 26, 30]
]

给定 target = 5，返回 true。

给定 target = 20，返回 false。

限制：

0 <= n <= 1000

0 <= m <= 1000

题解：

• C++

class Solution {
public:
    bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) 
    {
        if (matrix.size() <= 0)
            return false;

        int i = matrix.size() - 1;
        int j = 0;
        while (i >= 0 && j < matrix[0].size())
        {
            if (target < matrix[i][j])
                i--;
            else if (target > matrix[i][j])
                j++;
            else 
                return true;
        };
        return false;
    }
};

• Golang

func findNumberIn2DArray(matrix [][]int, target int) bool {
    rows := len(matrix)
    if rows < 1 {
        return false
    }

    cols := len(matrix[0])

    i := rows - 1
    j := 0

    for i >= 0 && j < cols {
        if target < matrix[i][j] {
            i--
        } else if target > matrix[i][j] {
            j++
        } else {
            return true
        }
    }

    return false
}

（简单）剑指 Offer 05. 替换空格

请实现一个函数，把字符串 s 中的每个空格替换成"%20"。

示例 1：

输入：s = "We are happy."
输出："We%20are%20happy."

限制：

0 <= s 的长度 <= 10000

题解：

• C++

class Solution {
public:
    string replaceSpace(string s) {
        int count = 0;

        for(auto ch: s)
            if (ch == ' ')
                count++;
        int len = s.size();
        s.resize(len + 2 * count);
        
        for (int i = len - 1, j = s.size() - 1; i < j; i--, j--)
            if (s[i] != ' ')
                s[j] = s[i];
            else
            {
                s[j] = '0';
                s[j - 1] = '2';
                s[j - 2] = '%';
                j -= 2;
            }
        return s;
    }
};

• Golang

func replaceSpace(s string) string {
    ss := []byte(s)
    length := len(ss)
    count := 0
    for _, ch := range ss {
        if ch == ' ' {
            count++
        }
    }

    cmp := make([]byte, 2 * count)
    ss = append(ss, cmp...)

    for i, j := length - 1, len(ss) - 1; i < j; i, j = i - 1, j - 1 {
        if ss[i] != ' ' {
            ss[j] = ss[i]
        } else {
           ss[j] = '0'
           ss[j - 1] = '2'
           ss[j - 2] = '%'
           j -= 2 
        }
    }

    return string(ss)
}

（简单）剑指 Offer 06. 从尾到头打印链表

输入一个链表的头节点，从尾到头反过来返回每个节点的值（用数组返回）。

示例 1：

输入：head = [1,3,2]
输出：[2,3,1]

限制：

0 <= 链表长度 <= 10000

题解：

• C++

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> reversePrint(ListNode* head) {
        std::vector<int> res;

        while(head)
        {
            res.push_back(head->val);
            head = head->next;
        }
        
        int n = res.size();
        for (int i = 0; i < (n >> 1); i++)
           swap(res[i], res[n - 1 -i]);
           
        return res;
    }
};

• Golang

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func reversePrint(head *ListNode) []int {
    v := make([]int, 0)

    for head != nil {
        v = append(v, head.Val)
        head = head.Next
    }

    length := len(v)

    for i := 0; i < length / 2; i++ {
        v[i], v[length - 1 - i] = v[length - 1 - i], v[i]
    }

    return v
}

（中等）剑指 Offer 07. 重建二叉树

输入某二叉树的前序遍历和中序遍历的结果，请构建该二叉树并返回其根节点。

假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

示例 1:

Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

示例 2:

Input: preorder = [-1], inorder = [-1]
Output: [-1]

限制：

0 <= 节点个数 <= 5000

题解：

• C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
private:
    std::unordered_map<int, int> m_index;
    TreeNode* _buildTree(std::vector<int>& preorder, int preLeft, int preRight,
               std::vector<int>& inorder , int inLeft , int inRight)
    {
        if (preLeft > preRight)
            return nullptr;

        int rootValue = preorder[preLeft];
        TreeNode* root = new TreeNode(rootValue);
        
        // root node value in inorder.
        int index = m_index[rootValue];
        // length of left subtree.
        int length = index - inLeft; // (index -1) - inLeft + 1 

        root->left = _buildTree(preorder, preLeft + 1, (preLeft + 1) + (length - 1),
                                 inorder, inLeft, index - 1);
        root->right = _buildTree(preorder, (preLeft + 1) + length, preRight,
                                 inorder, index + 1, inRight);

        return root;
    }
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) 
    {
        int n = preorder.size();

        for (int i = 0; i < n; i++)
            m_index[inorder[i]] = i;

        return _buildTree(preorder, 0, n -1, inorder , 0, n -1);
    }
};

• Golang

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */

func buildTreeInternal(preorder, inorder []int, preLeft, preRight, inLeft, inRight int, indexMap map[int]int) *TreeNode {
    if preLeft > preRight {
        return nil
    }

    rootValue := preorder[preLeft]
    index := indexMap[rootValue]
    root := &TreeNode{rootValue, nil, nil}
    length := index - inLeft

    root.Left = buildTreeInternal(preorder, inorder, preLeft + 1, preLeft + length, inLeft, index - 1, indexMap)
    root.Right = buildTreeInternal(preorder, inorder, preLeft + length + 1, preRight, index + 1, inRight, indexMap)

    return root;
}

func buildTree(preorder []int, inorder []int) *TreeNode {
    n := len(preorder)
    indexMap := map[int]int{}

    for i, v := range inorder {
        indexMap[v] = i
    }

    return buildTreeInternal(preorder, inorder, 0, n - 1, 0, n - 1, indexMap)
}

（简单）剑指 Offer 09. 用两个栈实现队列

用两个栈实现一个队列。队列的声明如下，请实现它的两个函数 appendTail 和 deleteHead ，分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素，deleteHead 操作返回 -1 )

示例 1：

输入：

["CQueue","appendTail","deleteHead","deleteHead","deleteHead"]
[[],[3],[],[],[]]
输出：[null,null,3,-1,-1]

示例 2：

输入：
["CQueue","deleteHead","appendTail","appendTail","deleteHead","deleteHead"]
[[],[],[5],[2],[],[]]
输出：[null,-1,null,null,5,2]

提示：

• 1 <= values <= 10000
• 最多会对 appendTail、deleteHead 进行 10000 次调用

题解：

• C++

class CQueue {
private:
    std::stack<int> m_stackA, m_stackB;
    void moveA2B() {
        while(!m_stackA.empty()){
            m_stackB.push(m_stackA.top());
            m_stackA.pop();
        }
    }
public:
    CQueue() {

    }
    
    void appendTail(int value) {
        m_stackA.push(value);
    }
    
    int deleteHead() {
        if (m_stackB.empty()) {
            if (m_stackA.empty())
                return -1;
            moveA2B();
        }

        int result = m_stackB.top();
        m_stackB.pop();
        
        return result;
    }
};

/**
 * Your CQueue object will be instantiated and called as such:
 * CQueue* obj = new CQueue();
 * obj->appendTail(value);
 * int param_2 = obj->deleteHead();
 */

• Golang

type CQueue struct {
    inStack, outStack []int
}


func Constructor() CQueue {
    return CQueue{}
}

func (this *CQueue)moveStack() {
    for len(this.inStack) != 0 {
        this.outStack = append(this.outStack, this.inStack[len(this.inStack) - 1])
        this.inStack = this.inStack[:len(this.inStack) - 1]
    }
}

func (this *CQueue) AppendTail(value int)  {
    this.inStack = append(this.inStack, value)
}


func (this *CQueue) DeleteHead() int {
    if len(this.outStack) == 0 {
        if len(this.inStack) == 0 {
            return -1
        }

        this.moveStack()
    }

    r := this.outStack[len(this.outStack) - 1]
    this.outStack = this.outStack[:len(this.outStack) - 1]

    return r
}


/**
 * Your CQueue object will be instantiated and called as such:
 * obj := Constructor();
 * obj.AppendTail(value);
 * param_2 := obj.DeleteHead();
 */

（简单）剑指 Offer 10- I. 斐波那契数列

写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项（即 F(N)）。斐波那契数列的定义如下：

F(0) = 0,   F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.

斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

示例 1：

输入：n = 2
输出：1

示例 2：

输入：n = 5
输出：5

提示：

0 <= n <= 100

题解：

• C++

class Solution {
public:
    int fib(int n) {
        if (n < 2)
            return n;

        int a = 0, b = 1, sum = 0;
        for (int i = 2; i <= n ; i++)
        {
            sum = (a + b) % 1000000007;
            a = b;
            b = sum;
        }

        return sum ;
    }
};

• Golang

func fib(n int) int {
    if n < 1 {
        return 0
    }

    if n == 1 {
        return 1
    } 

    sum := 0
    a, b := 0, 1

    for i := 2; i <= n; i++ {
        sum = (a + b) % 1000000007
        a = b
        b = sum
    }

    return sum
}

（简单）剑指 Offer 10- II. 青蛙跳台阶问题

一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

示例 1：

输入：n = 2
输出：2

示例 2：

输入：n = 7
输出：21

示例 3：

输入：n = 0
输出：1

提示：

0 <= n <= 100

题解：

• C++

class Solution {
public:
    int numWays(int n) {
        if (n == 0) 
            return 1;
        if (n == 1)
            return 1;
        int a  = 1, b = 1, r = 0;
        for (int i = 2; i <= n; i++)
        {
            r = (a + b)%1000000007;
            a = b;
            b = r;
        }

        return r;
    }
};

• Golang

func numWays(n int) int {
    if n == 0 {
        return 1
    }
    if n == 1 {
        return 1
    }

    a, b := 1, 1
    sum := 0
    for i := 2; i <= n; i++ {
        sum = (a + b) % 1000000007
        a, b = b, sum
    }

    return sum
}

（简单）剑指 Offer 11. 旋转数组的最小数字

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。

给你一个可能存在 重复 元素值的数组 numbers ，它原来是一个升序排列的数组，并按上述情形进行了一次旋转。请返回旋转数组的最小元素。例如，数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一次旋转，该数组的最小值为 1。

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

示例 1：

输入：numbers = [3,4,5,1,2]
输出：1

示例 2：

输入：numbers = [2,2,2,0,1]
输出：0

提示：

• n == numbers.length
• 1 <= n <= 5000
• -5000 <= numbers[i] <= 5000
• numbers 原来是一个升序排序的数组，并进行了 1 至 n 次旋转

题解：

• C++

class Solution {
public:
    int minArray(vector<int>& numbers) {
        int low = 0;
        int high  = numbers.size() - 1;

        while (low < high)
        {
            int pivot = low + ((high - low) >> 1);
            if (numbers[pivot] < numbers[high])
                high = pivot;
            else if (numbers[pivot] > numbers[high])
                low = pivot + 1;
            else 
                high--;
        }

        return numbers[low];
    }
};

• Golang

func minArray(numbers []int) int {
    low := 0
    high := len(numbers) - 1
    for low < high {
        pivot := low + (high - low) / 2
        if numbers[pivot] < numbers[high] {
            high = pivot
        } else if numbers[pivot] > numbers[high] {
            low = pivot + 1
        } else {
            high--
        }
    }

    return numbers[low]
}

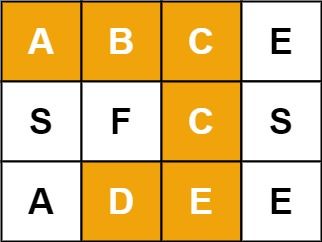
（中等）剑指 Offer 12. 矩阵中的路径

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

例如，在下面的 3×4 的矩阵中包含单词 “ABCCED”（单词中的字母已标出）。

示例 1：

输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true

示例 2：

输入：board = [["a","b"],["c","d"]], word = "abcd"
输出：false

提示：

• m == board.length
• n = board[i].length
• 1 <= m, n <= 6
• 1 <= word.length <= 15
• board 和 word 仅由大小写英文字母组成

题解：

• C++

class Solution {
private:
    int m_columns, m_rows;
    bool dfs(vector<vector<char>>& board, string word, int i, int j, int index)
    {
        if (i >= m_rows ||
            j >= m_columns ||
            i < 0 ||
            j < 0 ||
            board[i][j] != word[index])
            return false;
        
        if (index == word.size() - 1)
            return true;

        board[i][j] = '\0';

        bool result = dfs(board, word, i + 1, j, index + 1) || dfs(board, word, i - 1, j, index + 1) ||
                      dfs(board, word, i, j + 1, index + 1) || dfs(board, word, i, j - 1, index + 1);
        board[i][j] = word[index];

        return result;
    }

public:
    bool exist(vector<vector<char>>& board, string word) 
    {
        m_rows = board.size();
        m_columns = board[0].size();

        for (int i = 0; i < m_rows; i++)
            for (int j = 0; j < m_columns; j++)
                if (dfs(board, word, i, j, 0))
                    return true;

        return false;
    }
};

• Golang

func exist(board [][]byte, word string) bool {
    for i := range board {
        for j := range board[i] {
            if dfs(board, word, i, j, 0) {
                return true
            }
        }
    }

    return false
}

func dfs(board [][]byte, word string, i, j, index int) bool {
    if i < 0 || j < 0 || i >= len(board) || j >= len(board[0]) || board[i][j] != word[index] {
        return false
    }

    if index == len(word) - 1 {
        return true
    }
    
    board[i][j] = 0
    r := dfs(board, word, i + 1, j, index + 1) || 
        dfs(board, word, i - 1, j, index + 1) || 
        dfs(board, word, i, j + 1, index + 1) ||
        dfs(board, word, i, j - 1, index + 1)

    board[i][j] = word[index]
    return r
}

（中等）剑指 Offer 14- I. 剪绳子

给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]...k[m-1] 。请问 k[0]*k[1]*...*k[m-1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

示例 1：

输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1

示例 2:

输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36

提示：

• 2 <= n <= 58

题解：

• C++

class Solution {
public:
    int cuttingRope(int n) {
        if (n < 4)
            return n - 1;
        
        int a = n / 3;
        int b = n % 3;

        if (b == 0) {
            return pow(3, a);
        } else if (b == 1) {
            return pow(3, a - 1) * 4;
        } 

        return pow(3, a) * 2;
    }
};

• Golang

func cuttingRope(n int) int {
    if n < 4 {
        return n - 1
    }

    a := n / 3;
    b := n % 3;

    if b == 0 {
        return int(math.Pow(3, float64(a)))
    } else if b == 1 {
        return int(math.Pow(3, float64(a - 1)) * 4)
    }

    return int(math.Pow(3, float64(a)) * 2)
}

（中等）剑指 Offer 14- II. 剪绳子 II

给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]...k[m - 1] 。请问 k[0]*k[1]*...*k[m - 1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

示例 1：

输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1

示例 2:

输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36

提示：

• 2 <= n <= 1000

题解：

• C++

class Solution {
private:
    const int MOD = (int)1000000007;
   int mpow(long a, long b) {
       if (b < 1)
           return 1;
        
        long result = 1;
        while(b > 0) {
            if (b & 1)
               result = (a * result) % MOD;
            a = (a * a) % MOD;
            b >>= 1;
        }

        return result;
   }
public:
    int cuttingRope(int n) {
        if (n < 4)
           return n - 1;
        
        int a = n / 3;
        int b = n % 3;

        int result = 0;

        if (b == 0) {
            return (int)mpow(3, a) % MOD;
        } else if (b == 1) {
            return (int)((mpow(3, a - 1) * 4L) % MOD);
        } 
        
        return (int)((mpow(3, a) * 2L) % MOD);
    }
};

• Golang

var base, mod uint64 = 3, 1000000007

func cuttingRope(n int) int {
    if n < 4 {
        return n - 1;
    }

    exponent := uint64(n) / base
    remainder := uint64(n) % base

    if remainder == 0 {
        return int(mPow(base, exponent))
    } else if remainder == 1 {
        return int((mPow(base, exponent - 1) * uint64(4)) % mod)
    }

    return int((mPow(base, exponent) * uint64(2)) % mod)
}

func mPow(base, exponent uint64) uint64 {
    if exponent < 1 {
        return 1;
    }

    var result uint64 = 1

    for exponent > 0 {
        if (exponent & 1) > 0 {
            result = (result * base) % mod;
        }

        base = (base * base) % mod;

        exponent >>= 1
    }

    return result
}

（简单）剑指 Offer 15. 二进制中1的个数

编写一个函数，输入是一个无符号整数（以二进制串的形式），返回其二进制表达式中数字位数为 ‘1’ 的个数（也被称为 汉明重量).）。

提示：

• 请注意，在某些语言（如 Java）中，没有无符号整数类型。在这种情况下，输入和输出都将被指定为有符号整数类型，并且不应影响您的实现，因为无论整数是有符号的还是无符号的，其内部的二进制表示形式都是相同的。
• 在 Java 中，编译器使用 二进制补码 记法来表示有符号整数。因此，在上面的 示例 3 中，输入表示有符号整数 -3。

示例 1：

输入：n = 11 (控制台输入 00000000000000000000000000001011)
输出：3
解释：输入的二进制串 00000000000000000000000000001011 中，共有三位为 '1'。

示例 2：

输入：n = 128 (控制台输入 00000000000000000000000010000000)
输出：1
解释：输入的二进制串 00000000000000000000000010000000 中，共有一位为 '1'。

示例 3：

输入：n = 4294967293 (控制台输入 11111111111111111111111111111101，部分语言中 n = -3）
输出：31
解释：输入的二进制串 11111111111111111111111111111101 中，共有 31 位为 '1'。

提示：

• 输入必须是长度为 32 的 二进制串 。

题解：

• C++

class Solution {
public:
    int hammingWeight(uint32_t n) {
        int count = 0;
        while (n) {
            count++;
            n &= n - 1;// 去掉最后一个1
        }

        return count;
    }
};

• Golang

func hammingWeight(num uint32) int {
    count := 0

    for num > 0 {
        count++
        num &= num - 1
    }

    return count
}

（中等）剑指 Offer 16. 数值的整数次方

实现 pow(x, n)，即计算 x 的 n 次幂函数（即，xⁿ）。不得使用库函数，同时不需要考虑大数问题。

示例 1：

输入：x = 2.00000, n = 10
输出：1024.00000

示例 2：

输入：x = 2.10000, n = 3
输出：9.26100

示例 3：

输入：x = 2.00000, n = -2
输出：0.25000
解释：2-2 = 1/22 = 1/4 = 0.25

提示：

• -100.0 < x < 100.0
• -231 <= n <= 231-1
• -104 <= xn <= 104

题解：

• C++

class Solution {
public:
    double myPow(double x, int n) {
        double result = 1;
        long long nNew = n;

        if (nNew < 0) {
            x = 1 / x;
            nNew = -nNew;
        }

        while (nNew) {
            if (nNew & 1)
                result = result * x;
            x = x * x;
            nNew >>= 1;
        }
        
        return result;
    }
};

• Golang

func myPow(x float64, n int) float64 {
    r, nNew := float64(1), int64(n)

    if n < 0 {
        x = 1 / x
        nNew = -nNew
    }

    for nNew > 0 {
        if (nNew & 1) > 0 {
            r = r * x
        }

        x *= x
        nNew >>= 1
    }

    return r
}

---

（简单）剑指 Offer 17. 打印从1到最大的n位数

输入数字 n，按顺序打印出从 1 到最大的 n 位十进制数。比如输入 3，则打印出 1、2、3 一直到最大的 3 位数 999。

示例 1:

输入: n = 1
输出: [1,2,3,4,5,6,7,8,9]

说明：

• 用返回一个整数列表来代替打印
• n 为正整数

题解：

• C++

class Solution {
public:
    vector<int> printNumbers(int n) {
        int size = pow(10, n) - 1;
        vector<int> r(size, 0);

        int left = 1, right = size;

        while (left <= right) {
            r[left - 1] = left;
            r[right - 1] = right;
            left++;
            right--;
        }

        return r;
    }
};

• Golang

func printNumbers(n int) []int {
    size := int(math.Pow(10, float64(n)) - 1)

    r := make([]int, size)

    for i, j := 1, size; i <= j; i, j = i + 1, j - 1 {
        r[i - 1] = i
        r[j - 1] = j
    }

    return r
}

---

（简单）剑指 Offer 18. 删除链表的节点

给定单向链表的头指针和一个要删除的节点的值，定义一个函数删除该节点。

返回删除后的链表的头节点。

注意： 此题对比原题有改动

示例 1:

输入: head = [4,5,1,9], val = 5
输出: [4,1,9]
解释: 给定你链表中值为 5 的第二个节点，那么在调用了你的函数之后，该链表应变为 4 -> 1 -> 9.

示例 2:

输入: head = [4,5,1,9], val = 1
输出: [4,5,9]
解释: 给定你链表中值为 1 的第三个节点，那么在调用了你的函数之后，该链表应变为 4 -> 5 -> 9.

说明：

• 题目保证链表中节点的值互不相同
• 若使用 C 或 C++ 语言，你不需要 free 或 delete 被删除的节点

题解：

• C++

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* deleteNode(ListNode* head, int val) {
        if (!head) {
            return nullptr;
        }

        if (head->val == val) {
            return head->next;
        }

        ListNode* pre = head, *cur = head->next;

        while (cur) {
            if (cur->val == val) {
                pre->next = cur->next;
                break;
            }

            pre = cur;
            cur = cur->next;
        }

        return head;
    }
};

• Golang

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func deleteNode(head *ListNode, val int) *ListNode {
    if head == nil {
        return nil
    }
    
    if head.Val == val {
        return head.Next
    }
    pre, cur := head, head.Next
    for head != nil {
        if cur.Val == val {
            pre.Next = cur.Next
            break
        }

        pre = cur
        cur = cur.Next
    }

    return head
}

---

（困难）剑指 Offer 19. 正则表达式匹配

请实现一个函数用来匹配包含'. '和'*'的正则表达式。模式中的字符'.'表示任意一个字符，而'*'表示它前面的字符可以出现任意次（含0次）。在本题中，匹配是指字符串的所有字符匹配整个模式。例如，字符串"aaa"与模式"a.a"和"ab*ac*a"匹配，但与"aa.a"和"ab*a"均不匹配。

示例 1:

输入:
s = "aa"
p = "a"
输出: false
解释: "a" 无法匹配 "aa" 整个字符串。

示例 2:

输入:
s = "aa"
p = "a*"
输出: true
解释: 因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。

示例 3:

输入:
s = "ab"
p = ".*"
输出: true
解释: ".*" 表示可匹配零个或多个（'*'）任意字符（'.'）。

示例 4:

输入:
s = "aab"
p = "c*a*b"
输出: true
解释: 因为 '*' 表示零个或多个，这里 'c' 为 0 个, 'a' 被重复一次。因此可以匹配字符串 "aab"。

示例 5:

输入:
s = "mississippi"
p = "mis*is*p*."
输出: false

提示：

• s 可能为空，且只包含从 a-z 的小写字母。
• p 可能为空，且只包含从 a-z 的小写字母以及字符 . 和 *，无连续的 '*'。

题解：

• C++

class Solution {
public:
    bool isMatch(string s, string p) {
        int m = s.size();
        int n = p.size();
        // lambda 表达式：s 和 p 通过引用传递
        // s 要匹配的第 i 个，下标 i - 1
        // p 要匹配的第 j 个，下表 j - 1
        auto matches = [&s, &p](int i, int j) {
            if (i == 0) {
                return false;
            }

            if (p[j - 1] == '.') {
                return true;
            }

            return (s[i - 1] == p[j - 1]);
        };

        vector<vector<int>> f(m + 1, vector<int>(n + 1));
        // i = 0, j = 0 表示 s 和 p 都没有字符
        f[0][0] = true;
        for (int i = 0; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (p[j - 1] == '*') {
                    f[i][j] |= f[i][j - 2]; // 匹配 0 个 * 前面的字符
                    if (matches(i , j - 1)) { // 
                        f[i][j] |= f[i - 1][j];
                    }
                } else {
                    if (matches(i, j)) {
                        f[i][j] |= f[i - 1][j - 1];
                    }
                }
            }
        }

        return f[m][n];
    }
};

• Golang

func isMatch(s string, p string) bool {
    m, n := len(s), len(p)

    matches := func(i, j int) bool {
        if i ==0 {
            return false
        }

        if p[j - 1] == '.' {
            return true
        }

        return s[i - 1] == p[j - 1]
    }

    f := make([][]bool, m + 1)
    for index := 0; index < len(f); index++ {
        f[index] = make([]bool, n + 1)
    }

    f[0][0] = true

    for i := 0; i <= m; i++ {
        for j := 1; j <= n; j++ {
            if p[j - 1] == '*' {
                f[i][j] = f[i][j] || f[i][j - 2]
                if matches(i , j - 1) {
                    f[i][j] = f[i][j] || f[i - 1][j]
                }
            } else {
                if matches(i, j) {
                    f[i][j] = f[i][j] || f[i - 1][j - 1]
                }
            }
        }
    }

    return f[m][n]
}

---

题解：

• C++

• Golang