第九、十讲 复杂DP+疑难杂题
文章目录
- 复杂DP
-
- 鸣人的影分身(DP/DFS)
- 糖果(dp/01背包)
- 密码脱落(区间dp)
- 包子凑数(完全背包,数论结论)
- 括号配对(dp、典型区间dp)
- 石子合并(区间DP)
- 疑难杂题
-
- 修改数组(并查集)
- 倍数问题
只选取了部分感觉比较有代表性的
复杂DP
鸣人的影分身(DP/DFS)
法1:DP
题意就是给你M能量分为N份,有的份可以为0,共有多少种方案。
我们设dp[i][j]表示共能量I分给j个分身的方案数。
我们可以由两种状态转换过来
(1)有一个人能量值为0,(相当于少了一个分身,但是我们的能量值并没有变)dp[i][j-1]
(2)所有人能量值都不为0,(那就首先先给所有人都分1能量值,在将剩下的i-j分给j个人,可以保证每个分身能量值都不为0)dp[i-j][j]
由此我们得到状态转移方程为:
(✍给自己理解的:需要注意的是并不是只有一个人能量值为0,只是在当前状态下有一个人为0,在递推过程中不只是仅仅1个人能量值为0)
dp[i][j]=dp[i][j-1]+dp[i-j][j]
当i 法2:dfs 初始化: 思路: 初始化 法1:暴力,显然会TLE 法2:并查集import java.io.PrintWriter;
import java.util.Arrays;
import java.util.Scanner;
public class Main{
static Scanner sc = new Scanner(System.in);
static int[][]dp = new int[20][20];
public static void main(String[] args) throws Exception{
int t = sc.nextInt();
while(t-- > 0) {
int ans = 0;
int m = sc.nextInt();//能量值
int n = sc.nextInt();//个数
dp[0][0] = 1;
for(int i = 0;i <= m; i++) {//
for(int j = 1; j <= n; j++) {
dp[i][j] = dp[i][j - 1];//有一个分身为0
if(i >= j) {//能量值大于分身个数
dp[i][j] += dp[i-j][j];
}
}
}
System.out.println(dp[m][n]);
}
}
}
import java.io.PrintWriter;
import java.util.Arrays;
import java.util.Scanner;
public class Main{
static Scanner sc = new Scanner(System.in);
static int n = 0,m = 0,ans = 0;
public static void main(String[] args) throws Exception{
int t = sc.nextInt();
while(t-- > 0) {
m = sc.nextInt();//能量值
n = sc.nextInt();//个数
ans = 0;
dfs(m,0,0);
System.out.println(ans);
}
}
private static void dfs(int cur, int num, int next) {
//cur代表当前能量值,num代表当前分身个数,next代表下次分配的能量值
if(num == n) {//当前分身个数为n
if(cur == 0) {//能量值全部分完
ans++;
}
return;//注意return的位置
}
for(int i = next; i <= cur; i++) {
dfs(cur-i,num+1,i);
}
}
}
糖果(dp/01背包)


显然N是dp状态的其中一维,但是可以凑出来糖果数量肯定是不能作为dp的维度的,太大啦…
我们设dp[o][j]表示前i个物品,总价值%k=j的最大值
我们需要求的是最大值
转移方程:
(1)选第i个:dp[i][j]=dp[i-1][j-w%k]+w
因为选了第i个为dp[i][j[那么假设没选之前是S,
(S+a[i])%k=j->s%k+a[i]%k=j
所以可以得到s%k=j-a[i]%k
(2)不选第i个产品f[i - 1][j]
注意点:
(1)转移方程中的(j−w[i])%k)(j−w[i])%k)可能为负的,必须要将余数变成[0,n−1][0,n−1]之间,要变成(j−w[i])%k+k)%k
dp[0][i]是没有意义的,初始化为-inf,❓import java.util.Scanner;
public class Main{
static Scanner sc = new Scanner(System.in);
static int n = 0,m = 0,ans = 0;
static int[][]dp = new int[110][110];
public static void main(String[] args) throws Exception{
n = sc.nextInt();
m = sc.nextInt();
for(int i = 0; i < 110; i++) {
dp[0][i] = -0x3f3f3f3f;//注意必须初始化为-Inf
}
dp[0][0] = 0;
for(int i = 1; i <= n; i++) {
int w = sc.nextInt();
for(int j = 0; j < m; j++) {
dp[i][j] = dp[i - 1][j]; //不选
dp[i][j] = Math.max(dp[i][j], dp[i - 1][(j - w % m + m ) % m] + w);
}
}
System.out.println(dp[n][0]);//mod为0代表可以整除
}
}
密码脱落(区间dp)

dp[i][j]为字符串[i,j]至少脱落数
状态转移:
(1)当str[i]==str[j]时缩短字符串
(2)如果不相等,取在左边补一个和右边一样的字符串和在右边补一个和左边一样的字符串的最小值
初始化:
当就1个字符的时候,肯定是对称的#include 包子凑数(完全背包,数论结论)
我们有一个结论(裴蜀定理):任意两个数的组合必定是他们gcd的任意两个数的组合必定是他们gcd的 倍数
如果两个数的gcd不是1,那么他们有无数个不可以凑出来的数
当gcd为1的时候,不能凑出来的最大数是:(a-1)*(b-1)-1,所以我们的枚举上限变为10000((99-1)(98-1))
此时这个问题就可以使用完全背包进行求解了
1.状态:
dp[i][j]前i个物品,能否凑出重量为j
2.状态转移: dp[i][j] = dp[i-1][j];
dp[i][j] = max(dp[i][j], max(dp[i-1][j-w[i]]+v[i], dp[i][j-w[i]]+v[i]));( j >= w[i])
//背包容量放的下
import java.util.Scanner;
public class Main{
static Scanner sc = new Scanner(System.in);
static int n = 0,m = 0,ans = 0;
static boolean[][]dp = new boolean[110][11000];
static int[] w = new int[110];
public static void main(String[] args) throws Exception{
n = sc.nextInt();
int d = 0;
for(int i = 1; i <= n; i++) {
w[i] = sc.nextInt();
d = gcd(d,w[i]);
}
if(d != 1) {
System.out.println("INF");
}else {
int maxn = 10000;
dp[0][0] = true;
for(int i = 1; i <= n; i++) {
for(int j = 0; j < maxn; j++) {
dp[i][j] = dp[i - 1][j]; //这一层不选
if(j >= w[i]) {
dp[i][j] |= (dp[i][j - w[i]]|dp[i-1][j-w[i]]);
}
}
}
for(int i = 0; i < maxn; i++) {
if(!dp[n][i]) {
ans++;
}
}
System.out.println(ans);
}
}
private static int gcd(int a, int b) {
if(b == 0) return a;
return gcd(b,a%b);
}
}
括号配对(dp、典型区间dp)


回归到本题:
定义
dp[i][j]表示字符串[i,j]需要添加的最少字符串
状态转移:
(1)如果si与sj匹配,那么直接由(i+1,j-1转移过来):dp[i][j]=dp[i+1][j-1]
(2)如果si与sj不匹配的话,我们需要枚举分割点,(❗这道题和上面的密码脱落不太一样,上面的密码脱落不匹配的话直接由 dp[i][j-1], dp[i+1][j]其中之一转移,由于那道题要求对称,但是本题,首尾不相同的话可能由这种情况,明显是不需要进行添加的
此时我们需要在起点和终点之间枚举分割点:取最小值即可dp(i,j)=min(dp(i,j),dp(i,k)+dp(k+1,j))(i<=k<=j)
初始化长度为1的时候,dp[][]=1;因为就一个,肯定需要补一个,因为本题需要取最小值,所以其他情况初始化为infimport java.util.Scanner;
public class Main{
static Scanner sc = new Scanner(System.in);
static int[][]dp = new int[110][110];
static int n = 0,m = 0,ans = 0;
static int Inf = 0x3f3f3f3f;
static int[] w = new int[110];
static String str = "";
public static void main(String[] args) throws Exception{
str = sc.nextLine();
for(int i = 0; i < str.length(); i++) {
dp[i][i] = 1;
}
for(int len = 2; len <= str.length(); len++) {
for(int l = 0; l + len - 1 < str.length(); l++) {
int r = l + len - 1;
dp[l][r] = Inf;
if(check(l,r)) {
dp[l][r] = Math.min(dp[l][r],dp[l+1][r-1]);
}
for (int k = l; k <= r; k++) {
dp[l][r] = Math.min(dp[l][r], dp[l][k] + dp[k + 1][r]);
}
}
}
System.out.println(dp[0][str.length() - 1]);
}
private static boolean check(int l, int r) {
if (str.charAt(l) == '[' && str.charAt(r) == ']' || str.charAt(l) == '(' && str.charAt(r) ==')') {
return true;
}
return false;
}
}
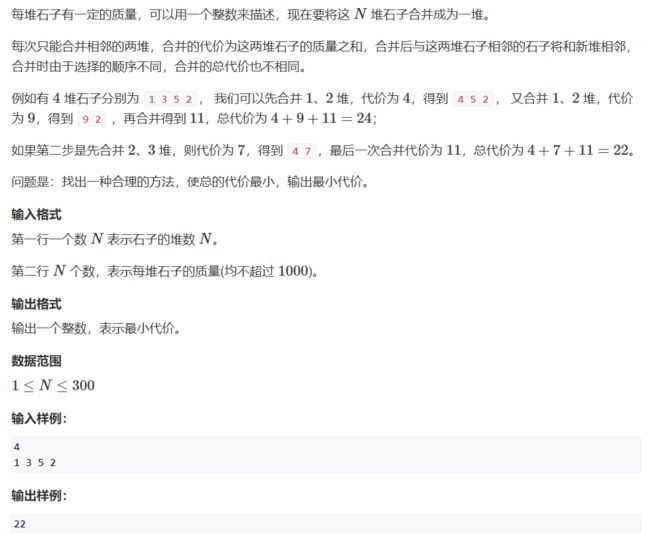
石子合并(区间DP)
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.util.Arrays;
public class Main {
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
static int N = 310;
static int[]a = new int[N];
static int[]s = new int[N];
static int [][]f = new int[N][N];
static int INF = 0x3f3f3f3f;
static int n = 0;
public static void main(String[] args) throws Exception{
init();
n = Integer.parseInt(br.readLine());
String aa[] = br.readLine().split(" ");
for(int i = 1; i <= n; i++) {
a[i] = Integer.parseInt(aa[i - 1]);
s[i] = s[i - 1] +a[i];
f[i][i] = 0;
}
for(int len = 2; len <= n; len++) {
for(int l = 1; l + len - 1 <= n; l++) {
int r = l + len - 1;
for(int k = 1; k < r; k++) {
f[l][r] = Math.min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
}
}
}
System.out.println(f[1][n]);
}
private static void init() {
for(int i = 0; i < N; i++) {
for(int j = 0; j < N; j++) {
f[i][j] = INF;
}
}
}
}
疑难杂题
修改数组(并查集)
import java.util.Scanner;
public class Main{
static Scanner sc = new Scanner(System.in);
static int N = (int) (1e6 + 10);
static boolean[] vis = new boolean[N];
static int[]a = new int[N];
static String str = "";
static int n = 0;
public static void main(String[] args) throws Exception{
n = sc.nextInt();
for(int i = 1; i <= n; i++) {
a[i] = sc.nextInt();
}
for(int i = 1; i <= n; i++) {
if(!vis[a[i]]) {
vis[a[i]] = true;
}else {
while(vis[a[i]]) a[i]++;
vis[a[i]] = true;
}
}
for(int i = 1; i <= n; i++) {
System.out.print(a[i] + " ");
}
}
}
import java.util.Scanner;
public class Main{
static int N = (int)(1e6 + 10);
static int[] p = new int[N];
static int find(int x) //利用路径压缩进行优化
{
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
for(int i = 0;i <= 1000000;i ++) p[i] = i;
for(int i = 0;i < n;i ++)
{
int x = scan.nextInt();
x = find(x);
System.out.print(x + " ");
p[x] = x + 1; //每次指向下一个元素的位置
}
}
}
//比如1 2 3 4 5每个人都指向自己
//来了一个2,此时寻找2的父节点,2输出,并将其父节点设为3
//又来了一个1,寻找其父节点1,输出,并将其指向2
//此时又来一个1,查找其父节点,1!=f[1],find(2)=f[2]=3,所以此时为3,并将其父节点设为4
//来了一个3,查找父亲,为4,并将父节点设为5
//来了个4,输出父节点5
倍数问题