一本通 3.3.1 树与二叉树
树与二叉树的基本知识
1336:【例3-1】找树根和孩子
【题目描述】
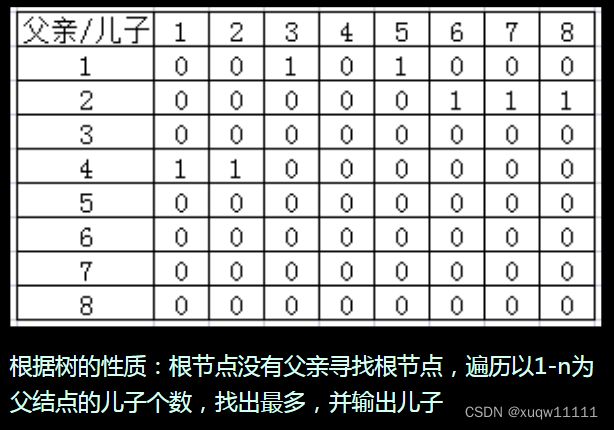
给定一棵树,输出树的根root,孩子最多的结点max以及他的孩子。
【题目分析】
【代码实现】
#include
using namespace std;
int father[201], sum[101];
/*前提是父亲的孩子不能相同*/
int main() {
int m, n;
cin >> n >> m;
for (int i = 1; i <= m; i++) {
int x, y;
cin >> x >> y;
father[y] = x;
sum[x]++;
}
int root = 0;
for (int i = 1; i <= n; i++) {
if (father[i] == 0) {
root = i;
break;
}
}
int maxn = 0, maxjie = 0;
for (int i = 1; i <= n; i++) {
if (maxn < sum[i]) {
maxn = sum[i];
maxjie = i;
}
}
cout << root << endl << maxjie << endl;
for (int i = 1; i <= n; i++) {
if (father[i] == maxjie) {
cout << i << " ";
}
}
} 1337:【例3-2】单词查找树
【题目描述】
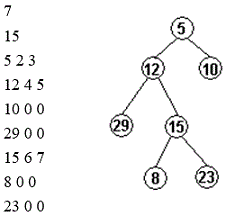
在进行文法分析的时候,通常需要检测一个单词是否在我们的单词列表里。为了提高查找和定位的速度,通常都画出与单词列表所对应的单词查找树,其特点如下:
1.根结点不包含字母,除根结点外每一个结点都仅包含一个大写英文字母;
2.从根结点到某一结点,路径上经过的字母依次连起来所构成的字母序列,称为该结点对应的单词。单词列表中的每个单词,都是该单词查找树某个结点所对应的单词;
3.在满足上述条件下,该单词查找树的结点数最少。
4.例如图3-2左边的单词列表就对应于右边的单词查找树。注意,对一个确定的单词列表,请统计对应的单词查找树的结点数(包含根结点)。
【题目分析】
将所有单词进行字典顺序排序,依次计算每个单词对前一个单词的差,并把差累加起来;第一个单词相对于“空”的差为该单词的长度,累加和再加上1(根节点),输出结果
特别的:读取单词时会将最后一个空字符串读入,排序时注意开始下标和结束下标
【代码实现】
#include
using namespace std;
string s[4000];
int main() {
//input data
int n = 0;
while (cin >> s[++n]) ;
// n--;
sort(s + 1, s + n + 1);
int ans = s[1].length();
for (int i = 2; i <= n; i++) {
int len = min(s[i - 1].length(), s[i].length());
int j = 0;
while (j < len) {
if (s[i - 1][j] == s[i][j]) j++;
else break;
}
ans += (s[i].length() - j);
}
cout << ans + 1 << endl;
return 0;
} 1338:【例3-3】医院设置
【题目描述】
设有一棵二叉树(如下图),其中圈中的数字表示结点中居民的人口,圈边上数字表示结点编号。现在要求在某个结点上建立一个医院,使所有居民所走的路程之和为最小,同时约定,相邻结点之间的距离为11。就本图而言,若医院建在11处,则距离和=4+12+2×20+2×40=136;若医院建在3处,则距离和=4×2+13+20+40=81……
【题目分析】
树的中心点问题
方法1:枚举,使用floyed求解每两个节点之间的距离,枚举每个节点计算其他节点权值乘以到该点距离的最小值
方法2:深搜,使用深搜求解每个节点到其他节点的距离乘以权值,寻找最小值即可
【代码实现】
方法1 枚举
#include
using namespace std;
const int INF = 0x3f3f3f3f;
int g[101][101];
int a[101];
int main() {
int n;
cin >> n;
memset(g, 0x3f, sizeof(g)); //最为无穷大
for (int i = 1; i <= n; i++) { //读入距离
int l, r;
g[i][i] = 0;
cin >> a[i] >> l >> r;
if (l > 0)g[i][l] = g[l][i] = 1;
if (r > 0)g[i][r] = g[r][i] = 1;
}
//floyed算法求任意两点之间的距离
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
g[i][j] = min(g[i][j], g[i][k] + g[k][j]);
}
}
}
//枚举求最小值
int ans = INF;
for (int i = 1; i <= n; i++) {
int sum = 0;
for (int j = 1; j <= n; j++) {
sum += a[j] * g[i][j];
}
ans = min(ans, sum);
}
//输出结果
cout << ans << endl;
return 0;
} 方法2 深搜
#include
using namespace std;
struct node {
int data, father, left, right;
} a[10001];
int n, ans = INT_MAX, v[10001] = {0};
int f(int x, int d) {
if (x == 0 || v[x] == 1)
return 0;
v[x] = 1;
int l = f(a[x].left, d + 1);
int r = f(a[x].right, d + 1);
int t = f(a[x].father, d + 1);
return l + r + t + a[x].data * d;
}
int main() {
cin >> n;
for (int i = 1; i <= n; i++)
cin >> a[i].data >> a[i].left >> a[i].right;
for (int i = 1; i <= n; i++) {
a[a[i].left].father = i;
a[a[i].right].father = i;
}
for (int i = 1; i <= n; i++) {
memset(v, 0, sizeof(v));
ans = min(f(i, 0), ans);
}
cout << ans << endl;
return 0;
} 1339:【例3-4】求后序遍历
【题目描述】
输入一棵二叉树的先序和中序遍历序列,输出其后序遍历序列。
【题目分析】
根据先序的第一个字符,将中序划分为左子树和右子树,长度为Ln的左子树字符串和先序后Ln长度的字符串递归划分,长度为Rn的右子树字符串和先序倒数Rn长度的字符串递归划分,最后输出当前的字符。
【代码实现】
#include
using namespace std;
void calc(string s1, string s2) {
int m = s2.find(s1[0]); //m是字符s1[0]在字符串s2中的下标 位置为 m+1
int l1 = s1.length(); //s1的字符个数
int l2 = s2.length(); //s2的字符个数
if (m > 0)
calc(s1.substr(1, m), s2.substr(0, m)); //递归左子树
if (m < l2-1)
calc(s1.substr(m + 1, l1 - (m + 1)), s2.substr(m + 1, l2 - (m + 1))); //递归右子树
cout<> s1 >> s2;
calc(s1, s2);
cout << endl;
//clock_t s = clock();
//cout < 1340:【例3-5】扩展二叉树
【题目描述】
由于先序、中序和后序序列中的任一个都不能唯一确定一棵二叉树,所以对二叉树做如下处理,将二叉树的空结点用·补齐,如图所示。我们把这样处理后的二叉树称为原二叉树的扩展二叉树,扩展二叉树的先序和后序序列能唯一确定其二叉树。
现给出扩展二叉树的先序序列,要求输出其中序和后序序列。
【题目分析】
使用链式结构递归建立二叉树,如果当前字符不为'.',当前节点值域为该字符,递归建立左子树和右子树,否则当前节点为NULL
递归输出中序序列,如果当前节点不为NULL,遍历左子树,输出当前节点值域,遍历右子树
递归输出后续序列,如果当前节点不为NULL,遍历左子树,遍历右子树,输出当前节点值域
【代码实现】
#include
using namespace std;
struct node;
typedef node* tree;
struct node {
char data;
tree lchild;
tree rchild;
};
tree bt;
string s;
int i = -1;
void build(tree &bt) {
if(s[++i]!='.'){
bt=new node;
bt->data=s[i];
build(bt->lchild);
build(bt->rchild);
}
else{
bt=NULL;
}
}
void print2(tree bt){
if(bt!=NULL){
print2(bt->lchild);
cout<data;
print2(bt->rchild);
}
}
void print3(tree bt){
if(bt!=NULL){
print3(bt->lchild);
print3(bt->rchild);
cout<data;
}
}
int main() {
//input data
cin >> s;
i = -1;
build(bt);
print2(bt);
cout< 1363:小球(drop)
【题目描述】
许多的小球一个一个的从一棵满二叉树上掉下来组成FBT(Full Binary Tree,满二叉树),每一时间,一个正在下降的球第一个访问的是非叶子节点。然后继续下降时,或者走右子树,或者走左子树,直到访问到叶子节点。决定球运动方向的是每个节点的布尔值。最初,所有的节点都是false,当访问到一个节点时,如果这个节点是false,则这个球把它变成true,然后从左子树走,继续它的旅程。如果节点是true,则球也会改变它为false,而接下来从右子树走。满二叉树的标记方法如下图:
因为所有的节点最初为false,所以第一个球将会访问节点1,节点2和节点4,转变节点的布尔值后在在节点8停止。第二个球将会访问节点1、3、6,在节点12停止。明显地,第三个球在它停止之前,会访问节点1、2、5,在节点10停止。
现在你的任务是,给定FBT的深度D,和I,表示第I个小球下落,你可以假定I不超过给定的FBT的叶子数,写一个程序求小球停止时的叶子序号。
【题目分析】
使用一维数组存储该满二叉树,根据完全二叉树的性质根节点为i,右儿子为2*i,左儿子为2*i+1进行模拟
【代码实现】
使用数组存储结构
#include
using namespace std;
const int maxn = 1050000;
bool data[maxn];
int n, m;
int main() {
//input data
cin >> n >> m;
int _count = (int)pow(2, n) - 1;
//clock_t s = clock();
int index = 0;
for (int i = 1; i <= m; i++) {
int j = 1;
while (j * 2 <= _count) {
if (data[j]) {
data[j] = false;
j = j * 2 + 1;
} else {
data[j] = true;
j = j * 2;
}
}
index = j;
}
cout << index;
//cout < 使用链表存储结构
#include
using namespace std;
struct node;
typedef node* tree;
const int maxn = 1050000;
struct node {
bool data;
int index;
tree lchild;
tree rchild;
} nodes[maxn];
int n, m;
int mn;
int main() {
//input data
cin >> n >> m;
//build BT
mn = (int)pow(2, n) - 1;
for (int i = 1; i <= mn; i++) {
if (2 * i <= mn)
nodes[i].lchild = &nodes[i * 2];
if (2 * i + 1 <= mn)
nodes[i].rchild = &nodes[i * 2 + 1];
nodes[i].data = false;
nodes[i].index = i;
}
//simulated processing
tree bt;
for (int i = 1; i <= m; i++) {
bt = &nodes[1];
while (bt->lchild != NULL) {
if (bt->data) {
bt->data = false;
bt = bt->rchild;
} else {
bt->data = true;
bt = bt->lchild;
}
}
}
cout << bt->index;
//clock_t s = clock();
//cout < 1364:二叉树遍历(flist)
【题目描述】
树和二叉树基本上都有先序、中序、后序、按层遍历等遍历顺序,给定中序和其它一种遍历的序列就可以确定一棵二叉树的结构。
假定一棵二叉树一个结点用一个字符描述,现在给出中序和按层遍历的字符串,求该树的先序遍历字符串。
【题目分析】
问题本质:已知层序和中序求前序序列
层序遍历中第1个字符是该树的根,首先输出,使用该字符将中序序列一分为二,左侧为左子树ls1,右侧为右子树rs1,按照层序序列的顺序将左子树中出项的字符截取出来ls2,将右子树中出项的字符截取出来rs2,当两者不为空时,递归解决(ls1,ls2) (rs1,rs2)
【代码实现】
#include
using namespace std;
void printPre(string s1, string s2) {
int l1 = s1.length();
int l2 = s2.length();
int m = s1.find(s2[0]);
string ls1 = s1.substr(0, m);
string rs1 = s1.substr(m + 1, l1 - (m + 1));
string ls2 = "";
string rs2 = "";
for (int i = 1; i < l2; i++) {
if (ls1.find(s2[i]) != string::npos) {
ls2 += s2[i];
}
if (rs1.find(s2[i]) != string::npos) {
rs2 += s2[i];
}
}
cout << s1[m];
if (m > 0)
printPre(ls1, ls2);
if (m < l1 - 1)
printPre(rs1, rs2);
}
int main() {
//input data
string s1, s2;
cin >> s1 >> s2;
printPre(s1, s2);
cout << endl;
//clock_t s = clock();
//cout < 1365:FBI树(fbi)
【题目描述】
我们可以把由“00”和“11”组成的字符串分为三类:全“00”串称为B串,全“1”串称为I串,既含“0”又含“1”的串则称为F串。
FBI树是一种二叉树,它的结点类型也包括F结点,B结点和I结点三种。由一个长度为2N的“01”串S可以构造出一棵FBI树T,递归的构造方法如下:
T的根结点为R,其类型与串S的类型相同;
若串S的长度大于1,将串S从中间分开,分为等长的左右子串S1和S2;由左子串S1构造R的左子树T1,由右子串S2构造R的右子树T2。
现在给定一个长度为2N的“01”串,请用上述构造方法构造出一棵FBI树,并输出它的后序遍历序列。
【题目分析】
问题的解决:对于后序遍历来说,是先输出左子树,再输出右子树,最后是根节点
递归求解类似于二分求解问题,根据左右子树的情况合并问题解,基线条件为一个0/1容易判断
【代码实现】
单个数组存储数据
#include
using namespace std;
char nodes[2050];
int n;
void build(string s, int cur) {
if (cur <= n) {
//set current node
int n0 = 0, n1 = 0;
for (int i = 0; i < (int)s.length(); i++) {
if (s[i] == '0') n0++;
if (s[i] == '1') n1++;
if (n0 > 0 && n1 > 0) break;
}
if (n0 == 0 && n1 > 0) nodes[cur] = 'I';
if (n0 > 0 && n1 == 0) nodes[cur] = 'B';
if (n0 > 0 && n1 > 0) nodes[cur] = 'F';
int len = s.length();
build(s.substr(0, len / 2), cur * 2);
build(s.substr(len / 2, len / 2), cur * 2 + 1);
cout << nodes[cur];
}
}
int main() {
//input data
string s;
cin >> n >> s;
n = pow(2, n + 1) - 1;
build(s, 1);
cout << endl;
//clock_t s = clock();
//cout < 多个数组存储数据
#include
using namespace std;
char data[2050];
int lchild[2050];
int rchild[2050];
int n;
int _count = 1;
void build(string s, int cur) {
int len = s.length();
if (len > 1) {
lchild[cur] = ++_count;
build(s.substr(0, len / 2), lchild[cur]);
rchild[cur] = ++_count;
build(s.substr(len / 2, len / 2), rchild[cur]);
if (data[lchild[cur]] != data[rchild[cur]] )
data[cur] = 'F';
else if (data[lchild[cur]] == 'F')
data[cur] = 'F';
else if (data[lchild[cur]] == 'B')
data[cur] = 'B';
else
data[cur] = 'I';
} else {
if (s[0] == '0')
data[cur] = 'B';
if (s[0] == '1')
data[cur] = 'I';
}
cout<> n >> s;
n = pow(2, n + 1) - 1;
cout<<"Post-order:";
build(s, 1);
cout< 链表结构存储
#include
using namespace std;
struct node;
typedef node* tree;
struct node {
char data;
tree lchild;
tree rchild;
};
void build(string s, tree &bt) {
int len = s.length();
bt = new node;
if (len > 1) {
build(s.substr(0, len / 2), bt->lchild);
build(s.substr(len / 2, len / 2), bt->rchild);
if (bt->lchild->data != bt->rchild->data)
bt->data = 'F';
else if (bt->lchild->data == 'F')
bt->data = 'F';
else if (bt->lchild->data == 'B')
bt->data = 'B';
else
bt->data = 'I';
} else {
if (s[0] == '0')
bt->data = 'B';
if (s[0] == '1')
bt->data = 'I';
}
cout<data;
}
int main() {
//input data
int n;
string s;
tree bt;
cin >> n >> s;
build(s, bt);
//clock_t s = clock();
//cout < 1366:二叉树输出(btout)
【题目描述】
树的凹入表示法主要用于树的屏幕或打印输出,其表示的基本思想是兄弟间等长,一个结点的长度要不小于其子结点的长度。二叉树也可以这样表示,假设叶结点的长度为1,一个非叶结点的长度等于它的左右子树的长度之和。
一棵二叉树的一个结点用一个字母表示(无重复),输出时从根结点开始:
每行输出若干个结点字符(相同字符的个数等于该结点长度),
如果该结点有左子树就递归输出左子树;
如果该结点有右子树就递归输出右子树。
假定一棵二叉树一个结点用一个字符描述,现在给出先序和中序遍历的字符串,用树的凹入表示法输出该二叉树。
【题目分析】
问题的解决:字母输出顺序为先序顺序,定义统计个数数组a[i], 先序序列为s1,中序序列为s2,查找s1的第1个字符在s2位置m,如果m>0,说明可以递归求解左子树节点个数 s1 从1开始取m个字符,s2从0开始取m个字符,否则左子树节点个数为0,如果m 已知一棵二叉树用邻接表结构存储,中序查找二叉树中值为x的结点,并指出是第几个结点。例:如图二叉树的数据文件的数据格式如下: 可以使用数组进行数据的存储 val存储节点的数据,lchild存储左孩子的编号,rchild存储右孩子的编号,使用中序遍历(先查询左孩子,再查询根节点,最后查询右孩子,每查询一次根节点 计数cnt++,判断当前节点值是否与中值相等),最后输出中值相等的计数 如果二叉树的左右子树的结构是对称的,即两棵子树皆为空,或者皆不空,则称该二叉树是对称的。编程判断给定的二叉树是否对称. 例:如下图中的二叉树T1是对称的,T2是不对称的。 二叉树用顺序结构给出,若读到#则为空,二叉树T1=ABCDE,T2=ABCD#E,如果二叉树是对称的,输出“Yes”,反之输出“No”。 通过规律去总结,从字符串的第二个字符开始每两个取一组,如果中间有一个字母和一个'#',该bt不为对称树,:经过上面的判断后,还有一种特殊情况,字符串长度为偶数,说明最后省略了一个字符,有一个单只子树,也不是对称树。【代码实现】
#include 1367:查找二叉树(tree_a)
【题目描述】
【题目分析】
【代码实现】
#include 1368:对称二叉树(tree_c)
【题目描述】
【题目分析】
【代码实现】
#include