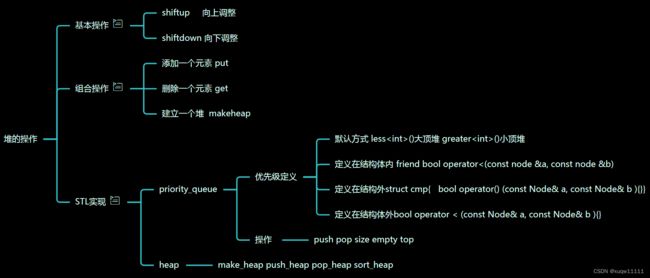
一本通 3.3.2 堆和优先队列的基本应用

堆和优先队列的基本应用

1369：合并果子(fruit)

【题目描述】

在一个果园里，多多已经将所有的果子打了下来，而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。

每一次合并，多多可以把两堆果子合并到一起，消耗的体力等于两堆果子的重量之和。可以看出，所有的果子经过n−1次合并之后，就只剩下一堆了。多多在合并果子时总共消耗的体力等于每次合并所耗体力之和。

因为还要花大力气把这些果子搬回家，所以多多在合并果子时要尽可能地节省体力。假定每个果子重量都为11，并且已知果子的种类数和每种果子的数目，你的任务是设计出合并的次序方案，使多多耗费的体力最少，并输出这个最小的体力耗费值。

例如有33种果子，数目依次为1，2，9。可以先将 1、2堆合并，新堆数目为3，耗费体力为3。接着，将新堆与原先的第三堆合并，又得到新的堆，数目为12，耗费体力为 12。所以多多总共耗费体力=3+12=15。可以证明15为最小的体力耗费值。

【题目分析】

  贪心算法 果子从小到大排序，计算前缀和，再将所有数值相加。

【代码实现】

#include 

using namespace std;

vector h;

int main() {
	//input data
	int n;
	cin >> n;
	for (int i = 1; i <= n; i++) {
		int x;
		cin >> x;
		h.push_back(x);
	}

	make_heap(h.begin(), h.end(), greater()); //small heap

	int ans = 0;
	for (int i = 1; i <= n - 1; i++) {
		pop_heap(h.begin(), h.end(), greater());
		int s1 = h.back();
		h.pop_back();
		pop_heap(h.begin(), h.end(), greater());
		int s2 = h.back();
		h.pop_back();
		h.push_back(s1 + s2);
		push_heap(h.begin(), h.end(), greater());
		ans += s1 + s2;
	}
	cout << ans;
	return 0;
}

1370：最小函数值(minval)

【题目描述】

有n个函数，分别为F1,F2,...,Fn。定义Fi(x)=Aix2+Bix+Ci(x∈N∗)。给定这些Ai、Bi和Ci，请求出所有函数的所有函数值中最小的m个（如有重复的要输出多个）。

【题目分析】

函数为一元二次函数，且所有系数都是大于0的正整数，在1-m区间内函数都是单调递增的。

使用第一个函数产生m个函数值放入堆中，后面的函数产生的函数值如果小于堆的最大值，移除堆顶元素 压入新函数值，否则计算下一个函数。

【代码实现】

#include 

using namespace std;


priority_queue value;  //大顶堆

int main() {
	//input data

	int n, m;

	cin >> n >> m;
	int a, b, c;
	cin >> a >> b >> c;
	for (int i = 1; i <= m; i++) {              //使用第1个函数，先算m个数，加满队列
		int v = (a * i + b) * i + c;
		value.push(v);
	}
	for (int i = 2; i <= n; i++) {
		cin >> a >> b >> c;
		int j = 1;
		while (true) {
			int v = (a * j + b) * j + c;
			if (v < value.top()) {
				value.pop();
				value.push(v);
			}
			else
				break;
			j++;
		}

	}

	int ans[10005];
	for (int i = 1; i <= m; i++) {
		ans[i] = value.top();
		value.pop();
	}
	for (int i = m; i >= 1; i--) {
		cout << ans[i] << " ";
	}
	return 0;
}

1371：看病

【题目描述】

有个朋友在医院工作，想请BSNY帮忙做个登记系统。具体是这样的，最近来医院看病的人越来越多了，因此很多人要排队，只有当空闲时放一批病人看病。但医院的排队不同其他排队，因为多数情况下，需要病情严重的人优先看病，所以希望BSNY设计系统时，以病情的严重情况作为优先级，判断接下来谁可以去看病。

【题目分析】

维护一个大顶堆，查询时如果堆为空输出none，否则输出堆顶元素，
插入操作：将数据放入堆的最后，向上调整  时间复杂度为log(n)。
删除操作：取出堆顶元素，将最后一个元素移到堆顶，向下调整  时间复杂度为log(n)。

【代码实现】

#include 

using namespace std;
struct node {
	char  name[25];
	int priority;
	friend bool operator<(const node &a, const node &b) {
		return a.priority < b.priority;
	}
};
priority_queue  p;

int main() {
	//input data
	int n;
	cin >> n;
	char inchar[105];
	char pop[] = "pop";
	node a;
	for (int i = 1; i <= n; i++) {
		scanf("%s", inchar);
		if (strcmp(inchar, pop) == 0) {
			if (p.empty()) printf("none\n");
			else {
				printf("%s %d\n", p.top().name, p.top().priority);
				p.pop();
			}
		} else {
			scanf("%s%d", a.name, &a.priority);
			p.push(a);
		}
	}
	return 0;
}

1372：小明的账单

【题目描述】

小明在一次聚会中，不慎遗失了自己的钱包，在接下来的日子，面对小明的将是一系列的补卡手续和堆积的账单… 在小明的百般恳求下，老板最终同意延缓账单的支付时间。可老板又提出，必须从目前还没有支付的所有账单中选出面额最大和最小的两张，并把他们付清。还没有支付的账单会被保留到下一天。 请你帮他计算出支付的顺序。

第1行：一个正整数N(N≤15,000)，表示小明补办银联卡总共的天数。

第2行到第N+1 行：每一行描述一天中收到的帐单。先是一个非负整数M≤100，表示当天收到的账单数，后跟M个正整数（都小于1,000,000,000），表示每张帐单的面额。

输入数据保证每天都可以支付两张帐单。

输出共N 行，每行两个用空格分隔的整数，分别表示当天支付的面额最小和最大的支票的面额。

 【题目分析】

维护一个大顶堆和一个小顶堆，先进行插入操作（向上调整），再进行查询操作（移动并向下调整）。
每次查询一个最大值和最小值进行输出，特殊的：删除大顶堆元素时也要删除小顶堆元素，删除小顶堆元素时也要删除大顶堆元素。

对数据进行二元组，第一元为数据本身，第二元为编号，这样每个数据都是唯一的，当弹出数据后，将相应的编号标记数据赋值为1，后续不能够在进行弹出。

bug：如果第一天只有一组数据，会出现问题。

【代码实现】

#include 

using namespace std;

priority_queue> maxheap, minheap;

int num = 0;
int v[1500005];
int main() {
	//input data
	int n, m;
	cin >> n;
	int x;
	for (int i = 1; i <= n; i++) {
		scanf("%d", &m);
		for (int i = 1; i <= m; i++) {
			scanf("%d", &x);
			maxheap.push(make_pair(x, ++num));
			minheap.push(make_pair(-x, num));
		}
		while (v[maxheap.top().second]) maxheap.pop();
		while (v[minheap.top().second]) minheap.pop();
		printf("%d %d\n", -minheap.top().first, maxheap.top().first);
		v[maxheap.top().second] = v[minheap.top().second] = 1;
		maxheap.pop(), minheap.pop();
	}
	return 0;
}

1373：鱼塘钓鱼(fishing）

【题目描述】

有N个鱼塘排成一排（N<100），每个鱼塘中有一定数量的鱼，例如：N=5时，如下表：

鱼塘编号每1分钟能钓到的鱼的数量（1..1000）每1分钟能钓鱼数的减少量（1..100）当前鱼塘到下一个相邻鱼塘需要的时间（单位：分钟） 

每1分钟能钓到的鱼的数量（1..1000）

每1分钟能钓鱼数的减少量（1..100）

当前鱼塘到下一个相邻鱼塘需要的时间（单位：分钟）

 即：在第1个鱼塘中钓鱼第1分钟内可钓到10条鱼，第2分钟内只能钓到8条鱼，……，第5分钟以后再也钓不到鱼了。从第1个鱼塘到第2个鱼塘需要3分钟，从第2个鱼塘到第3个鱼塘需要5分钟，……

给出一个截止时间T(T<1000)，设计一个钓鱼方案，从第1个鱼塘出发，希望能钓到最多的鱼。

假设能钓到鱼的数量仅和已钓鱼的次数有关，且每次钓鱼的时间都是整数分钟。

【题目分析】

题目理解

方法1 动态规划：确定状态 设f[i][j]为到第i个池塘，第j分钟能够掉到鱼的条数，a[i][j]为第i个池塘j分钟可以掉到鱼的条数,b[i]为从第i-1个池塘到第i个池塘所需的时间    状态转移方程  f[i][j]=max(f[i][j],a[i][k]+f[i-1][j-b[i]-k]) 其中 b[i]<=j<=m   0<=k<=m-b[i]  结果为:f[n][m]

方法2 贪心算法：因为钓鱼不可能走回头路，假定走的最远的池塘为1，可以计算出m个时刻掉到鱼的条数，假定最远池塘为2，总时间k=m-b[1]（从1号池塘都2号池塘的时间），将1号池塘和2号池塘合在一起，取k个较大值相加，假定最远池塘为3，总时间k=m-（b[1]+b[2]），将3个池塘合在一起，取k个较大值相加，。。。。。，只有取n个值的最大值。

小技巧：对于多组已经排好序的数据，取前K个最大的数据，可以每组先取一个（做好标记是第几组），使用优先队列取出最大值，并从最大值的组中取第二大的数放入队列中。 

【代码实现】

动态规划：

#include 
using namespace std;
#define N 105
#define T 1005
int dp[N][T];//dp[i][j]:在前i个鱼塘中钓鱼，消耗时间j，可以钓到鱼的最大数量。
int fish[N], de[N], f[N][T], t[N], st[N], mxTime[N];
int n, endT, mxFish;
int main()
{
	cin >> n;//n:鱼塘数量 
	for(int i = 1; i <= n; ++i)
		cin >> fish[i];//fish[i]:第1分钟第i鱼塘可以钓到的鱼的数量
	for(int i = 1; i <= n; ++i)
		cin >> de[i];//dec[i]:每过一分钟鱼可以钓到的鱼减少的数量
	for(int i = 1; i <= n; ++i)
		for(int j = 1; fish[i] > 0; ++j)
		{
			f[i][j] = f[i][j-1] + fish[i];//f[i][j]:在第i鱼塘钓鱼j分钟能钓到的鱼
			fish[i] -= de[i];
			mxTime[i] = j;//mxTime[i]:在第i鱼塘能钓到鱼的最大时间（超过这一时间就钓不到鱼了） 
		}
	for(int i = 1; i <= n-1; ++i)
	{
		cin >> t[i];//t[i]:从第i鱼塘走到第i+1鱼塘的时间
		st[i+1] = st[i] + t[i];//st[i]:从第1鱼塘走到第i鱼塘的时间 
	}
	cin >> endT;//endT:截止时间 
	for(int i = 1; i <= n; ++i)//i:鱼塘号 
		for(int j = 1; j <= endT; ++j)//j:消耗时间 
			for(int k = 0; k <= mxTime[i] && k <= j-st[i]; ++k)//k：在第j鱼塘钓鱼k分钟 
				dp[i][j] = max(dp[i][j], dp[i-1][j-t[i-1]-k] + f[i][k]);
	for(int i = 1; i <= n; ++i)
		mxFish = max(mxFish, dp[i][endT]);
	cout << mxFish;
	return 0;
}

贪心算法+优先队列：

#include 
#define ll long long
using namespace std;

int n, T, s, a[110], b[110], c[110], t, ans, maxn;

struct cc {
	int x, y;
	bool operator <(const cc &a) const {
		return x < a.x;
	}
} x;

priority_queueq;

int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; i++)scanf("%d", &a[i]);
	for (int i = 1; i <= n; i++)scanf("%d", &b[i]);
	for (int i = 1; i < n; i++)scanf("%d", &c[i]);
	scanf("%d", &T);
	for (int i = 1; i <= n; i++) {

		while (!q.empty())q.pop();
		s = T - t, ans = 0;
		for (int j = 1; j <= i; j++)
			q.push((cc) {
			a[j], j
		});
		while (s > 0 && q.top().x > 0) {
			x = q.top();
			ans = ans + x.x;
			x.x -= b[x.y];
			q.pop();
			q.push(x);
			s--;
		}
		if (maxn < ans)maxn = ans;
		t = t + c[i];
	}
	printf("%d", maxn);
}