树的遍历方式(前中后,层序遍历,递归,迭代,Morris遍历)-----直接查询代码
目录
一.前序遍历
1.递归
2.栈迭代
3.Morris遍历
二.中序遍历
1.递归
2.栈迭代
3.Morris遍历
三.后序遍历
1.递归
2.栈迭代
3.Morris遍历
四.前中后序的统一迭代法
1.前序遍历
2.中序遍历
3.后序遍历
五.层序遍历
1.队列迭代
2.之字形层序遍历
3.锯齿形层序遍历
一.前序遍历
1.递归
ArrayList list = new ArrayList<>();
public List preorderTraversal(TreeNode root) {
preOrder(root);
return list;
}
public void preOrder(TreeNode root) {
if (root != null) {
list.add(root.val);
preOrder(root.left);
preOrder(root.right);
}
} 2.栈迭代
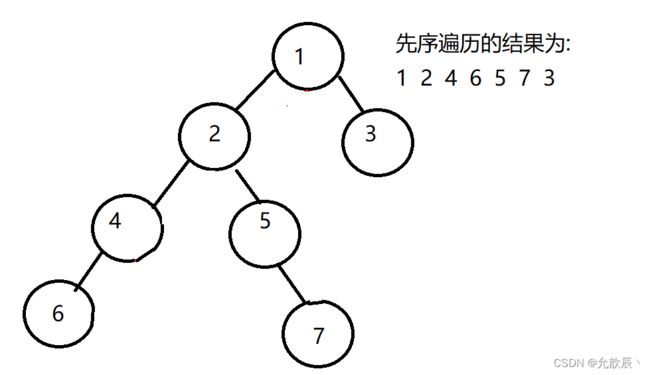
在进行使用栈进行迭代的时候,我们是先入栈右节点,然后入栈左节点,这样做是和栈的结构进行匹配的,因为栈是先进后出的结构,所以先入栈右节点,再入栈左节点,这样出栈的时候左节点才能先出栈
第一次:先入栈1,stack={1}
第二次:然后出栈1,入栈1的右节点3,stack={3},入栈1的左节点2 stack={3,2}
第三次:出栈顶元素2,stack={3},入栈2的右节点,入栈2的左节点.stack={3,5,4}
第四次,出栈顶元素4,stack={3,5},入栈4的左节点6,stack={3,5,6};
第五次:出栈顶元素6,左右结点都为空,没有元素入栈,stack={3,5};
第六次:出栈顶元素5,入栈5的右节点7,stack={3,7};
第七次:出栈顶元素7,,没有元素入栈,stack={3};
第八次,出栈顶元素3,没有元素入栈,stack={};迭代结束
//入栈顺序为,中-->右-->左
public static List preorderTraversal(TreeNode root) {
LinkedList stack = new LinkedList<>();
List res = new ArrayList<>();
if (root == null) {
return res;
}
stack.push(root);
while (!stack.isEmpty()) {
TreeNode pop = stack.pop();
res.add(pop.val);
if (pop.right != null) {
stack.push(pop.right);
}
if (pop.left != null) {
stack.push(pop.left);
}
}
return res;
} 3.Morris遍历
Morris遍历利用了树的线索化,时间复杂度为O(n),空间复杂度为O(1),主要节省了空间,时间复杂度还是不变,具体的分析请看这篇文章:树的前中后序的Morris遍历_允歆辰丶的博客-CSDN博客,这里直接给出代码:
public List preorderTraversal(TreeNode root) {
List res = new ArrayList<>();
TreeNode curr = root;
while (curr != null) {
if (curr.left == null) { // 左子树为空,则输出当前节点,然后遍历右子树
res.add(curr.val);//如果要求直接打印,直接输出System.out.println(curr.val);
curr = curr.right;
} else {
// 找到当前节点的前驱节点
TreeNode prev = curr.left;
while (prev.right != null && prev.right != curr) {
prev = prev.right;
}
if (prev.right == null) {
res.add(curr.val);//如果要求直接打印,直接输出System.out.println(curr.val);
// 将前驱节点的右子树连接到当前节点
prev.right = curr;
curr = curr.left;
} else {
// 前驱节点的右子树已经连接到当前节点,断开连接,输出当前节点,然后遍历右子树
prev.right = null;
curr = curr.right;
}
}
}
return res;
} 二.中序遍历
1.递归
ArrayList list = new ArrayList<>();
public List inorderTraversal(TreeNode root) {
infixOrder(root);
return list;
}
public void infixOrder(TreeNode root) {
if (root != null) {
infixOrder(root.left);
list.add(root.val);
infixOrder(root.right);
}
} 2.栈迭代
中序遍历使用栈迭代还是有一定的难度的.我们可以想一下,前序遍历先遍历的根,栈可以压入根结点,然后再出栈,而中序遍历的话,需要找到最左边的结点,然后才能出栈.这个时候我们可以设置一个cur结点,当cur结点为空的时候出栈出栈,也就是找到了最左端的结点,当cur==null的时候,进行出栈处理,然后开始访问cur的右节点.这样就可以实现中序遍历.
第一种解法:
//入栈顺序: 左-右
public static List inorderTraversal(TreeNode root) {
List res = new ArrayList<>();
if (root == null) {
return res;
}
LinkedList stack = new LinkedList<>();
TreeNode cur = root;
while (cur != null || !stack.isEmpty()) {
if (cur != null) {//cur不为空,说明没有遍历到最左端的叶子结点,也就是第一个输出的结点
stack.push(cur);
cur = cur.left;
} else {
cur = stack.pop();
res.add(cur.val);
cur = cur.right;
}
}
return res;
} 第二种解法:
public List inorderTraversal(TreeNode root) {
ArrayList result = new ArrayList<>();
LinkedList stack = new LinkedList<>();
TreeNode cur = root;
while (cur != null || !stack.isEmpty()) {
while (cur != null) {
stack.push(cur);
cur = cur.left;
}
cur = stack.pop();
result.add(cur.val);
cur = cur.right;
}
return result;
} 3.Morris遍历
具体的分析请看这篇文章:树的前中后序的Morris遍历_允歆辰丶的博客-CSDN博客,这里直接给出代码:
public class InorderThreadedBinaryTree {
private ThreadTreeNode pre = null;
public void threadedNodes(ThreadTreeNode node) {
//如果node==null,不能线索化
if (node == null) {
return;
}
//1、先线索化左子树
threadedNodes(node.left);
//2、线索化当前结点
//处理当前结点的前驱结点
//以8为例来理解
//8结点的.left = null,8结点的.leftType = 1
if (node.left == null) {
//让当前结点的左指针指向前驱结点
node.left = pre;
//修改当前结点的左指针的类型,指向前驱结点
node.leftType = 1;
}
//处理后继结点
if (pre != null && pre.right == null) {
//让当前结点的右指针指向当前结点
pre.right = node;
//修改当前结点的右指针的类型=
pre.rightType = 1;
}
//每处理一个结点后,让当前结点是下一个结点的前驱结点
pre = node;
//3、线索化右子树
threadedNodes(node.right);
}
}
class ThreadTreeNode {
int val;
ThreadTreeNode left;
//0为非线索化,1为线索化
int leftType;
ThreadTreeNode right;
//0为非线索化,1为线索化
int rightType;
public ThreadTreeNode(int val) {
this.val = val;
}
}三.后序遍历
1.递归
ArrayList list = new ArrayList<>();
public List postorderTraversal(TreeNode root) {
postOrder(root);
return list;
}
public void postOrder(TreeNode root) {
if (root != null) {
postOrder(root.left);
postOrder(root.right);
list.add(root.val);
}
} 2.栈迭代
后序遍历可以思考一下前序遍历的迭代代码,后序遍历的遍历顺序为左-->右-->中,我们入栈的顺序为中-->左-->右,然后出栈的顺序为中-->右-->左,这样在最后的时候反转一下,便可以正好符合了后序遍历的顺序了.
第一种解法:
入栈顺序:中-->左-->右 出栈顺序:中-->右-->左
public List postorderTraversal(TreeNode root) {
List res = new ArrayList<>();
if (root == null) {
return res;
}
LinkedList stack = new LinkedList<>();
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
res.add(node.val);
if (node.left != null) {
stack.push(node.left);
}
if (node.right != null) {
stack.push(node.right);
}
}
Collections.reverse(res);
return res;
} 第二种解法:
public List postorderTraversal(TreeNode root) {
ArrayList result = new ArrayList<>();
LinkedList stack = new LinkedList<>();
TreeNode cur=root,pre=null;
while (cur!=null||!stack.isEmpty()) {
while(cur!=null){
stack.push(cur);
cur=cur.left;
}
cur = stack.pop();
if(cur.right==null||pre==cur.right){
result.add(cur.val);
pre=cur;
cur=null;
}else{
stack.push(cur);
cur = cur.right;
}
}
return result;
} 3.Morris遍历
具体的分析请看这篇文章:树的前中后序的Morris遍历_允歆辰丶的博客-CSDN博客,这里直接给出代码:
public List postorderTraversal(TreeNode root) {
List res = new ArrayList<>();
TreeNode dump = new TreeNode(0);//建立一个临时结点
dump.left = root; //设置dump的左节点为root
TreeNode curr = dump; //当前节点为dump
while (curr != null) {
if (curr.left == null) { // 左子树为空,则输出当前节点,然后遍历右子树
curr = curr.right;
} else {
// 找到当前节点的前驱节点
TreeNode prev = curr.left;
while (prev.right != null && prev.right != curr) {
prev = prev.right;
}
if (prev.right == null) {
// 将前驱节点的右子树连接到当前节点
prev.right = curr;
curr = curr.left;
} else {
reverseAddNodes(curr.left, prev, res);
// 前驱节点的右子树已经连接到当前节点,断开连接,输出当前节点,然后遍历右子树
prev.right = null;
curr = curr.right;
}
}
}
return res;
}
private void reverseAddNodes(TreeNode begin, TreeNode end, List res) {
reverseNodes(begin, end); //将begin到end的进行逆序连接
TreeNode curr = end;
while (true) {//将逆序连接后端begin到end添加
res.add(curr.val);
if (curr == begin)
break;
curr = curr.right;
}
reverseNodes(end, begin);//恢复之前的连接状态
}
/**
* 将begin到end的进行逆序连接
*
* @param begin
* @param end
*/
private void reverseNodes(TreeNode begin, TreeNode end) {
TreeNode prev = begin;
TreeNode curr = prev.right;
TreeNode post;
while (prev != end) {
post = curr.right;
curr.right = prev;
prev = curr;
curr = post;
}
} 四.前中后序的统一迭代法
1.前序遍历
我们为了同时解决访问节点(遍历节点)和处理节点(将元素放进结果集)不一致的情况,我们加入标记节点null,当出栈的结点为为null的时候,我们将再次出栈的元素加入到res结合中,
因为栈的性质:先进后出,所以在加入到栈的时候,前序要遵循右-->左-->中(做标记加入null)的顺序加入到栈,然后出栈为null结点的时候,处理结点,将元素放进结果集.
public static List preorderTraversal(TreeNode root) {
LinkedList stack = new LinkedList<>();
List res = new ArrayList<>();
if (root != null) {
stack.push(root);
}
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
if (node != null) {
if (node.right != null)
stack.push(node.right); // 添加右节点(空节点不入栈)
if (node.left != null)
stack.push(node.left); // 添加左节点(空节点不入栈)
stack.push(node); // 添加中节点
stack.push(null); // 中节点访问过,但是还没有处理,加入空节点做为标记。
} else { // 只有遇到空节点的时候,才将下一个节点放进结果集
node = stack.pop(); // 重新取出栈中元素
res.add(node.val); // 加入到结果集
}
}
return res;
} 2.中序遍历
因为栈的性质:先进后出,所以在加入到栈的时候,前序要遵循右-->中(做标记加入null)-->左的顺序加入到栈,然后出栈为null结点的时候,处理结点,将元素放进结果集.
public List inorderTraversal(TreeNode root) {
List res = new LinkedList<>();
LinkedList stack = new LinkedList<>();
if (root != null)
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
if (node != null) {
if (node.right != null)
stack.push(node.right); // 添加右节点(空节点不入栈)
stack.push(node); // 添加中节点
stack.push(null); // 中节点访问过,但是还没有处理,加入空节点做为标记。
if (node.left != null)
stack.push(node.left); // 添加左节点(空节点不入栈)
} else { // 只有遇到空节点的时候,才将下一个节点放进结果集
node = stack.pop(); // 取出栈中元素
res.add(node.val); // 加入到结果集
}
}
return res;
} 3.后序遍历
因为栈的性质:先进后出,所以在加入到栈的时候,前序要遵循中(做标记加入null)-->右-->左的顺序加入到栈,然后出栈为null结点的时候,处理结点,将元素放进结果集.
public List postorderTraversal(TreeNode root) {
List res = new LinkedList<>();
LinkedList stack = new LinkedList<>();
if (root != null)
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
if (node != null) {
stack.push(node); // 添加中节点
stack.push(null); // 中节点访问过,但是还没有处理,加入空节点做为标记。
if (node.right != null)
stack.push(node.right); // 添加右节点(空节点不入栈)
if (node.left != null)
stack.push(node.left); // 添加左节点(空节点不入栈)
} else { // 只有遇到空节点的时候,才将下一个节点放进结果集
node = stack.pop(); // 重新取出栈中元素
res.add(node.val); // 加入到结果集
}
}
return res;
} 五.层序遍历
1.队列迭代
层序遍历主要是利用了队列先进后出的性质,每一次的循环次数为为当前层的结点的个数,在遍历的当前层的结点的同时,如果左右孩子不为空的话,入队当前结点的左右孩子结点,直到队列里面没有元素.例如:
第一次先根结点入队列:queue={1};
第二次:1结点出队列,然后将1的左右节点2结点和3结点入队列,queue={2,3};
第三次:2结点出队列,4和5结点入队列,3出队列,3无左右节点,queue={4,5};
第四次:4结点出队列,4的左节点入队列,5结点出队列,5的右节点入队列,queue={6,7}
第五次,6,7结点出队列,因为他们都没有左右节点,因此queue=null,遍历结束
public List> levelOrder(TreeNode root) {
List> list = new ArrayList<>();
if (root == null)
return list;
LinkedList queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
int size = queue.size();
List res = new ArrayList<>();
for (int i = 0; i < size; ++i) {
TreeNode node = queue.poll();
res.add(node.val);
if (node.left != null)
queue.offer(node.left);
if (node.right != null)
queue.offer(node.right);
}
list.add(res);
}
return list;
} 2.之字形层序遍历
用两个栈实现之字形(Z字形)打印,如下图的遍历顺序,一个栈是正向存储每层的元素,一个栈逆向存储每层的元素,当然也可以使用一个队列完成
public static List zprintf(TreeNode root) {
LinkedList stack1 = new LinkedList<>();
LinkedList stack2 = new LinkedList<>();
ArrayList list = new ArrayList<>();
boolean flag = false;
if (root != null)
stack1.push(root);
while (!stack2.isEmpty() || !stack1.isEmpty()) {
if (!flag) {
TreeNode node = stack1.pop();
list.add(node.val);
if (node.left != null)
stack2.push(node.left);
if (node.right != null)
stack2.push(node.right);
if (stack1.isEmpty()) {
flag = true;
}
} else {
TreeNode node = stack2.pop();
list.add(node.val);
if (node.right != null)
stack1.push(node.right);
if (node.left != null)
stack1.push(node.left);
if (stack2.isEmpty()) {
flag = false;
}
}
}
return list;
} 3.锯齿形层序遍历
力扣:力扣
-
如果从左至右,我们每次将被遍历到的元素插入至双端队列的末尾。
-
如果从右至左,我们每次将被遍历到的元素插入至双端队列的头部。
public List> zigzagLevelOrder(TreeNode root) {
List> ans = new ArrayList<>();
LinkedList queue = new LinkedList<>();
boolean isOrderLeft = true;
if (root == null)
return ans;
queue.push(root);
while (!queue.isEmpty()) {
LinkedList levelList = new LinkedList<>();
int size = queue.size();
for (int i = 0; i < size; ++i) {
TreeNode node = queue.poll();
if(isOrderLeft){
levelList.offer(node.val);
}else {
levelList.push(node.val);
}
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
ans.add(levelList);
isOrderLeft = !isOrderLeft;
}
return ans;
} 方法二:
public ArrayList> Print(TreeNode pRoot) {
LinkedList queue = new LinkedList<>();
ArrayList> res = new ArrayList<>();
if (pRoot != null)
queue.offer(pRoot);
while (!queue.isEmpty()) {
// 打印奇数层
ArrayList temp = new ArrayList<>();
int size = queue.size();
//正向
for (int i = 0; i < size; ++i) {
// 从左向右打印
TreeNode node = queue.removeFirst();
temp.add(node.val);
// 先左后右加入下层节点
if (node.left != null)
queue.addLast(node.left);
if (node.right != null)
queue.addLast(node.right);
}
res.add(temp);
if (queue.isEmpty())
break; // 若为空则提前跳出
// 打印偶数层
temp = new ArrayList<>();
size = queue.size();
//逆向
for (int i = 0; i < size; ++i) {
// 从右向左打印
TreeNode node = queue.removeLast();
temp.add(node.val);
// 先右后左加入下层节点
if (node.right != null)
queue.addFirst(node.right);
if (node.left != null)
queue.addFirst(node.left);
}
res.add(temp);
}
return res;
}