Transformer
目录
1.引言
2.快速回顾注意力
3.Transformer架构
3.1.编码器和解码器组件
3.1.1.编码器
3.1.2解码器
3.2.Transformer中的模块
3.3.注意模块
3.3.1.缩放点积注意事项
3.3.2多头注意
3.4.Transformer中的注意事项
3.4.1.自注意
3.4.2自回归或因果注意
3.4.3.交叉注意
3.5.FFN
3.6.残差连接和归一化
3.7.位置编码
3.7.1.绝对位置信息
3.7.2.相对位置信息
4.使用自注意背后的动机
5.目前的研究
6.问题
7.总结
8.TransformerX库
9.参考文献
1.引言
作为人工智能研究过程中的一个成功前沿,Transformer被认为是一种新型的深度前馈人工神经网络架构,它利用了自注意机制,可以处理输入序列项之间的长期相关性。
由于其在行业和学术研究中的巨大成功,研究人员自2017年Vaswani等人提出了丰富的Transformer架构[3],并在大量领域中采用,如自然语言处理(NLP)、计算机视觉(CV)、,音频和语音处理、化学和生命科学;他们可以在前面提到的学科中实现SOTA性能。
在本文中,通过底层数学、python代码实现和不同层的可视化来解释了Transformer架构。端到端示例可在GitHub上的TransformerX库存储库中找到。
https://github.com/tensorops/TransformerX
2.快速回顾注意力
较低层次的概念,如与编码器-解码器模型相关的注意力机制和术语,是Transformer的基本思想。因此,我简要总结了这些方法。
注意力是一种处理能力有限的认知资源分配方案 [1]。
Bahdanau等人[2]提出的注意背后的一般思想是,当在每个步骤中翻译单词时,它搜索位于输入序列中不同位置的最相关信息。
在下一步中,它同时生成源标记(单词)的翻译,1)这些相关位置的上下文向量和2)先前生成的单词。
可以根据以下几个标准将其分类为各种类别:
注意力的特性:
1.软 2.硬 3.局部 4.全局
输入特征的形式:
1.Item-wise 2. Location-wise
输入表示:
1.Co-attention 2. Self-attention 3. Distinctive attention 4. Hierarchical attention
输出表示:
1.多头 2.单输出 3.多维
如果你觉得注意力机制处于未知领域,我建议你阅读以下文章:
https://towardsdatascience.com/rethinking-thinking-how-do-attention-mechanisms-actually-work-a6f67d313f99
3.Transformer架构
基本Transformer[3]架构由两个主要构建块组成,即编码器和解码器块。
编码器从输入表示序列 (₁ , ..., ₙ) 生成嵌入向量 = (₁ , ..., ₙ),并将其传递给解码器以生成输出序列 (₁ , ..., ₘ).
在每一步生成输出之前, 向量被送入解码器,因此该模型是自回归的。
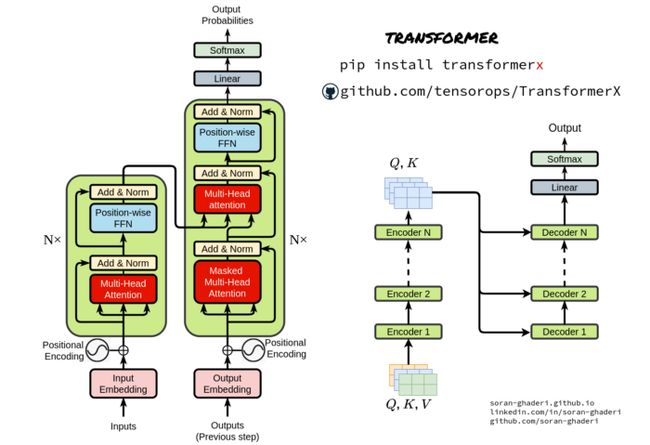
3.1.编码器和解码器组件
与序列到序列模型类似,Transformer使用编码器-解码器架构。
3.1.1.编码器
编码器只是多个组件或层的堆栈- 在原始论文中是6。它们本身是两个子层,即多头自注意块和简单FC FFN(全连接的前馈网络)。
为了实现更深入的模型,研究人员通过包裹两个子层,然后进行层归一化,并实现残差连接。因此,每个子层的输出都是LayerNorm( + Sublayer( )) ,Sublayer(* *)*是在其内部实现的函数。所有子层以及嵌入的输出维度为 _model=512。
Transformer编码器块的实现:
# Visit TransformerX on github (https://github.com/tensorops/TransformerX) for more
# Join TensorOps community on Discord: https://discord.com/invite/7BF9KUnBNT
import tensorflow as tf
from transformerx.layers import PositionalEncoding
from transformerx.layers import TransformerEncoderBlock
class TransformerEncoder(tf.keras.layers.Layer):
"""Transformer encoder that encompasses one or more TransformerEncoderBlock blocks."""
def __init__(
self,
vocab_size,
depth,
norm_shape,
ffn_num_hiddens,
num_heads,
n_blocks,
dropout,
bias=False,
):
super().__init__()
self.depth = depth
self.n_blocks = n_blocks
self.embedding = tf.keras.layers.Embedding(vocab_size, depth)
self.pos_encoding = PositionalEncoding(depth, dropout)
self.blocks = [
TransformerEncoderBlock(
depth,
norm_shape,
ffn_num_hiddens,
num_heads,
dropout,
bias,
)
for _ in range(self.n_blocks)
]
def call(self, X, valid_lens, **kwargs):
# Since positional encoding values are between -1 and 1, the embedding
# values are multiplied by the square root of the embedding dimension
# to rescale before they are summed up
X = self.pos_encoding(
self.embedding(X) * tf.math.sqrt(tf.cast(self.depth, dtype=tf.float32)),
**kwargs,
)
self.attention_weights = [None] * len(self.blocks)
for i, block in enumerate(self.blocks):
X = block(X, valid_lens, **kwargs)
self.attention_weights[i] = block.attention.attention.attention_weights
return3.1.2解码器
除了编码器中使用的子层之外,解码器对编码器组件的输出应用多头注意。与编码器一样,残差连接连接到子层,然后进行层规范化。保证对该位置的预测 可以仅依赖于先前已知的位置,对自注意子层应用另一种修改以防止位置伴随着将输出嵌入偏移一个位置而注意其他位置。
Transformer解码器块的实现:
# Visit TransformerX on github (https://github.com/tensorops/TransformerX) for more
# Join TensorOps community on Discord: https://discord.com/invite/7BF9KUnBNT
import tensorflow as tf
from transformerx.layers import PositionalEncoding
from transformerx.layers import TransformerDecoderBlock
class TransformerDecoder(tf.keras.layers.Layer):
"""Transformer decoder that encompasses one or more TransformerDecoderBlock blocks."""
def __init__(
self,
vocab_size,
depth,
norm_shape,
ffn_num_hiddens,
num_heads,
n_blocks,
dropout,
):
super().__init__()
self.depth = depth
self.n_blocks = n_blocks
self.embedding = tf.keras.layers.Embedding(vocab_size, depth)
self.pos_encoding = PositionalEncoding(depth, dropout)
self.blocks = [
TransformerDecoderBlock(
depth,
norm_shape,
ffn_num_hiddens,
num_heads,
dropout,
i,
)
for i in range(n_blocks)
]
self.dense = tf.keras.layers.Dense(vocab_size)
def init_state(self, enc_outputs, enc_valid_lens):
return [enc_outputs, enc_valid_lens, [None] * self.n_blocks]
def call(self, X, state, **kwargs):
X = self.pos_encoding(
self.embedding(X) * tf.math.sqrt(tf.cast(self.depth, dtype=tf.float32)),
**kwargs,
)
# 2 attention layers in decoder
self._attention_weights = [[None] * len(self.blocks) for _ in range(2)]
for i, block in enumerate(self.blocks):
X, state = block(X, state, **kwargs)
# Decoder self-attention weights
self._attention_weights[0][i] = block.attention1.attention.attention_weights
# Encoder-decoder attention weights
self._attention_weights[1][i] = block.attention2.attention.attention_weights
return self.dense(X), state
@property
def attention_weights(self):
return self._attention_weights3.2.Transformer中的模块
接下来,我将讨论构成原始Transformer架构的基本组件。
注意模块
前馈网络
残差连接和归一化
位置编码
3.3.注意模块
该Transformer将信息检索中的查询键值(QKV)概念与注意力机制相结合
缩放的点积注意
多头注意力
3.3.1.缩放点积注意事项
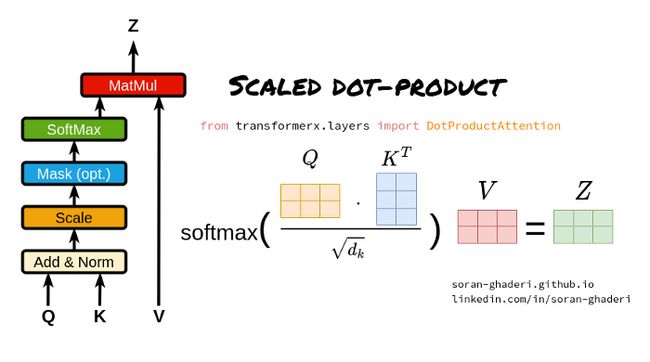
缩放点积注意力公式如下:

其中 ∈ ℝ^×, ∈ ℝ^ ×, 和 ∈ ℝ^ × 是表示矩阵。键(或值)和查询的长度由 和 并且它们的尺寸为 和.、
矩阵 在等式1中,通常称为注意力矩阵。他们使用点积注意力而不是加法注意力(使用具有单个隐藏层的前馈网络来计算兼容性函数)的原因是,由于矩阵乘法优化技术,速度和空间效率更快。
尽管如此,对于较大值的 这将softmax函数的梯度推到极小的梯度。为了抑制softmax函数的梯度消失问题,将键和查询的点积除以, 由于这个事实,它被称为缩放点积。
点积注意块的实现:
# Visit TransformerX on github (https://github.com/tensorops/TransformerX) for more
# Join TensorOps community on Discord: https://discord.com/invite/7BF9KUnBNT
import tensorflow as tf
import transformerx as tx
class DotProductAttention(tf.keras.layers.Layer):
"""Scaled dot product attention."""
def __init__(self, dropout, num_heads=8):
super().__init__()
self.dropout = tf.keras.layers.Dropout(dropout)
self.num_heads = num_heads # To be covered later
def call(self, queries, keys, values, **kwargs):
d = queries.shape[-1]
scores = tf.matmul(queries, keys, transpose_b=True) / tf.math.sqrt(
tf.cast(d, dtype=tf.float32)
)
self.attention_weights = tx.utils.masked_softmax(scores)
return tf.matmul(self.dropout(self.attention_weights, **kwargs), values)3.3.2多头注意

引入多个注意力头而不是单个注意力函数,Transformer 将 维的原始查询、键和值线性投影到 、 和 维度,分别使用不同的线性投影 h次;通过它,可以并行计算这些投影上的注意力函数(等式 1),产生 维输出值。然后该模型将它们连接起来并生成 维表示。
哪里
其中ᵢ ∈ ℝ^d_model×dk, ᵢ ∈ ℝ^d_model×dk, ᵢ ∈ ℝ^d_model×dv, 和 ∈ ℝ^h*dv×d_model 。
该过程使Transformer能够共同处理不同的表示子空间和位置。为了使它更具体,对于一个特定的形容词,一个头部可能会捕捉到形容词的强度,而另一个头部则可能会注意到它的消极性和积极性。
多头注意的实现
# Visit TransformerX on github (https://github.com/tensorops/TransformerX) for more
# Join TensorOps community on Discord: https://discord.com/invite/7BF9KUnBNT
import tensorflow as tf
import transformerx as tx
class MultiHeadAttention(tf.keras.layers.Layer):
"""Multi-head attention."""
def __init__(
self,
d_model,
num_heads,
dropout,
bias=False,
**kwargs,
):
super(MultiHeadAttention, self).__init__()
self.num_heads = num_heads
self.attention = tx.layers.DotProductAttention(dropout, num_heads)
self.W_q = tf.keras.layers.Dense(d_model, use_bias=bias)
self.W_k = tf.keras.layers.Dense(d_model, use_bias=bias)
self.W_v = tf.keras.layers.Dense(d_model, use_bias=bias)
self.W_o = tf.keras.layers.Dense(d_model, use_bias=bias)
def split_heads(self, X: tf.Tensor) -> tf.Tensor:
X = rearrange(X, "b h (heads hidden) -> b h heads hidden", heads=self.num_heads)
X = rearrange(X, "b d1 d2 d3 -> b d2 d1 d3")
X = rearrange(X, "b d1 d2 d3 -> (b d1) d2 d3")
return X
def inverse_transpose_qkv(self, X):
"""Reverse the operation of split_heads."""
X = tf.reshape(X, shape=(-1, self.num_heads, X.shape[1], X.shape[2]))
X = tf.transpose(X, perm=(0, 2, 1, 3))
return tf.reshape(X, shape=(X.shape[0], X.shape[1], -1))
def call(self, queries, values, keys, valid_lens, window_mask=None, **kwargs):
# Shape of queries, keys, or values:
# (batch_size, no. of queries or key-value pairs, depth)
# Shape of valid_lens: (batch_size,) or (batch_size, no. of queries)
# After transposing, shape of output queries, keys, or values:
# (batch_size * num_heads, no. of queries or key-value pairs,
# depth / num_heads)
queries = self.split_heads(self.W_q(queries))
keys = self.split_heads(self.W_k(keys))
values = self.split_heads(self.W_v(values))
# Shape of output: (batch_size * num_heads, no. of queries,
# depth / num_heads)
output = self.attention(
queries, keys, values, valid_lens, window_mask, **kwargs
)
# Shape of output_concat: (batch_size, no. of queries, depth)
output_concat = self.inverse_transpose_qkv(output)
return self.W_o(output_concat)可以看出,多头注意力有三个决定张量维度的超参数:
注意头数
模型大小(嵌入大小):嵌入向量的长度。
查询、键和值大小:输出查询、键矩阵和值矩阵的线性层使用的查询、键权重和值权重大小
3.4.Transformer中的注意事项
在最初的Transformer论文中采用了三种不同的使用注意力的方法,它们在键、查询和值被输入注意力函数的方式方面是不同的。
自注意
屏蔽的自注意(自回归或因果注意)
交叉注意
3.4.1.自注意
所有键、查询和值向量来自相同的序列,在Transformer的情况下,编码器的前一步输出,允许编码器同时注意其自身前一层中的所有位置,即。 = = = (以前的编码器输出)。

3.4.2掩蔽的自注意(自回归或因果注意)
尽管有编码器层,但在解码器的自注意中,查询被限制在它们之前的键值对位置以及它们的当前位置,以便保持自回归特性。这可以通过屏蔽无效位置并将其设置为负无限来实现,即 = −∞ 如果 < .
3.4.3.交叉注意
这种类型的注意力从先前的解码器层获得其查询,而键和值是从编码器产量获得的。这基本上是在序列到序列模型中的编码器-解码器注意机制中使用的注意。换句话说,交叉注意力将两个不同的嵌入序列相结合,这些维度从一个序列中导出其查询,从另一个序列导出其键和值。
假设S1和S2是两个嵌入序列,交叉注意力从S1获得其键和值,从S2获得其查询,然后计算注意力得分并生成长度为S2的结果序列。在Transformer的情况下,键和值是从编码器和前一步解码器输出的查询中导出的。

值得一提的是,两个输入嵌入序列可以是不同的形式(即文本、图像、音频等)。
3.5.FFN
在编码器和解码器中的每个子层的顶部,按全连接的前馈网络以完全相同的方式单独应用于每个位置,但是,各层的参数不同。它是一对线性层,其间具有ReLU激活函数;它与核大小为1的两层卷积相同。
其中x是前一层的输出,以及₁ ∈ ℝ^_model × , ₂ ∈ ℝ^ × _model, ₁ ∈ ℝ^, ₂ ∈ ℝ^_model 是可训练的矩阵
FFN的实现:
# Visit TransformerX on github (https://github.com/tensorops/TransformerX) for more
# Join TensorOps community on Discord: https://discord.com/invite/7BF9KUnBNT
import tensorflow as tf
class PositionWiseFFN(tf.keras.layers.Layer):
"""Position-wise feed-forward network."""
def __init__(self, ffn_num_hiddens, ffn_num_outputs):
super().__init__()
self.dense1 = tf.keras.layers.Dense(ffn_num_hiddens)
self.relu = tf.keras.layers.ReLU()
self.dense2 = tf.keras.layers.Dense(ffn_num_outputs)
def call(self, X):
# x.shape: (batch size, number of time steps or sequence length in tokens, depth)
return self.dense2(self.relu(self.dense1(X)))3.6.残差连接和归一化
用残差连接包裹每个模块可以实现更深的架构,同时避免梯度消失/爆炸。因此,Transformer在模块周围使用残差连接,然后进行层规范化。其公式如下:
′ = LayerNorm(SelfAttention() + )
= LayerNorm(FFN( ' ) + ' )
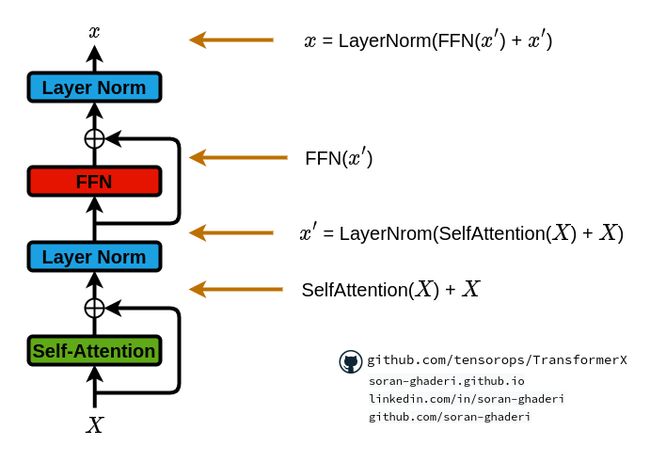
残差连接和标准化的实现:
# Visit TransformerX on github (https://github.com/tensorops/TransformerX) for more
# Join TensorOps community on Discord: https://discord.com/invite/7BF9KUnBNT
import tensorflow as tf
class AddNorm(tf.keras.layers.Layer):
"""Add a residual connection followed by a layer normalization"""
def __init__(self, norm_shape, dropout):
super(AddNorm, self).__init__()
self.dropout = tf.keras.layers.Dropout(dropout)
self.ln = tf.keras.layers.LayerNormalization(norm_shape)
def call(self, X, Y, **kwargs):
return self.ln(self.dropout(Y, **kwargs) + X)3.7.位置编码
Transformer的研究人员使用了一个有趣的想法,将有序注入到输入token中,因为它没有递归或卷积。绝对和相对位置信息可以用来暗示输入的顺序,可以学习或固定。矩阵之间的求和过程需要相同大小的矩阵,因此,位置编码维度与输入嵌入的维度相同。它们被输入到编码器和解码器模块底部的输入编码中。
Vaswani等人[3]在正弦和余弦函数的帮助下使用了固定位置编码-然而,他们尝试了相对位置编码,并意识到在他们的情况下,它产生了几乎相同的结果[4]。
是包含n个d维嵌入标记的输入表示。位置编码后为 + , 是相同大小的位置嵌入矩阵。第i行的元素的第2列或第(2+1) 列为:
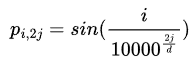
和

在位置嵌入矩阵P中,行表示token在序列中的位置,列表示不同的位置编码维度。
# Visit TransformerX on github (https://github.com/tensorops/TransformerX) for more
# Join TensorOps community on Discord: https://discord.com/invite/7BF9KUnBNT
import numpy as np
import tensorflow as tf
class PositionalEncoding(tf.keras.layers.Layer):
def __init__(self, num_hiddens, dropout, max_len=1000):
super().__init__()
self.dropout = tf.keras.layers.Dropout(dropout)
self.P = np.zeros((1, max_len, num_hiddens))
print("P.shape", self.P.shape)
X = np.arange(max_len, dtype=np.float32).reshape(-1, 1) / np.power(
10000, np.arange(0, num_hiddens, 2, dtype=np.float32) / num_hiddens
)
self.P[:, :, 0::2] = tf.sin(
X
) # x[low::stride] -> positions: 0, 2, 4, ... of all rows and columns
self.P[:, :, 1::2] = tf.cos(
X
) # x[low::stride] -> positions: 1, 3, 5 , ... of all rows and columns
def call(self, X, **kwargs):
X = X + self.P[:, : X.shape[1], :]
return self.dropout(X, **kwargs)我在下面的可视化中描述了矩阵 中 4 列之间的差异。注意不同列的不同频率。
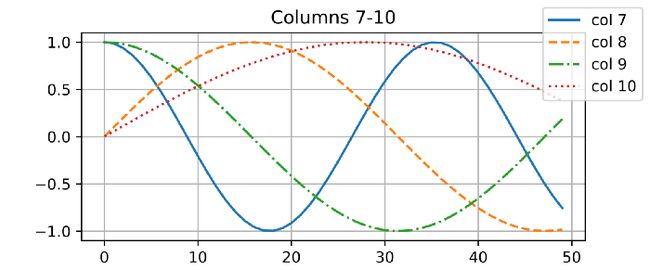
3.7.1.绝对位置信息
在位置编码类型中,频率基于元素的位置而变化。
举个例子,看看下面的二进制编码;数值小(右侧)的数字波动更频繁,即数值大的更稳定。
0 -> 000
1 -> 001
2 -> 010
3 -> 011
4 -> 100
5 -> 101
6 -> 110
7 -> 1113.7.2.相对位置信息
除了上述位置编码之外,另一种方法是学习通过相对位置来。对于任何固定位置, 位置编码+ 可以通过将其线性投影到位置来得到。

4.使用自注意背后的动机
“Attention is All You Need[3]论文中的研究人员在将自注意力与卷积层和循环层进行比较时考虑了多个标准。这些需求可分为三大类:

计算复杂性:每层计算复杂性的总量
并行化:计算可以在多大程度上并行化
学习长期依赖:处理网络中长期依赖的能力
可解释性:检查学习分布的能力,以及注意输入的语义和句法特征的能力
5.研究前沿
最近的变体试图通过进一步探索改进架构的不同路线来提高原著的性能,即:
效率:在处理长序列时,自注意力会导致计算和记忆复杂性,这促使研究人员通过引入轻量级注意力解决方案(如稀疏注意力)和分而治之方法(如递归和分层机制)来解决这一问题。
泛化:由于Transformer对输入数据的结构偏差不敏感,因此需要大量的数据进行训练,因此,已经采取了诸如引入结构偏差或正则化、对大规模未标记数据进行预训练等措施来应对这一障碍。
适应:由于Transformer能够被各个领域采用,研究人员试图将其与特定的下游任务结合起来。
6.问题
在本节中,我邀请你思考以下问题。
如果用Transformer中的附加注意力代替缩放的点积注意力,会发生什么?
如果我们想使用Transformer进行语言建模,我们应该使用编码器、解码器,还是两者都使用?
如果Transformer的输入过长会发生什么?我们该怎么处理?
我们可以做什么来提高Transformer的计算和存储效率?
7.总结
在本文中,你了解了Transformer架构及其实现,并看到了它在不同领域(如机器翻译、计算机视觉以及其他一些学科)带来的重大突破,同时降低了它们的复杂性,并使它们更易于解释。
Transformer的另一个基本组件是不同头部的并行化能力,因为它纯粹使用多头自注意,而不是使用递归或卷积层。现在你已经熟悉了Transformer的主要组件。
感谢阅读!
8.TransformerX库
TransformerX是一个python库,为研究人员、学生和专业人员提供开发、训练和评估Transformer所需的构建块,并顺利集成到Tensorflow中(我们将很快添加对Pytorch和JAX的支持)。
我们正在积极努力添加更多令人惊叹的功能。(我们最近发布了它的第一个版本)
https://github.com/tensorops/TransformerX
9.参考文献
[1] J. R. Anderson, 2005, Cognitive Psychology and Its Implications, Worth Publishers, 2005.
[2] D. Bahdanau, K. Cho, Y. Bengio, Neural machine translation by jointly learning to align and translate, in: ICLR.
[3] Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Łukasz Kaiser, and Illia Polosukhin. Attention is all you need. NeurIPS, 2017.
[4] Jonas Gehring, Michael Auli, David Grangier, Denis Yarats, and Yann N. Dauphin. Convolutional sequence to sequence learning. arXiv preprint arXiv:1705.03122v2, 2017.
[5] Yonghui Wu, Mike Schuster, Zhifeng Chen, Quoc V Le, Mohammad Norouzi, Wolfgang Macherey, Maxim Krikun, Yuan Cao, Qin Gao, Klaus Macherey, et al. Google’s neural machine translation system: Bridging the gap between human and machine translation. arXiv preprint arXiv:1609.08144, 2016.
[6] Denny Britz, Anna Goldie, Minh-Thang Luong, and Quoc V. Le. Massive exploration of neural machine translation architectures. CoRR, abs/1703.03906, 2017.
[7] Nal Kalchbrenner, Lasse Espeholt, Karen Simonyan, Aaron van den Oord, Alex Graves, and Koray Kavukcuoglu. Neural machine translation in linear time. arXiv preprint arXiv:1610.10099v2, 2017.
☆ END ☆
如果看到这里,说明你喜欢这篇文章,请转发、点赞。微信搜索「uncle_pn」,欢迎添加小编微信「 woshicver」,每日朋友圈更新一篇高质量博文。
↓扫描二维码添加小编↓

