ARIMA-GRNN模型的发病率预测GUI：基于Matlab编写（ARIMA部分）

       该软件首先通过经典的ARIMA模型得出初步的预测数值，生成绝对误差序列，然后输入GRNN模型得出预测的绝对误差数值，最后通过反算生成最终预测数值。

第一步、Matlab支持插件的安装

1. 双击MCRInstaller.exe安装

2. 自动解压：

3. 无脑点击下一步

4. 安装完成。

第二步、构建ARIMA模型

一、构建ARIMA模型 进入ARIMA模型图形用户界面（GUI）；

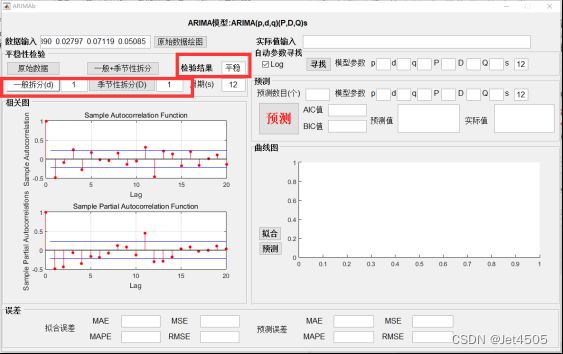
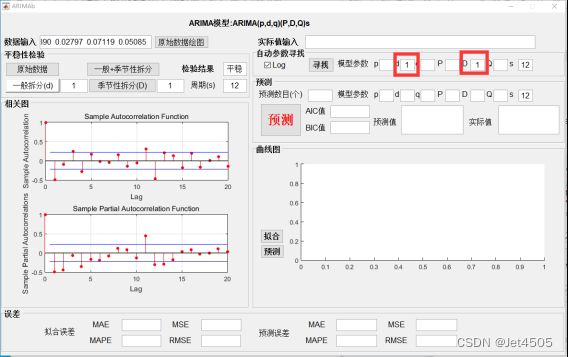
1.界面介绍

1.1.数据输入 输入用于预测的原始数据，如下图。

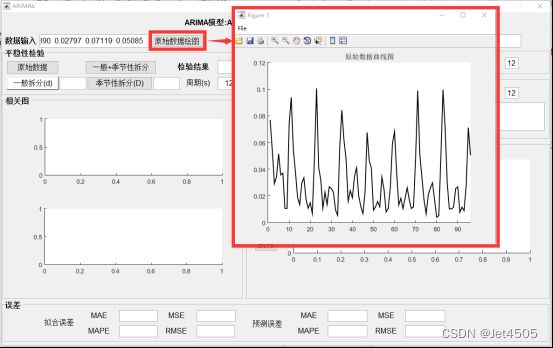
1.2.原始数据绘图 点击弹出原始数据曲线图，以便观察数据的消长趋势以及周期性。

1.3.实际值输入 如果用于测试模型的预测精度，此时要预测的数据已知，则输入该数据集。如果用于预测数据，则要预测的数据未知，此时全部输入0。例如要预测6个数据，则需输入6个0。

1.4.平稳检验和相关图模块

1.4.1.原始数据 点击原始数据按钮，在相关图模块显示原始数据的自相关图以及偏相关图，并在显示检验结果（是否平稳）。

1.4.2.一般拆分 填入拆分次数，点击一般拆分按钮，在相关图模块显示经过一般拆分数据的自相关图以及偏相关图，并在显示检验结果（是否平稳）；拆分次数即为d值。

1.4.2.季节性拆分 填入拆分次数，点击季节性拆分按钮，在相关图模块显示经过季节性拆分数据的自相关图以及偏相关图，并在显示检验结果（是否平稳）；拆分次数即为D值。

1.4.3.一般+季节性拆分 点击一般+季节性拆分按钮，在相关图模块显示经过一般和季节性拆分数据的自相关图以及偏相关图，并在显示检验结果（是否平稳）。

1.5.自动参数寻找模块

1.5.1.Log 勾选后，原始数据经过Log变换。此选项影响所有步骤，包括平稳性检验、模型构建、拟合和预测。

1.5.2寻找 必须手动输入参数d和D，周期s默认为12，可以根据实际情况修改。点击寻找按钮后，程序自动寻找最优p、q、P、Q参数（四个参数取值均从0至3）；并将最优参数值输出。

1.6.预测模块 

1.6.1.预测数目（个） 显示需要预测数据的个数，程序自动从实际值输入文本框识别个数并输出。

1.6.2.模型参数 输入模型7个参数，其中周期s默认为12，可以根据需要修改。

1.6.3.预测 点击预测按钮后，输出AIC值、BIC值、预测值、实际值，弹出模型参数检验的窗口，并在曲线图模块显示实际值和预测值的曲线图，在误差模块显示预测误差的四个指标。

1.7.曲线图模块

1.7.1.拟合 点击拟合按钮后，显示模型拟合效果曲线图，并在误差模块输出拟合误差的四个指标，弹出显示模型具体拟合值的窗口。

1.7.2.预测 点击拟合按钮后，显示模型拟合效果曲线图，并在误差模块输出拟合误差的四个指标。

1.8.误差模块

1.8.1.拟合误差 MAE 输出模型预测的平均绝对误差；

          MAPE 输出模型预测的平均相对误差；

          MSE 输出模型预测的均方误差；

          RMSE 输出模型预测的均方根误差。

1.8.2.预测误差 MAE 输出模型预测的平均绝对误差；

          MAPE 输出模型预测的平均相对误差；

          MSE 输出模型预测的均方误差；

          RMSE 输出模型预测的均方根误差。

1.9重置 清空所有窗口，进行下一组数据操作。

图1 ARIMA软件界面 下载地址

二、基于实例文献进行操作演示

数据来源于Wei Wu等[1]运用组合模型对江苏省HFRS月发病率进行预测。江苏省2004年1月至2012年12月HFRS月发病率如图1所示。本文使用2004年1月至2011年12月HFRS月发病率数据构建模型（训练集），预测2011年1月至2011年12月HFRS月发病率数据（测试集）。论文地址 原始数据地址

1. Wu W, Guo J, An S, et al. Comparison of Two Hybrid Models for Forecasting the Incidence of Hemorrhagic Fever with Renal Syndrome in Jiangsu Province, China. Plos One, 2015, 10(8).

图2 江苏省2004年1月至2012年12月肾综合症出血热月发病率

1. 双击打开ARIMAb.exe软件

2. 打开界面后，“数据输入”输入时间序列的数据，在excel复制粘贴即可。可以点击“原始数据绘图”显示原始数据的时间序列走势。

3. 进行平稳性检验。

      点击“原始数据”，可显示原始时间序列的平稳性检验结果（ADF检验）：检验结果一栏显示“不平稳”，同时也显示数据的周期为12，也就是呈现季节性。下方也会展示原始数据的相关图和偏相关图。

4. 根据上述的结果，个人习惯可以进行一次一般拆分（总体呈现下降趋势，当然不明显也可以不做）和一次季节性拆分（呈现出季节性分布）。

     假设只进行一次季节性拆分，不进行一般拆分，则“一般拆分（d）”输入0，“季节性性拆分（D）”输入1，再点击“一般+季节性拆分”，还是显示不平稳。

    所以进行一次季节性拆分，进行一般拆分，则“一般拆分（d）”输入1，“季节性性拆分（D）”输入1，再点击“一般+季节性拆分”，还是显示平稳。

4. 自动参数寻找

    由于上述步骤确定了拆分的数值：一次季节性拆分，进行一般拆分，所以此时d=1、D=1，填入“模型参数”的对应位置，默认勾选Log转换，点击“寻找”。

    然后开始自动寻找，寻参的流程是：

1. 首先程序自动寻找最优p、q、P、Q参数（四个参数取值均从0至3），因为传染病数据p、q、P、Q参数一般取值就是0至3；
2. p、q、P、Q参数均有统计学意义（P＜0.05）；
3. 模型的AIC值和BIC值最小。

    寻参完毕后，自动输出最优参数，比如该例子的最优模型为ARIMA（0,1,1）（3,1,1）12。

5. 模型拟合与预测

    “模型参数”输入上述输出的最优参数，“实际值输入”粘贴需要预测的实际值（本例子是江苏省2012年1月至2012年12月发病率数据），“预测数目（个）”输出12，点击“预测”。

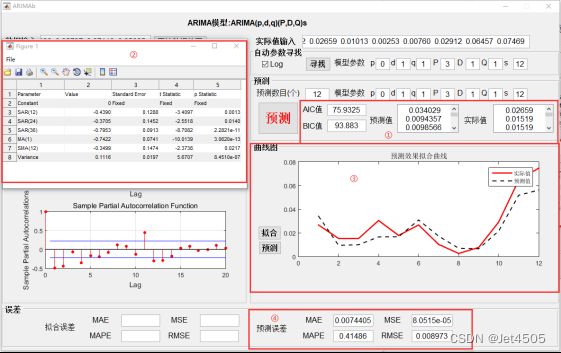
    结果显示分为四部分：

1. AIC值、BIC值，以及预测部分的预测值和实际值（提供原始数据给大家另外在其他作图软件作图用）；
2. p、q、P、Q参数的参数检验结果，可以复制粘贴另作表格；
3. 预测值和实际值曲线图展示；
4. 预测误差展示，包括MAE、MAPE、MSE、RMSE。

 

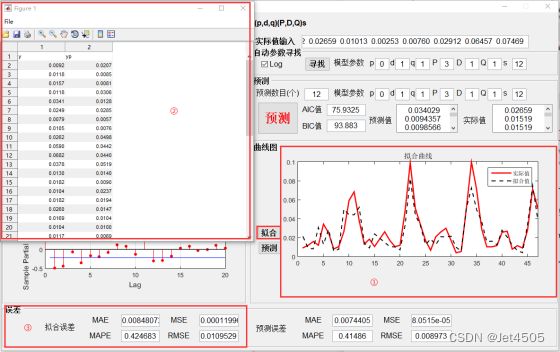
    有时候写论文也需要提供拟合的效果，因此点击“拟合”，同样显示拟合的结果：

1. 拟合值和实际值曲线图展示；
2. 提供原始数据给大家另外在其他作图软件作图用；
3. 拟合误差展示，包括MAE、MAPE、MSE、RMSE。

    可以看到，Matlab的ARIMA算法得出的最优ARIMA参数和文章得到的不太一样，这是因为每一个软件的算法差异，但是最终的性能参数是大同小异的，在论文中写清楚所使用的的软件即可。