【总结】树状数组知识点和例题详解

本博客针对树状数组进行一定的剖析并对出现的题目进行一个比较详细的总结。-ZDS

树状数组是什么？

顾名思义，树状数组是一个有着树形结构的数组，是一种数据结构。

原理其实是二进制。
基于二进制实现 我们可以知道：如果一个正整数$x$的二进制表示为$a_{k-1}{a}_{k-2}...a_2{a}_1{a}_0$
其中等于$1$的位是$a_{i_1},a_{i_2}...a_m$,则正整数的x可以被二进制分解成$x=2^{i_1}+2^{i_2}+...+2^{i_m}$
设$i_1>i_2>...>i_m$，
我们可以把它分成几个区间：
$1.$长度为$2^{i_1}$的区间$[1,2^{i_1}]$
$2.$长度为$2^{i_2}$的区间$[2^{i_1}+1,2^{i_1}+2^{i_2}]$
$3.$长度为$2^{i_3}$的区间$[2^{i_1}+2^{i_2}+1,2^{i_1}+2^{i_2}+2^{i_3}]$
…
$m.$长度为$2^{i_m}$的区间$[2^{i_1}+2^{i_2}...+2^{i_{m-1}}+1,2^{i_1}+2^{i_2}+...+2^{i_m}]$

则可以被分成$O(logx)$个区间

我们可以用$lowbit(x)$算出$[1-x]$之间的所有$O(logx)$个区间。

#define lowbit(x) (x&-x)
for(;x>0;x-=lowbit(x)){
	printf("[%d,%d]\n",x-(lowbit(x)+1,x));	
}

树状数组可以干什么？

树状数组可以解决大部分基于区间上的更新以及求和问题。

①：快速求前缀和 $O(logn)$
②：快速修改某一个数$O(logn)$
下图来自$yxc$：

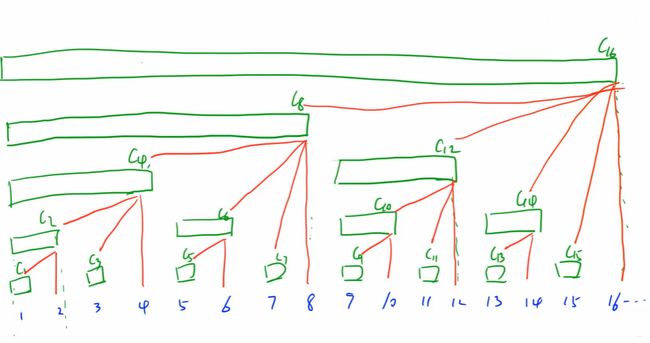
我们可以看出
$C[16]=C[8]+C[12]+C[14]+C[15]+a[16]$
$C[8]=C[7]+C[6]+C[4]+a[8]$
…

$C[2]=C[1]+a[1]$
就如同一棵树一样！我们找$C[x]$，本质上来说是找它的子节点！

我们的问题变成了，怎么求$[x-2^k+1,x-1]$的区间和$C[x]$
设$x=100..(k个)0$，$x-1=01...(k个)1$，把他们分成$k$个部分

分成四块，每一个1对应一个儿子,倒数第一个1表示长度为1的儿子，倒数第二个1表示长度为2的一个儿子…以此类推：

①$...01110...01111$
②$...01100...01110$
③$...01000...01100$
④$...00000...01000$
注意每个第一位都是不取的。因为不包含这个数，是左开右闭的区间。

用$lowbit$代码实现，$C[x]=a[x]+C[x-1]+C[x-lowbit(x-1)]+...+C[1]$每次去掉一个最后的$1$。

通过子节点找父节点–>修改操作。修改一个数，就必须找到这个数会影响到哪一个数。原理就是相当于父节点找子节点的逆运算

如$x=001111000$它的父节点一定形如$P=010000000$。

这样搞每一个点修改完之后它这些对应的值都是唯一的。

问题又来了，咋运算？

答案很明确，你$x=001111000$，加上一个$000001000$就好了呗。

那么$P=x+lowbit(x)$，我们一直找它父节点的父节点…我们找$log$次就能找到。

满足的性质：

（1）每个内部结点$C[x]$保存以它为根的子树中所有叶节点的和。
（2）每个内部结点$C[x]$的子节点个数等于$lowbit(x)$的大小
（3）除了树根之外，每个内部结点$C[x]$的父节点是$C[x+lowbit(x)]$
（4）树的深度为$O(logn)$

实现过程

求lowbit(n)

$lowbit(n)$表示取出$n(nϵN^{+})$在二进制表示下最低位的$1$以及后面的$0$构成的数组。
设$N=0$，$n$的第$k$位为$1$，第$0\to k-1$位都是$1$，再令$n=n+1$，因为进位，第$k$位变为$1$,第$0\to k-1$位变成0，在上面的取反加$1$操作之后，$n$的第$k+1$到最高位恰好与原来相反，所以n&(~n+1)仅有第$k$位为$1$，其余位都是$0$。
而在补码表示下，~n=-1-n。则lowbit=n&(-n)

long long lowbit(long long n){
	return n&(-n);
}

这么写也可以

#define lowbit(x) (x&-x)

对某个元素进行加法操作

树状数组支持单点增加。给序列中的某个数$a[x]$加上$y$，同时正确维护序列的前缀和，如上所述，只有结点$C[x]$及其所有祖先节点保存的“区间和”包含$a[x]$，而任意一个结点的祖先至多有$logN$个，逐一对他们的$C[x]$进行更新即可。
时间复杂度$O(logn)$

void add(long long x,long long y){
	for(;x<=N;x+=lowbit(x)) c[x]+=y;
}

查询前缀和

树状数组还有查询前缀和的功能。应该求出$x$的二进制表示中每个等于$1$的位，把$[1,x]$分成$O(logN)$的小区间，而每个小区间的区间和已经保存在数组$C[x]$中。

long long query(long long x){
	long long ans=0;
	for(;x;x-=lowbit(x)){
		ans+=c[x];
	}
	return ans;
}

查询[x,y]区间的值

调用上面的$query()$：$query(y)-query(x-1)$

二维树状数组

一维的树状数组是$O(logn)$的，可以扩展为$m$维，复杂度会变成$O(lo{g}^{m}n)$。扩展的的方法就是将原来的修改和查询函数中的一个循环，改成$m$个循环$m$维数组$C[x]$中的操作。
改一下操作就行。

long long add(long long x,long long y,long long z){  //将(x,y)的值加上z
	long long i=x;
	for(;i<=n;i+=lowbit(x)){
		long long j=y;
		for(;j<=m;j+=lowbit(x)){
			c[i][j]+=z;
		}
	}
}

long long query(long long x,long long y){
	long long res=0,i=x;
	for(;i>0;i-=lowbit(i)){
		long long j=y;
		for(;j<0;j-=lowbit(j)){
			res+=c[i][j];
		}
	}
	return res;
}

尤其注意

树状数组能处理的下标只有$1...n$的数组，不能出现下标为0的情况。因为$lowbit(0)=0$
会陷入死循环。

经典例题

【模板】逆序对统计

给定一个整数序列$a_1,a_2,\dots ,a_n$，如果存在$i<j$并且$a_i>a_j$，那么我们称之为逆序对。

求逆序对的数目。
输入样例：

4
3 2 3 2

输出样例：

3

分析：
定义树状数组$c[]$，$c[x]$表示在区间$[x-lowbit(x)+1,x]$的个数。

逆序访问前$n$个数（$a[n]..a[1]$） （想一想为什么逆序），对于$a[i]$，统计前缀和$sum(i-1)$，因为逆序访问，前缀和包含的数全比$a[i]$小，且在$a[i]$小，形成逆序对$sum[i-1]$个

将每次前缀和相加，就是$ans$。

访问完$a[i]$就单点增加。

数据量一大，用离散化，这里不讲。

#include
using namespace std;
long long a[1005001];
long long c[1005001];
long long n;
long long ans=0; 
long long lowbit(long long x){
	return x&-x;
}
void single_point_change(long long x,long long y){  //单点修改
	for(int i=x;i<=100010;i+=lowbit(i)){
		c[i]=c[i]+y;
	} 
}
long long interval_query(long long x){ //区间查询
	long long ans=0;
	for(int i=x;i>0;i-=lowbit(i)){
		ans=ans+c[i];
	}
	return ans;
}

int main(){
	freopen("deseq.in","r",stdin);
	freopen("deseq.out","w",stdout);
	cin>>n;
	memset(a,0,sizeof(a));
	memset(c,0,sizeof(c));
	for(int i=1;i<=n;i++){
		cin>>a[i];
	}
	for(int i=n;i>0;i--){  //思考一下为什么倒序
		ans=ans+interval_query(a[i]-1);
		single_point_change(a[i],1);
	}
	cout<<ans<<endl;
	return 0;
} 

楼兰图腾

平面上有 $N(N\le 10^5)$ 个点，每个点的横、纵坐标的范围都是 $1N$，任意两个点的横、纵坐标都不相同。
若三个点$(x1,y1),(x2,y2),(x3,y3)$满足 $x1<x2<x3,y1>y2$ 并且 $y3>y2$，则称这三个点构成"v"字图腾。

若三个点 $(x1,y1),(x2,y2),(x3,y3)$ 满足 $x1<x2<x3,y1<y2$ 并且 $y3<y2$，则称这三个点构成"^"字图腾。

求平面上"v"和"^"字图腾的个数。
输入样例：

5
1 5 3 2 4

输出样例：

3 4

分析：题目告诉我们，如果拿这$N$个点按照横坐标排序，它们的纵坐标是$1-N$的一个排列，记为$a$
$1.$类似于树状数组求逆序对，倒序扫一遍$a$，用树状数组求出$a[i]$后面有几个数比它大，记为$right[i]$
$2.$再正着扫一遍，求出每个$a[i]$前面有几个数比它大，记做$left[i]$
依次枚举每个点作为中间点，以该点为中心的“V”字图腾个数为$left[i]\ast right[i]$
则V字图腾的总数为${\sum }_{i=1}^{n}left[i]\ast right[i]$
3.按照上面的方法，我们可以统计出"^"的个数。

#include
using namespace std;
const long long N=1000200;
long long n;
long long a[1000001];
long long ans=0;
long long leftt[1000001];
long long rightt[1000001];
long long c[1000001];
long long lowbit(long long x){
	return x&-x;
}
void add(long long x,long long y){
	for(;x<=N;x+=lowbit(x)){
		c[x]=c[x]+y;
	}
}
long long ask(long long x){
	long long ans=0;
	for(;x;x-=lowbit(x)){
		ans=ans+c[x];
	}
	return ans;
}
int main(){
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i];
	for(int i=1;i<=n;i++){
		long long y=a[i];
		leftt[i]=ask(n)-ask(y);
		rightt[i]=ask(y-1);
		add(y,1);
	}
	memset(c,0,sizeof(c));
	long long ans1=0,ans2=0;
	for(int i=n;i;i--){
		long long y=a[i];
		ans1=ans1+leftt[i]*(ask(n)-ask(y));
		ans2=ans2+rightt[i]*ask(y-1);
		add(y,1);
	}
	cout<<ans1<<" "<<ans2<<endl; 
	return 0;
}