C++实现《数据结构与算法》相关算法--树与二叉树
树与二叉树相关算法实现
在数据结构与算法学习过程中,为更加深刻理解算法的实现,本文对课程中树与二叉树部分算法进行了实现。本文仅提供算法代码参考,相关算法详解请参考青岛大学王卓老师的视频课程:数据结构与算法基础(青岛大学-王卓)
目录
- 树与二叉树相关算法实现
- 二叉树相关算法
-
-
- 定义标识符
- 顺序二叉树
- 链式二叉树(带双亲结点的三叉链表)
- 定义visit方法
- 二叉树先序遍历
- 二叉树中序遍历
- 二叉树后序遍历
- 使用栈遍历二叉树(深度遍历)
-
-
- 栈的相关算法
- 非递归方法,利用栈遍历二叉树
-
- 使用队列遍历二叉树(层次遍历)
-
-
- 队列相关算法
- 利用队列遍历二叉树
-
- 构造二叉树
- 复制二叉树
- 计算二叉树深度
- 计算二叉树结点总数
- 计算二叉树叶子结点数
- 测试代码及结果
-
-
- 测试代码:
- 测试结果:
-
- 构造线索二叉树数据结构
- 构造二叉排序树数据结构
- 生成二叉排序树(三叉链表)
- 二叉排序树查找
- 二叉排序树插入
- 构造二叉排序树visit方法
- 遍历二叉排序树(输出有序序列)
- 二叉排序树的平衡调整
- 平衡二叉排序树插入
- 测试代码及结果:
-
-
- 测试代码:
- 测试结果:
-
-
- 树、森林相关算法
-
-
- 定义标识符
- 定义顺序表存储结点
- 树的存储结构(三种表示法)
-
- 哈夫曼树相关算法
-
-
- 定义标识符
- 顺序存储哈夫曼树的数据结构
- 查找权值最小的两个结点
- 创建哈夫曼树
- 顺序存储哈夫曼编码
- 构造哈夫曼编码
- 测试代码及结果
-
-
- 测试代码:
- 测试结果:
-
-
二叉树相关算法
定义标识符
// 二叉树顺序存储
#include 顺序二叉树
根据二叉树性质,完全二叉树和满二叉树比较适合采用顺序存储,此情况下树中结点的位置可以在顺序表中唯一表示。
typedef TElemType SqBiTree[MAXSIZE];
SqBiTree bt;
链式二叉树(带双亲结点的三叉链表)
二叉链表: 左、右孩子结点指针
三叉链表:左、右孩子和双亲结点指针
// 三叉叉链表存储结构
typedef struct BiNode {
TElemType data;
struct BiNode* lchild,*parent,* rchild; //左右孩子指针
}BiNode,*BiTree;
定义visit方法
可以是对结点的操作,也可以是输出结点内容
Status visit(BiTree T) {
cout << "\t" << T->data; // 根据需要定义visit功能
return OK;
}
二叉树先序遍历
根结点→左子树→右子树
// 先序遍历 :根左右
Status PreOrderTraverse(BiTree T) {
if (T == NULL)return OK;//空二叉树
else {
visit(T);//访问根结点
PreOrderTraverse(T->lchild);//递归遍历左子树
PreOrderTraverse(T->rchild);//递归遍历右子树
return OK;
}
}
二叉树中序遍历
左子树→根结点→右子树
// 中序遍历 :左根右
Status InOrderTraverse(BiTree T) {
if (T == NULL)return OK;//空二叉树
else {
InOrderTraverse(T->lchild);//递归遍历左子树
visit(T);//访问根结点
InOrderTraverse(T->rchild);//递归遍历右子树
return OK;
}
}
二叉树后序遍历
左子树→右子树→根结点
// 后序遍历 :左右根
Status PostOrderTraverse(BiTree T) {
if (T == NULL)return OK;//空二叉树
else {
PostOrderTraverse(T->lchild);//递归遍历左子树
PostOrderTraverse(T->rchild);//递归遍历右子树
visit(T);//访问根结点
return OK;
}
}
使用栈遍历二叉树(深度遍历)
栈的相关算法
typedef BiTree SElemType;
typedef struct StackNode {
SElemType data;
struct StackNode* next;
}StackNode, * LinkStack;
// 链栈的初始化
void InitStack(LinkStack& S) {
S = NULL;
}
// 判断链栈是否为空
Status StackEmpty(LinkStack S) {
if (S == NULL)return TRUE;
else return FALSE;
}
// 链栈的入栈
Status Push(LinkStack& S, SElemType e) {
LinkStack p = new StackNode; // 生成新结点p
p->data = e; // 将新结点数据域置为e
p->next = S; // 将新结点插入栈顶
S = p; // 修改栈顶指针
return OK;
}
// 链栈的出栈
Status Pop(LinkStack& S, SElemType& e) {
if (S == NULL)return ERROR;
e = S->data;
LinkStack p = S;
S = S->next;
delete p;
return OK;
}
// 取栈顶元素
SElemType GetTop(LinkStack S) {
if (S != NULL)return S->data;
}
非递归方法,利用栈遍历二叉树
// 非递归,利用栈遍历二叉树
Status SInOrderTraverse(BiTree T) {
BiTree p; // 变量初始化
BiTree q;
LinkStack S;
InitStack(S); // 栈初始化
p = T;
while (p || !StackEmpty(S)) {
if (p) {
Push(S, p);
p = p->lchild;
}
else {
Pop(S, q);
printf("%c", q->data);
p = q->rchild;
}
}
return OK;
}
使用队列遍历二叉树(层次遍历)
队列相关算法
typedef BiTree QElemType;
typedef struct {
QElemType* base; //初始化动态分配循序空间
int front; // 头指针
int rear; // 尾指针
}SqQueue;
// 队列初始化
Status InitQueue(SqQueue& Q) {
Q.base = new QElemType[MAXQSIZE]; // 分配数组空间
if (!Q.base)exit(OVERFLOW); // 内存分配失败
Q.front = Q.rear = 0; // 头指针尾指针置为0,队列为空
return OK;
}
// 求队列的长度
int QueueLength(SqQueue Q) {
return ((Q.rear - Q.front + MAXQSIZE) % MAXQSIZE);
}
// 循环队列的入队
Status EnQueue(SqQueue& Q, QElemType e) {
if ((Q.rear + 1) % MAXQSIZE == Q.front)return ERROR; // 队满
Q.base[Q.rear] = e; // 新元素加入队尾
Q.rear = (Q.rear + 1) % MAXQSIZE; // 队尾指针+1
return OK;
}
// 循环队列的出队
Status DeQueue(SqQueue& Q, QElemType& e) {
if (Q.front == Q.rear)return ERROR; // 队空
e = Q.base[Q.front]; // 保存队头元素
Q.front = (Q.front + 1) % MAXQSIZE; // 队头指针+1
return OK;
}
利用队列遍历二叉树
// 层次遍历-使用队列
// 层次遍历-使用队列
void LevelOrder(BiTree& b, string voidName) {
BiTree p;
SqQueue qu;
InitQueue(qu); // 初始化队列
EnQueue(qu, b); // 根结点指针进入队列
while (QueueLength(qu)>0) { // 队不为空,则循环
DeQueue(qu, p); // 出队结点p
visitBST(p, voidName);// 访问结点p
if (p->lchild != NULL) {
EnQueue(qu, p->lchild);// 有左孩子时将其入队
}
if (p->rchild != NULL) {
EnQueue(qu, p->rchild);// 有右孩子时将其入队
}
}
}
构造二叉树
和遍历二叉树相似(先序),相当于遍历二叉树时将visit方法改为为结点赋值。
// 构造二叉树
/*
1、从键盘输入二叉树的结点信息,建立二叉树的存储结构
2、在建立二叉树的过程中按照二叉树先序方式建立(根左右)
*/
Status CreateBiTree(BiTree &T) {
char ch;
cin>>ch;
if (ch == '#') {
T = NULL;
}
else {
if (!(T = new BiNode));
T->data = ch;//生成根结点
CreateBiTree(T->lchild); // 构造左子树
CreateBiTree(T->rchild); // 构造右子树
}
return OK;
}
复制二叉树
// 复制二叉树
int Copy(BiTree T, BiTree& NewT) {
if (T == NULL) { // 如果是空树返回0
NewT = NULL;
return 0;
}
else {
NewT = new BiNode;
NewT->data = T->data;
Copy(T->lchild, NewT->lchild);
Copy(T->rchild, NewT->rchild);
}
}
计算二叉树深度
// 计算二叉树的深度
int Depth(BiTree T) {
if (T == NULL)return 0;// 如果是空树返回0
else {
int lLength = Depth(T->lchild);
int rLength = Depth(T->rchild);
if (lLength > rLength) return(lLength + 1);
else return(rLength + 1);
}
}
计算二叉树结点总数
// 计算二叉树结点总数
int NodeCount(BiTree T) {
if (T == NULL)return 0;// 如果是空树返回0
else {
int lnum = NodeCount(T->lchild);
int rnum = NodeCount(T->rchild);
int n_num = lnum + rnum + 1;
return n_num;
}
}
计算二叉树叶子结点数
// 计算二叉树叶子结点数
int LeafCount(BiTree T) {
if (T == NULL) return 0; // 如果是空树返回0
else if (T->lchild == NULL && T->rchild == NULL) return 1; // 如果是叶子结点返回1
else return LeafCount(T->lchild) + LeafCount(T->rchild);
}
测试代码及结果
先序遍历(根左右)建立二叉树:AB##C##
A
B
C
#
#
#
#
后序遍历(左右根)访问结点结果:##B##CA
测试代码:
int main()
{
BiTree T;
CreateBiTree(T);
cout << "结点个数为: " << NodeCount(T) << endl;
cout << "叶子结点个数为: " << LeafCount(T) << endl;
cout << "树的深度为: " << Depth(T) << endl;
PostOrderTraverse(T); // 遍历二叉树 (后序遍历 :左右根)
system("pause");
return 0;
}
测试结果:
构造线索二叉树数据结构
// 线索二叉树
typedef struct BiThrNode {
int data;
int ltag,rtag;
struct BiThrNode* lchild, *rchild;
}BiThrNode,*BiThrTree;
构造二叉排序树数据结构
// 二叉排序树
typedef int KeyType;
typedef struct {
KeyType key; // 关键字
int info; // 数据域
}ElemType;
typedef struct BSTNode {
ElemType data;
struct BSTNode* lchild, * rchild; //左右孩子指针
}BSTNode, * BSTree;
生成二叉排序树(三叉链表)
// 二叉排序树生成
/*
"T" 是三叉链表结构的二叉树
"keys" 是关键字数组
"len" 是关键字数组的长度
*/
Status CreatBST(BiTree& T, KeyType keys[], int len) {
T = NULL; // 初始时树为空
int i = 0;
BiTree first_parent = NULL;
while (i < len) { // 以此将关键词插入树中
InsertBST(T, first_parent, keys[i]);
i++;
}
return OK;
}
二叉排序树查找
// 二叉排序树查找
BSTree SearchBST(BSTree T, KeyType key) {
if ((!T) || key == T->data.key) {
return T; // 若结点为空或找到指定key,则返回T
}
else if (key < T->data.key) {
return SearchBST(T->lchild, key); // 若key小于结点key值,在左子树继续查找
}
else {
return SearchBST(T->rchild, key); // 若key大于结点key值,在右子树继续查找
}
}
二叉排序树插入
// 二叉排序树插入
Status InsertBST(BiTree& T, BiTree& parent, KeyType key) {
if (T == NULL) { // 根结点为空,记录新插入的数据
if(!(T = new BiNode));
T->data.key = key;
T->lchild = NULL;
T->rchild = NULL;
T->parent = parent;
T->parent = parent;
return OK; // 插入成功
}
else if (key == T->data.key) { // 树中有相同的key,插入失败(可加入覆盖数据等操作)
return ERROR;
}
else if (key < T->data.key) { // 若小于根结点key,进入左子树
InsertBST(T->lchild,T, key); // 递归插入到左子树
}
else { // 若大于根结点key,进入右子树
InsertBST(T->rchild,T, key); // 递归插入到右子树
}
}
构造二叉排序树visit方法
- 输出关键字 “print_key”
- 计算左右子树高度差 “CHD”
- 二叉排序树平衡调整 “AdjustBBST”
// 二叉排序树结点操作方法
void visitBST(BiTree& T, string voidName) {
if (voidName == "print_key") { //访问根结点
cout << T->data.key << " ";
}
else if (voidName == "CHD") { // 计算左右子树高度差
int lheight = Depth(T->lchild);
int rheight = Depth(T->rchild);
int CHD = lheight - rheight;
T->data.info = CHD;
}
else if (voidName == "AdjustBBST") { // 二叉排序树平衡调整
int lheight = Depth(T->lchild);
int rheight = Depth(T->rchild);
int CHD = lheight - rheight;
BiTree Tlchild = T->lchild;
if (CHD > 1) {// L
int llheight = Depth(Tlchild->lchild);
int lrheight = Depth(Tlchild->rchild);
int CCHD = llheight - lrheight;
if (CCHD > 0) {// LL
cout << "LL" << "-->";
if (T->parent) { // 判断T有双亲结点
if (T->parent->lchild == T)T->parent->lchild = Tlchild; // A.parent.lchild = B
else T->parent->rchild = Tlchild; // A.parent.rchild = B
}
Tlchild->parent = T->parent; // B.parent = A.parent
T->parent = Tlchild; // A.parent = B
T->lchild = Tlchild->rchild; // A.l = B.r
Tlchild->rchild = T; // B.r = A
}// IF CCHD
else if(CCHD < 0) { // LR
cout << "LR" << "-->";
if (T->parent) { // 判断T有双亲结点
if (T->parent->lchild == T)T->parent->lchild = Tlchild->rchild; // A.parent.lchild = C
else T->parent->rchild = Tlchild->rchild;// A.parent.rchild = C
}
Tlchild->rchild->parent = T->parent; // C.parent = A.parent
T->parent = Tlchild->rchild; // A.parent = C
Tlchild->parent = Tlchild->rchild; // B.parent = C
T->lchild = Tlchild->parent->rchild; // A.l = C.r
Tlchild->parent->rchild = T;// C.r = A
Tlchild->rchild = Tlchild->parent->lchild; // B.r = C.l
Tlchild->parent->lchild = Tlchild; // C.l = B
}// IF CCHD end
}// IF CHD
else if (CHD < -1) { // R
BiTree Trchild = T->rchild;
int rlheight = Depth(Trchild->lchild);
int rrheight = Depth(Trchild->rchild);
int CCHD = rlheight - rrheight;
if (CCHD < 0) {// RR
cout << "RR" << "-->";
if (T->parent) { // 判断T有双亲结点
if (T->parent->lchild == T)T->parent->lchild = Trchild; // A.parent.lchild = B
else T->parent->rchild = Trchild; // A.parent.rchild = B
}
Trchild->parent = T->parent; // B.parent = A.parent
T->parent = Trchild; // A.parent = B
T->rchild = Trchild->lchild; // A.r = B.l
Trchild->lchild = T; // B.l = A
}// IF CCHD
else if (CCHD > 0) { // RL
cout << "RL" << "-->";
if (T->parent) { // 判断T有双亲结点
if (T->parent->lchild == T)T->parent->lchild = Trchild->lchild; // A.parent.lchild = C
else T->parent->rchild = Trchild->lchild;// A.parent.rchild = C
}
Trchild->lchild->parent = T->parent; // C.parent = A.parent
T->parent = Trchild->lchild; // A.parent = C
Trchild->parent = Trchild->lchild; // B.parent = C
T->rchild = Trchild->parent->lchild; // A.r = C.l
Trchild->lchild = Trchild->parent->rchild; // B.l = C.r
Trchild->parent->rchild = Trchild; // C.r = B
Trchild->parent->lchild = T; // C.l = A
}// IF CCHD end
}// ELSE IF CHD
else { // is balance
}// IF CHD end
}
}
遍历二叉排序树(输出有序序列)
使用中序遍历:左根右
// 二叉排序树遍历(输出有序序列)
// 中序输出:左根右
Status InOrderTraverseBST(BiTree T, string voidName) {
if (T == NULL)return OK;//空二叉树
else {
InOrderTraverseBST(T->lchild, voidName);//递归遍历左子树
visitBST(T, voidName);//访问根结点
InOrderTraverseBST(T->rchild, voidName);//递归遍历右子树
return OK;
}
}
二叉排序树的平衡调整
// 二叉树的平衡调整
/*
二叉树的平衡调整(此方法只适用于边插入边调整)
1、从根结点开始层次遍历,逐层调整二叉排序树
2、层次遍历时计算左右子树高度差
3、判断是否是完全二叉树,否则继续调整(一次调整无法完全调整)
*/
Status AdjustBBST(BiTree& T,int NodeCount) {
while(Depth(T) != ceil(log2(NodeCount + 1))) { // 判断是否是完全二叉树 h = [log2(NodeCount)+1](向上取整)
LevelOrder(T,"AdjustBBST"); // 遍历二叉排序树,并计算左右子树高度差
while(T->parent) { // 通过parent回溯,找到调整后二叉排序树的根结点
T = T->parent;
}
}
cout << endl;
return OK;
}
平衡二叉排序树插入
插入时需要检查是否破坏平衡,若破坏,则找到插入路径上离插入点最近的平衡因子的绝对值大于1的结点A,对结点A的子树进行配合调整。由于二叉排序树插入的特殊性质,插入结点必为叶子结点,因此只需要沿parent指针回溯即可找到最近的结点A。
- 插入数据元素
插入过程中计算插入路径上每个结点的左右子树高度差,由于二叉排序树必插入到叶子结点,因此路径上每个结点的高度差+1即为插入后左右子树的高度差;将绝对值大于1的结点入栈,最后出栈时即可得到结点A。
// 平衡二叉树插入(插入后找到里插入结点最近的绝对值大于1的结点)
Status InsertBBSTElem(BiTree& T, BiTree& parent, KeyType key, LinkStack &S) {
BiTree p; // 变量初始化(入栈元素)
if (T == NULL) { // 根结点为空,记录新插入的数据
if (!(T = new BiNode));
T->data.key = key;
T->lchild = NULL;
T->rchild = NULL;
T->parent = parent;
T->parent = parent;
T->data.info = 0;
return OK; // 插入成功
}
else if (key == T->data.key) { // 树中有相同的key,插入失败(可加入覆盖数据等操作)
return ERROR;
}
else if (key < T->data.key) { // 若小于根结点key,进入左子树
visitBST(T, "CHD");
T->data.info += 1;
if (abs(T->data.info) > 1) {
Push(S,T);
}
InsertBBSTElem(T->lchild, T, key, S); // 递归插入到左子树
}
else { // 若大于根结点key,进入右子树
visitBST(T, "CHD");
T->data.info += 1;
if (abs(T->data.info) > 1) {
Push(S, T);
}
InsertBBSTElem(T->rchild, T, key, S); // 递归插入到右子树
}
}
- 调整A结点的子树
Status InsertBBST(BiTree &T, KeyType key) {
BiTree parent = NULL;
LinkStack S;
InsertBBSTElem(T, parent, key, S);
Pop(S, T); // 出栈(最近的abs(CHD)大于1的Node)
AdjustBBST(T, NodeCount(T));
return OK;
测试代码及结果:
测试代码:
int main()
{
/*
BiTree T;
CreateBiTree(T);
cout << "结点个数为: " << NodeCount(T) << endl;
cout << "叶子结点个数为: " << LeafCount(T) << endl;
cout << "树的深度为: " << Depth(T) << endl;
PostOrderTraverse(T); // 遍历二叉树 (后序遍历 :左右根)
*/
BiTree BST;
int len = 5;
KeyType keys[] = {15,7,3,10,9};
cout << "--- 创建{15,7,3,10,9}的二叉排序树 ---" << endl;
CreatBST(BST, keys, len); // 创建排序二叉树
cout << "中序遍历输出排序后的keys: ";
InOrderTraverseBST(BST,"print_key"); // 中序遍历输出排序后的keys
cout << endl;
cout << "结点个数为: " << NodeCount(BST) << endl;
cout << "叶子结点个数为: " << LeafCount(BST) << endl;
cout << "树的深度为: " << Depth(BST) << endl;
cout << "---- 进行平衡调整 ----" << endl;
AdjustBBST(BST, NodeCount(BST));
cout << "平衡调整后结点个数为: " << NodeCount(BST) << endl;
cout << "平衡调整后叶子结点个数为: " << LeafCount(BST) << endl;
cout << "平衡调整后树的深度为: " << Depth(BST) << endl;
cout << "输出keys,查看是否改变排序:" << endl;
cout << "中序遍历输出排序后的keys: ";
InOrderTraverseBST(BST, "print_key"); // 中序遍历输出排序后的keys
cout << endl;
cout << "---- 插入元素 ----" << endl;
int insert_key = 8;
InsertBBST(BST, insert_key);
cout << "插入并调整后结点个数为: " << NodeCount(BST) << endl;
cout << "插入并调整后叶子结点个数为: " << LeafCount(BST) << endl;
cout << "插入并调整后树的深度为: " << Depth(BST) << endl;
cout << "中序遍历输出排序后的keys: ";
InOrderTraverseBST(BST, "print_key"); // 中序遍历输出排序后的keys
system("pause");
return 0;
}
测试结果:
树、森林相关算法
定义标识符
// 树存储结构
#include 定义顺序表存储结点
typedef TElemType SqBiTree[MAXSIZE];
树的存储结构(三种表示法)
- 双亲表示法
/*
双亲表示法
*/
// 结点结构
typedef struct PTNode {
TElemType data;
int parent; // 双亲位置域
}PTNode;
// 树结构
typedef struct {
PTNode nodes[MAX_TREE_SIZE];
int r, n; // 根节点的位置和结点的个数
}PTree;
- 孩子表示法
/*
孩子表示法
*/
// 孩子结点结构
typedef struct CTNode {
int child;
struct CTNode* next;
}*ChildPtr;
// 双亲结点结构
typedef struct {
TElemType data;
ChildPtr firstchild; // 孩子链表头指针
}CTBox;
// 树结构
typedef struct {
CTBox nodes[MAX_TREE_SIZE];
int n, r; // 结点数和根结点的位置
}CTree;
- 孩子兄弟表示法
用二叉树结构表示树,由于二叉树拥有许多方便的性质,这种表示法可以把树转换为二叉树。
// 孩子兄弟结构
typedef struct CSNode {
TElemType data;
struct CSNode* firstchild, * nextsibling;
}CSNode,*CSTree;
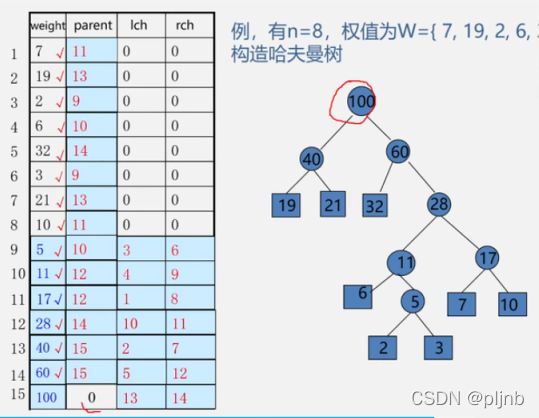
哈夫曼树相关算法
定义标识符
// 哈夫曼树的构造
#include 顺序存储哈夫曼树的数据结构
typedef struct {
double weight; // 双亲结点到本结点路径的权值
char data; // 数据域
int parent, lch, rch; // 子树、双亲结点的位置
}HTNode,*HuffmanTree;
查找权值最小的两个结点
Status Select(HuffmanTree HT, int n, int& s1, int& s2) {
double min_weigth1 = 999999;
double min_weigth2 = 999999;
for (int i = 1; i <= n; i++) {
double weight1 = HT[i].weight;
if (HT[i].weight < min_weigth1 && HT[i].parent == 0) {
min_weigth1 = weight1;
s1 = i;
//cout << "min weight1 = " << min_weigth1 << endl;
}
}
for (int i = 1; i <= n; i++) {
double weight2 = HT[i].weight;
if (weight2 < min_weigth2 && i != s1 && HT[i].parent == 0) {
min_weigth2 = weight2;
s2 = i;
//cout << "min weight2 = " << min_weigth2 << endl;
}
}
return OK;
}
创建哈夫曼树
void CreatHuffmanTree(HuffmanTree &HT, int n) { // 构造哈夫曼树 --- 哈夫曼算法
if (n <= 1)return;
int m = 2 * n - 1; // 数组共有2n-1个元素
HT = new HTNode[m + 1]; // 0号单元未用,HT[m]表示根结点
for (int i = 1; i <= m; ++i) { // 将2n-1个元素的lch、rch、parent置为0
HT[i].lch = 0;
HT[i].rch = 0;
HT[i].parent = 0;
}
for (int i = 1; i <= n; ++i) {
cout << "请输入第" << i << "个元素" << endl;
cin >> HT[i].data;
cout << "其权值为: " << endl;
cin >> HT[i].weight;// 输入前n个元素的weight值
}
// 初始化结束,下面开始建立哈夫曼树
for (int i = n + 1; i <= m; i++) {
int s1 = 1;
int s2 = 1;
Select(HT, i - 1,s1, s2); // 在HT[k](1≤k≤i-1)中选择两个其双亲域为0,
// 且权值最小的结点,并返回他们在HT中的序号s1和s2
HT[s1].parent = i;
HT[s2].parent = i; // 表示从F中删除s1,s2
HT[i].weight = HT[s1].weight + HT[s2].weight;
// i的权值为左右孩子权值之和
HT[i].lch = s2;
HT[i].rch = s1;
//cout << HT[i].weight << "\t" << HT[s1].weight << "\t" << HT[s2].weight << endl;
}
}
顺序存储哈夫曼编码
typedef struct{
char data; // 数据域
char *code; // 编码域
}HCode, *HuffmanCode;
构造哈夫曼编码
void CreatHuffmanCode(HuffmanTree HT, HuffmanCode& HC, int n) {
// 从叶子到根逆向求每个字符的哈夫曼编码,存储在编码表HC中
HC = new HCode[n + 1]; // 分配n个字符编码的头指针矢量
char *cd;
cd = new char [n]; // 分配临时存放编码的动态数组空间
cd[n - 1] = '\0'; // 编码结束符
for (int i = 1; i <= n; ++i) {
int start = n - 1;
int c = i;
int f = HT[i].parent;
while (f != 0) { // 从叶子结点开始向上回溯,直到根结点
--start; // 回溯以此start向前指一个位置
if (HT[f].lch == c) cd[start] = '0'; // 结点c是f的左孩子,则生成代码0
else cd[start] = '1'; // 结点c是f的右孩子,则生成代码1
c = f;
f = HT[f].parent; // 继续向上回溯
}
HC[i].code = new char[n - start]; // 为第i个字符串编码分配空间
HC[i].data = HT[i].data;
strcpy_s(HC[i].code, n - start, &cd[start]); // 将求得的编码从临时空间cd复制到HC的当前行中
}
delete cd; // 释放临时空间
}
测试代码及结果
测试代码:
int main()
{
int n;
cout << "输入字符数量:";
cin >> n;
HuffmanTree HT;
HuffmanCode HC;
CreatHuffmanTree(HT, n);
CreatHuffmanCode(HT, HC, n);
for (int i = 1; i <= 2 * n - 1; i++) {
cout << "序号为:" << i << " 的权值为:" << HT[i].weight << "\tparent: " << HT[i].parent << "\tlch: " << HT[i].lch << "\trch: " << HT[i].rch << endl;
}
for (int i = 1; i <= n; i++) {
cout << "序号为:" << i << " 的字符为:" << HC[i].data << "\t编码为:"<< HC[i].code << endl;
}
system("pause");
return 0;
}