二叉树结构与算法思路解析

二叉树

介绍

主要内容

• 二叉树的概念和性质
• 二叉树的存储结构
• 遍历二叉树
  • 递归遍历
  • 非递归遍历
• 线索二叉树
• 哈夫曼树
• 树和森林
  • 树和森林的存储
  • 树和森林与二叉树的转换
  • 树和森林的遍历

树型结构特点

一对多

例：

• 自然界，树
• 人类社会，家谱，新政组织结构
• 计算机领域
  • 操作系统的文件组织结构
  • 基于26个字母索引的查找树等
  • 编译原理中表达式求值操作等

一：树和二叉树的基本概念

1. 树的定义

   树是n(n>=0)个结点的有限集合，在任一棵非空树中：

   • 有且仅有一个称为根的结点；
   • 其余结点可以分为多个互不相交的集合，而且这些集合中的每一集合都是本身又是一棵树，称为根的子树-----递归定义

2. 树的基本术语

   • 结点：树中的元素，包含一个数据元素及若干指向子树的分支
   • 结点的度：结点拥有的子树的个数
   • 结点层：从根结点开始算起，根为第一层；根的孩子为第2层结点；…
   • 孩子：结点的子树的根称为该结点的孩子
   • 双亲：孩子结点的上层结点，称为这些结点的双亲
   • 兄弟： 同一双亲的孩子结点
   • 树的高度：树中最大的结点层
   • 树的度：树中最大的结点度
   • 叶子：也叫终端结点，是度为0的结点
   • 分支结点：度不为0的结点
   • 森林：互不相交的树集合
   • 有序树：子树有序的树，如家族树
   • 无序树：不考虑子树顺序的树

3. 二叉树的概念

   二叉树定义： 二叉树是有限元素的集合，该集合或为空，或由一个称为根的元素及两个不相交、分别称为左子树和右子树的二叉树构成；左，右子树本身也是二叉树------递归定义。二叉树结点的度可以为0，1，或2，最大为2。

   二叉树优点：

   • 二叉树结构简单，规律性强
   • 所有的树都可以转换成唯一对应的二叉树

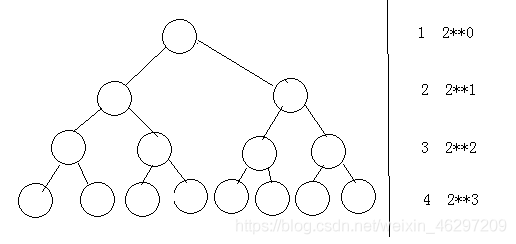
   满二叉树：如果深度为k的二叉树有2^k -1 个结点，则称为满二叉树。特点：每一层上都含有最大结点数

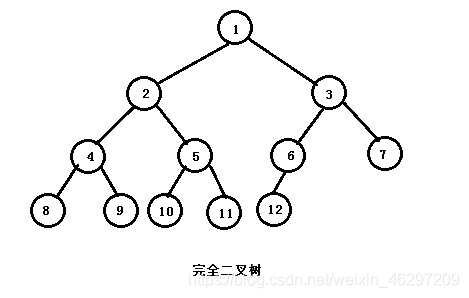
   完全二叉树：如果二叉树除最后一层外每一层都是满的，且最后一层或者是满的，或者结点都连续地集中在该层的最左端，则称其为完全二叉树。特点：所有的叶子结点都出现在第k层或k-1层。如下图所示：

   

   满二叉树一定是完全二叉树

4. 二叉树特点

   • 二叉树中每个结点最多有两棵子树，二叉树每个结点度小于等于2
   • 二叉树是有序树：二叉树结点的子树要区分左子树和右子树，即使只有一棵子树也要进行区分，说明它是左子树还是右子树。

   注意：对于树来说，如果只有一个孩子，没有左右之分

   例：对于树和二叉树，如果有三个结点分别有哪几种形态？

5. 二叉树性质

   • 性质1：对于非空二叉树，如果叶子结点数为n₀，度为2的结点数为n₂，则有n₀ = n₂ + 1

     证明：

     ​ 设二叉树中度为1的结点数为n1，二叉树中的总结点数为N，因为二叉树中所有结点均小于或等于2，所有有：

     ​ N = n₀ + n₁ + n₂ (1式)

     ​ 再看二叉树中的分支数，处根结点外，其余结点都由一个分支与其双亲相连接，设B为二叉树中的分支总数，则有：

     ​ N = B + 1 (2式)

     ​ 由于这些分支都是由度为1和2的结点射出，所以有：

     ​ B = n₁ + 2 * n₂ (3式)

     即：N = B + 1 = n₁ + 2 * n₂ + 1 (4式)

     结合1式和4式可得：n₀ + n₁ + n₂ = n₁ + 2 x*n₂ + 1

     即：n₀ = n₂ + 1

   • 性质2：一棵非空二叉树的第i层上最多有2^(i-1)个结点(i>=1)

• 性质3：一棵深度为k的二叉树中，最多有2^k-1个结点（k>=1）

  证明：深度为k的二叉树取最多结点时，二叉树中的每层上均应取最多结点。根据性质2得到，每层上的最大结点数为2^(i-1)，则二叉树中的总结点数为：2⁰ + 2¹ + … + 2^(k-1) = 2^k -1

• 性质4：具有n个结点的完全二叉树的深度为：【log₂n】+ 1。（这里【x】表示对x向下取整）

  证明：假设此二叉树的深度为k，则根据性质3及完全二叉树的定义得到：2^(k-1) <= n <= 2^k -1

  两边取对数得到：k-1 <= log₂n < k

  因为k是整数，所以k = 【log₂n】 + 1

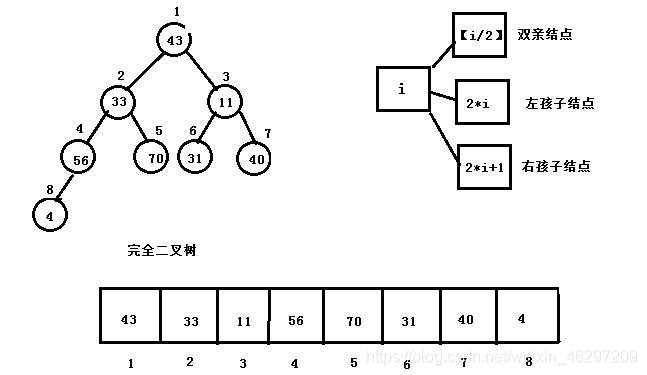
• 性质5：如果一棵有n个结点的完全二叉树的结点按层序编号(从第1层到第【log₂n】+1 层，每层从左到右)，则对任一结点i(1<=i<=n)：

  • 如果i=1，则结点i是二叉树的根，无双亲；如果i>1，则 其双亲是结点【i/2】

  • 如果2i<=n，则其左孩子是结点2i；否则i无左孩子，为叶子结点

  • 如果2i+1<=n，则其右孩子是结点2i+1；否则结点i无右孩子

二：二叉树的顺序存储

二叉树的顺序存储一般是按照从上至下、从左至右的顺序存储。但是，这样存储后结点在存储位置上的前驱、后继关系并不是他们在逻辑上的邻接关系，只有通过一些方法能够确定结点在逻辑上的前驱和后继结点，这种存储才有意义。

1. 完全二叉树的顺序存储

   完全二叉树按照这种编号方式时，依据性质5，树中结点的序号可以唯一地反映出结点之间的逻辑关系，这样既能够最大可能地节省存储空间，又可以利用列表元素的下标值确定结点在二叉树中的位置以及结点之间的关系。所以完全二叉树适合于采用顺序存储方式。

   图解：

解析：

我们开辟一块连续的内存空间，将完全二叉树的的结点存放到连续的内存空间中去，依据性质5就使得这个连续的内存空间具有了逻辑性。

2. 一般二叉树的顺序存储

   对于一般二叉树，只有按完全二叉树的形式增添一些并不存在的空结点，才能利用性质5使用顺序存储的方式

   图解：

解析：

​ 先将一般二叉树补全为完全二叉树，没有的部分以一个空结点补全。然后在内存中开辟一块足够大的连续空间。将二叉树的值填入到内存空间中，空结点以0来表示。空间的大小为最后一个结点所在的下标的值。

3. 总结

   ​ 这种存储方式会造成空间的大量浪费，最坏的情况是单支树，一棵深度为k的右单支树，只有k个结点，却需要分配2^k-1个存储单元。

   优点：结点之间的关系蕴含在其存储中。

   缺点：浪费空间。只适合用来存放完全二叉树。

三：二叉树的链式存储

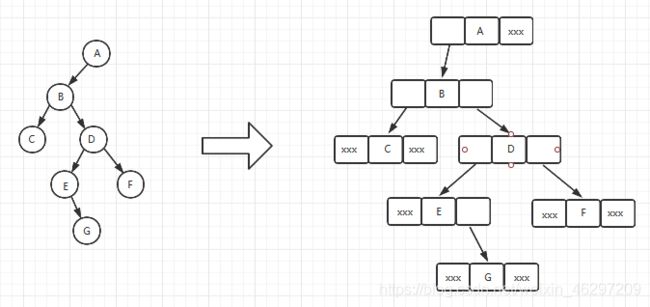
1. 二叉链表

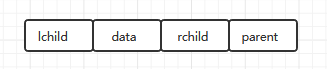
   链表中每个结点包含三个域，数据域和两个指针域，指针域分别用来指示该结点的左孩子和右孩子所在的结点的存储地址。

   结点的存储结构为：

在n个结点的二叉链表中，有 n+ 1 个空指针域

二叉链表内存结构图解(xxx为空指针域)：

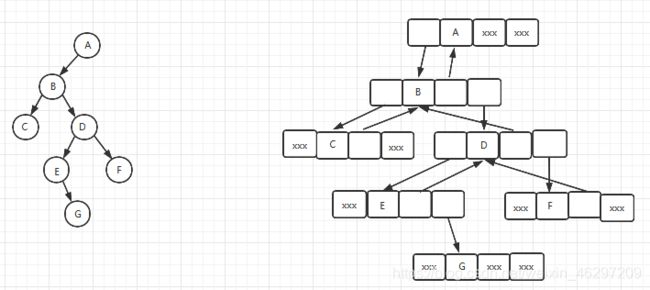
2. 三叉链表

   三叉链表中每个结点由4个域组成：数据域、双亲指针域、左指针域、右指针域。双亲域为指向该结点双亲结点的指针。

   存储结构为：

三叉链表既便于查找孩子结点，又便于查找双亲结点；但是，相对于二叉链表而言它增加了空间的开销。故二叉链表是最常用的二叉树存储方式，以下的遍历，查询操作都是针对二叉链表进行的。

三叉链表内存结构图解

3. 遍历二叉树

​ 二叉树的遍历是按一定次序对二叉树中的每个结点做逐一访问，或查找具有某个特点的结点，然后对这些满足条件的结点进行处理。例如：求叶子结点个数，对每个结点值做一下修改，打印所有结点等等。

​ 由二叉树的定义可知，一棵二叉树是由根结点、根结点的左子树、根结点的右子树三部分组成。因此，只要依次遍历这三部分，就可以遍历整个二叉树。

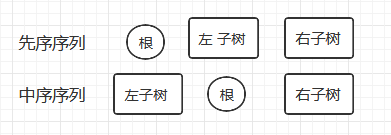
​ 二叉树的遍历可以理解为：访问根，遍历左子树和遍历右子树。令L为遍历左子树，D为访问根结点，R为遍历右子树。对L,D,R进行排列共有6种排列顺序(自行排列)，约定先左后右则有三种遍历方法：DLR，LDR，LRD，分别称为先序遍历、中序遍历、后序遍历。

• 先序遍历

  若二叉树为空，遍历结束。否则：

  • 访问根结点
  • 先序遍历根结点的左子树
  • 先序遍历根结点的右子树

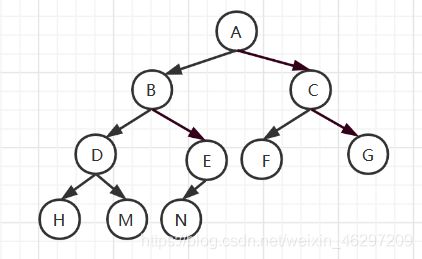
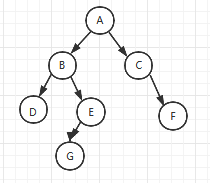
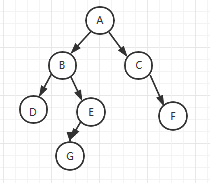
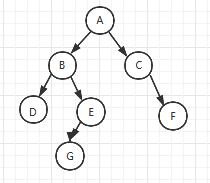
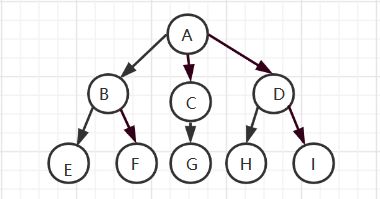
  如下图所示二叉树的先序遍历结果为：A B D E G C F

• 中序遍历

  若二叉树为空，遍历结束。否则：

  • 中序遍历根结点的左子树
  • 访问根结点
  • 中序遍历根结点的右子树

  如下图所示二叉树的中序遍历结果为：D B G E A C F

• 后序遍历

  若二叉树为空，遍历结束。否则：

  • 后序遍历根结点的左子树
  • 后序遍历根结点的右子树
  • 访问根结点

  如下图所示二叉树的后序遍历结果为：D G E B F C A

• 扩展：

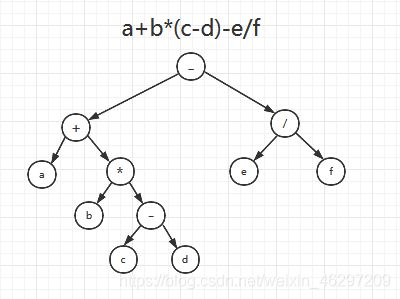
  用二叉树表示表达式：a+b*(c-d)-e/f （中缀表达式），我们平时在数学中见到的表达式都是以中缀表达式来定义的。上述表达式可用以下二叉树表示。

我们在看的时候从左下对应着表达式的计算顺序开始看起。

我们将上面的二叉树以先序遍历和后序遍历来显示表达式如下：

• 先序序列：-+a*b-cd/ef

  前缀表达式(波兰式)：前缀表达式的运算符位于操作数之前

• 后序遍历：abcd-*+ef/-

  后缀表达式(逆波兰式)：后缀表达式的运算符位于操作数之后

我们平时读一个表达式是以中缀表达式的方式来读的，但计算机无法识别中缀表达式的运算，需要先将中缀表达式转换为前缀表达式或后缀表达式，然后计算机才能够进行运算。

4. 由遍历序列恢复二叉树

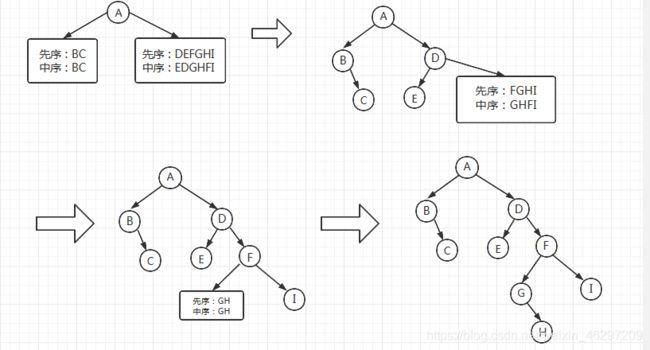
​ 任意一棵二叉树的先序序列和中序序列都是唯一的，如果已知结点的先序序列和中序序列，则可以唯一的确定这棵二叉树。如图所示：

​ 先序序列先遍历根，所以由二叉树先序序列的第一个结点确定树/子树的树根

​ 由得到的树根将中序序列分为左子树中序序列和右子树中序序列

​ 将左右子树按相同的方法进行恢复

​ 例：已知一棵二叉树的先序序列和中序序列分别为：

​ 先序序列：ABCDEFGHI

​ 中序序列：BCAEDGHFI

​ 恢复二叉树的过程如下图所示：

​

​ 通过恢复的二叉树我们可以得到它的后序序列为：CBEHGIFDA

​ 恢复二叉树的两个序列中必须有中序遍历序列来区分左子树序列和右子树序列，所以用两种序列恢复二叉树一共有两种方案：先序序列和中序序列恢复，后序序列和中序序列恢复。

​ 扩展：二叉树除了我们上面讲的三种序列外，还有一种序列叫层次遍历，即按从上到下，从左到右顺序遍历。

5. 二叉树的遍历算法递归实现方式

因为我们目前还没有创建二叉树(创建二叉树在下一篇会讲到)，所以我们在这里先讲一下它的实现思想，不涉及具体代码。以下代码仅供了解算法实现思想。

先序遍历算法：

def preorder(t):
	if t == None:
		return None
	print(t.data)
	preorder(t.lchild)
	preorder(t.rchild)

中序排列算法：

def midtraverse(t):
	if t == None:
		return None
	midtraverse(t.lchild)
	print(t.data)
	midtraverse(t.rchild)

后序排列算法

def postorder(t):
	if t == None:
		return None
	postorder(t.lchild)
	postorder(t.rchild )
	print(t.data)

我们可以看到，三种遍历算法的不同仅在于递归调用顺序的不同。

6. 遍历算法的应用

统计二叉树中叶子结点的个数

如何判断叶子结点(二叉链表)：

​ 当一个结点的左孩子和右孩子即左指针域和右指针域为空的时候，这个结点就是叶子结点。

如何找到叶子结点：

​ 定义一个计数器，然后遍历二叉树的每一个元素，遍历方式可以为先序、中序、后序任意一种。如果这个元素的左右指针域都为空时，则让计数器加1，直至遍历完所有结点。

注：因为我们在遍历时进行的是递归操作，需要在每一个函数中进行累加，所以计数器需设置为全局变量。

def countleaf(t):
	if t == None:
		return None
	if t.lchild == None and t.rchild == None:
		global n  # 全局变量
		n = n+1  # 叶子数n累加
	countleaf(t.lchild)
	countleaf(t.rchild)

7. 建立二叉树二叉链表存储结构

​ 在以上的遍历等操作中，我们都是在二叉链表已经建立好的情况下进行的，但事实上我们并没有建立一个二叉链表，接下来我们就讲一下如何建立二叉链表。

​ 基本思想：设每个元素是一个字符。输入先序序列(在空字符串添加*)，按先序遍历的顺序，建立二叉链表的所有结点并完成相应结点的链接。

​ 在遍历过程生成结点，建立二叉树的链式存储结构，需按先序遍历算法建立二叉树的存储结构，先建立根，再建立根的左右子树。

​ 注：在建立二叉树的过程中，只能依赖于先序遍历进行创建

定义结点类

class Node:
	def __init__(self,data=None,lchild=None,rchild=None):
		self.data = t
		self.lchild = lchild
		self.rchild = rchild

定义二叉树创建函数

# 先序递归遍历二叉树
def creatBT(self):
    ch = input("请从键盘上输入一个字符")
    if ch == "*":
    	T = None
    else:
        T = Node()
        T.data = ch
        T.lchild = creatBT()  # 建立左子树
        T.rchild = creatBT()  # 建立右子树
    return T  # 返回根结点

三：二叉树的列表存储

为什么可以使用列表来存放二叉树？

• 二叉树是递归定义的
• python的列表也是递归结构

步骤：

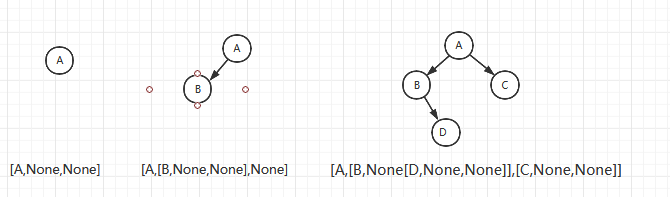
• 空数用None表示
• 非空二叉树用包含三个元素的列表[data,lchild,rchild]表示

把一棵二叉树映射到一种分层的list结构，每棵二叉树都有与之对应的列表。结构如图所示：

创建一个二叉树列表结构

初始化一个二叉树结点

# 创建二叉树结点类
class BinTreeList:
	def __init__(self,data,lchild=None,rchild=None):
		# 初始化一个结点
		self.btree = [data,lchild,rchild]
# 创建一个类对象
t = BinTreeList("A")

当我们实例化一个二叉树结点对象后，这个对象就是一个包含三个元素的列表，即为[“A”,None,None]

判断结点是否为空

def is_empty_bintree(self):
	return self.btree[0] is None

设置左孩子

def set_lchild(self,lchild):
	if self.is_empty_bintree():
		print("tree is empty")
	# 左右孩子同样为一个列表，需要用btree方法将列表取出来
	self.btree[1] = lchild.btree  

设置右孩子

def set_rchild(self,rchild):
	if self.is_empty_bintree():
		print("tree is empty")
	self.btree[2] = rchild.btree

递归遍历二叉树

先序遍历

def preorder(t):
	if t == None:
		return None
	print(t[0])
	preorder(t[1])
	preorder(t[2])

中序遍历

def preorder(t):
	if t == None:
		return None
	preorder(t[1])
	print(t[0])
	preorder(t[2])

后序遍历

def preorder(t):
	if t == None:
		return None
	preorder(t[1])
	preorder(t[2])
	print(t[0])

求二叉树中叶子结点个数

def leafnum(t):
	if t == None:
		return None
	if t[1] == None and t[2] == None:
		global n
		n = n + 1
	else:
		leafnum(t[1])
		leafnum(t[2])

查找某个元素

def searchdata(t,data):
	if t == None:
		return None
	if t[0] = data
		retrun 1
	else:
		searchdata(t[1],data)
		searchdata(t[2],data)

总结：

• 列表是python的一种标准类型，二叉树结点是一个三元组
• 二叉树是递归结构，python的列表也是递归结构
• python的元组也可以实现这种二叉树的递归结构，但是实现的是非变动性二叉树结构，因为元组是不可变类型。

四：二叉树遍历的非递归算法

​ 由先序、中序、后序的遍历过程及代码可知，先序、中序、后序遍历过程中经过结点的路线是相同的，只是输出的时机不同。

​ 路线的形成：它们都是先从根结点开始，沿左子树深入，去判断左子树是否存在，如果存在则进一步判断，直至到达最低端。然后从最低端返回到相应的根结点处，从根结点处再判断右子树是否存在，直到最后从根结点的右子树返回到根结点。

​ 先序遍历：遇到结点就打印

​ 中序遍历：从左子树返回时遇到结点访问

​ 后序遍历：从右子树返回时遇到结点访问

​ 返回结点的顺序与深入结点的顺序相反，即后深入先返回，所以可以利用栈辅助实现遍历

​ 基本思想：

• 在沿左子树深入时，深入一个结点压栈一个结点
• 若为先序遍历，则在入栈前访问
• 当沿左分支深入不下去时则返回，即从堆栈中弹出刚压栈的结点，若为中序遍历，则此时访问该结点，然后从该结点的右子树继续深入
• 若为后序遍历，则将此结点再次入栈，然后从该结点的右子树继续深入…直到第二次从栈里弹出该结点，即从右子树返回时，才访问之。

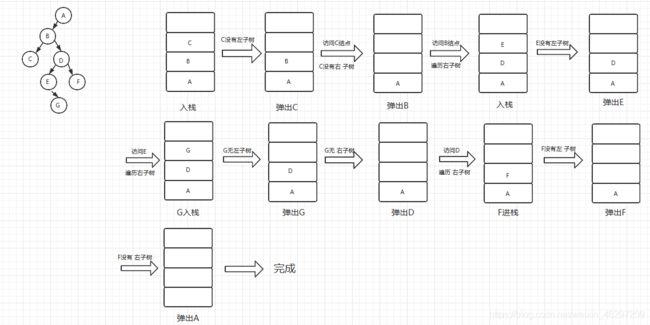
我们以非递归中序遍历为例：

图解：

规律：

• 只要栈中弹出了一个元素，下一步就是访问这个元素，即进入这个元素的右子树中
• 当一个元素没有左子树时，就会将这个元素弹出并访问
• 当一个元素没有右子树树时，就会将此时栈中最上面的元素弹出并访问

代码实现：

​ 关于栈的创建代码在以前的博客中有过详细介绍，这里不再复写。这里优先了解代码思路。

​ t最先指向根结点

def InOrder(t):
	p = t
	s = ListStack()  # 初始化一个栈
	while s.is_empty() != 1 or p != None:  # 如果栈或p不为空
		while p != None:  # 如果p不为空
			s.pushstack()  # 将当前节点入栈
			p = p.lchild  # 向左子树不断深入
			
		if not s.is_empty():
			p = s.popstack()  # 弹出栈顶元素，并将弹出元素赋值给p，相当于返回到当前树的根结点
			print(data)  # 打印当前节点元素
			p = p.rchild  # 遍历右子树

五：哈夫曼树

1. 哈弗曼树的用途

   ​ 哈弗曼树是一种重要的二叉树，又称"最优树"，或者"最优二叉树"，在信息领域中有重要的理论和实际价值

2. 哈夫曼树的定义

   • 路径：从一个祖先结点到子孙结点之间的分支构成这两个结点间的路径；

   • 路径长度：路径分支上的分支数目称为路径长度

   • 结点的权：在许多应用中，常常将树中的结点赋上一个有着某种意义的实数，称此实数为该结点的权。

   • 结点的带权路径长度：从根到该结点的路径长度与该结点权的乘积

   • 树的带权路径长度=树中所有叶子结点的带权路径之和，通常记作：
     $$WPL=\sum _{i=1}^n{w}_i\ast l_i$$
     w_i为权值，l_i为根到结点的路径长度

   哈夫曼树：假设有n个权值(w₁,w₂,…,w_n)，构造有n个叶子结点的二叉树，每个叶子有一个w_i作为它的权值。则带权路径长度最小的二叉树称为哈夫曼树。

3. 哈夫曼树图解

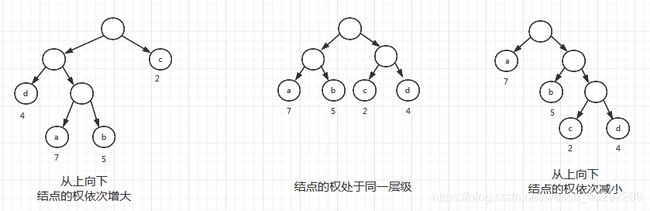
   例：有4个结点，权值分别为7,5,2,4，构造有4个叶子结点a,b,c,d分别对应4个权值的二叉树

第一棵树的WPL为：
$$2\ast 4+3\ast 7+3\ast 5+2=46$$
第二棵树的WPL为：
$$2\ast 7+2\ast 5+2\ast 2+2\ast 4=36$$
第三棵树的WPL为：
$$7+2\ast 5+3\ast 2+3\ast 4=35$$
第三棵树的WPL最小，我们将类似于第三课树的二叉树称之为哈夫曼树

哈夫曼树特征：权值越大的叶子越靠近树根，权值越小的叶子越远离树根

4. 哈夫曼树构建步骤

   将n个权值{w₁,w₂,…,w_n}对应n个结点，构成具有n棵二叉树的森林F={T₁,T₂…T_n}，其中每棵二叉树T_i(1<= i <=n)都只有一个权值为w_i的根结点，其左，右子树均为空

   • 在森林F中选出两棵根结点的权值最小的树作为一棵新树的左、右子树，且新树的根结点的权值为其左、右子树上根结点的权值之和
   • 从F中删除构成新树的那两棵树，同时把新树加入F中
   • 重复2和3步，直到F中只含有一棵树为止，此树便是哈夫曼树

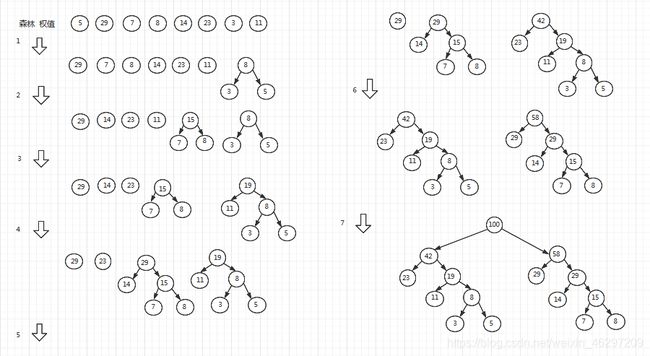
   例：利用w={5, 29, 7, 8, 14, 23, 3, 11}构建一棵哈夫曼树，详细创建过程如下图所示

注：哈夫曼树的结构不唯一，当我们在将两棵树合成一棵新树的时候，在没有约定的情况下不区分左右子树，所以哈夫曼树的结构不唯一。哈夫曼树虽然不唯一，但WPL是唯一的。

5. 哈夫曼树构建算法

   • 哈夫曼树的存储结构

   

   • 算法思路

     • 将n个叶子结点的数据存放到列表中
     • 对列表进行排序，找列表中两个权值最小的结点分别作为左右子树，创建一个新的树，新树的根的权值为左右两个子树权值之和，并修改这三个结点的指针指向；父结点的左右指针分别指向左右孩子，孩子结点的父指针指向父结点。
     • 把刚才的两个权值最小的结点从列表中删除，并把新的根结点加入到列表中
     • 重复2，3步骤，直到列表中只有一个元素为止，即只有根结点。

   • 算法描述

     例：构造以{7, 5 , 2, 4}为权值的哈弗曼树

   # 定义节点类
   class Node:
   	def __init__(self,data):
            self.lchild = None
            self.rchild = None
            self.parent = None
            self.data = data
   	def makeTree(self,nodes):
        nodes_list = nodes[:]
        while len(node_list) > 1:
        # 将列表进行排序
        nodes_list.sort(key = lambda item:item.data)
        # 取出最小的元素作为左子树值并将这个值删除
        node_left = nodes_list.pop(0)
        # 取出第二小的元素作为右子树值并将这个值删除
        nonde_right = nodes_list.pop(0)
        # 创建父结点，父结点的值为左右子树值的和
        node = Node(node_left + node_right)
        # 将父结点的左指针指向左子树
        node.lchild = node_left
        # 将父结点的右指针指向右子树
        node.rchild = node_right
        # 将左子树的父指针指向父结点
        node_right.parent = node
        # 将右子树的父指针指向父结点
        node_left.parent = node
        # 把新生的树加入到列表中
        nodes_list.append(node)
        # 最后一个元素是根节点，没有父结点
        nodes_list[0].parent = None
        # 返回根结点
        return nodes_list[0]
   

6. 哈夫曼编码

   ​ 哈夫曼编码(Huffman Coding)，又称霍夫曼编码，是一种编码方式，可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法，该方法完全依据字符出现概率来构造异字头的平均长度最短的码字，有时称之为最佳编码，一般就叫做Huffman编码(有时也称为霍夫曼编码)

   ​ 编码：在数据通信中，需要对传送的文字转化为二进制字符0，1组成的二进制串

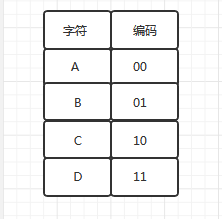
   ​ 例如：设要发送电文"ABACCDA"，其中只含有4种字符A，B，C，D

   • 等长编码

     编码二进制位数与字符的个数有关。以下图等长编码对电文进行编码后为：00010010101100

   

   • 不等长编码

     将出现次数多的字符用较短的二级制位进行编码。以下图不等长编码对电文进行编码后位：010011010

   

   此方案中当我们在对代码串进行译码时，会出现AC=D的情况，这是因为字符A的编码是字符D编码的前缀，具有二义性。

   最优编码要求：

   • 采用不等长编码，使报文尽量短

   • 任何一个字符的编码都不能是其它字符编码的前缀，保证译码的惟一性。

   解决方案：

   • 统计字符集中每个字符在电文中出现的概率，概率越大编码越短。
   • 利用哈夫曼树的特点，权越大的叶子离根越近，将每个概率值作为权值，构造哈夫曼树。则概率越大的结点，路径越短。
   • 在哈夫曼树的每个结点的左分支标0，右分支标1
   • 从根到每个叶子的路径上标号链接起来，作为该叶子代表的字符的编码

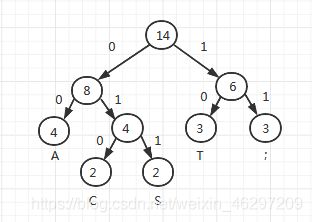
   例：设要传输额字符集D={C, A, S, T, ;}，字符出现频率w={2, 4, 2, 3, 3}

   • 通过字符出现的频率即权值确定哈夫曼树

   

   由上述哈夫曼图可得各个字符的编码：

   A：00 C：010 S：011 T：10 ;：11

   我们可以看出，哈夫曼编码完全契合编码要求

   哈夫曼编码总长最短原因：因为哈夫曼树的带权路径长度最短，即每个字符的编码长度与其出现的次数或频度的乘积之和最短，也就是电文的编码总长最短。

   哈夫曼树保证译码唯一性原因：因为在哈夫曼树中，每个字符结点都是叶子结点，它们不可能在根结点到其它字符结点的路径上。

   算法实现：

   在哈夫曼树的三叉链表结构中，从各个叶子结点开始，沿叶子结点的双亲链域退到根结点，在回退的过程中，根据分支的左右确定编码。

   注：由于一个字符的哈夫曼编码是从根结点到相应叶子结点所经过的路径上各分支组成的0，1序列，因此先得到的分支代码应为所求编码的低位码。

   过程：

   • 遍历nodelist，从第一个叶子结点开始回退
   • 遇到左分支设置为0，遇到右分支设置为1
   • 直到回退到根结点，再去找下一个叶子结点

   叶子结点图解：

代码实现：

nodes为一个保存有叶子结点的列表

def hufumanCode(nodes,root):
	# 初始code_list列表长度，列表长度即为叶子结点的个数
	code_list = [""] * len(nodes)
	# 对每个列表中每个结点进行求编码
    for i in range(len(nodes)):
    	# 判断当前节点是否是root结点
        while node[i] != root:
            # 判断是否有左子树
            if node[i].parent.left == node[i]:
            	# 左分支设置为0
            	code_list[i] = "0" + code_list[i]
            else:
            	# 右分支设置为1
            	code_list[i] = "1" + code_list[i]
            # node指向父节点
            node = node.parent
	return code_list

注意：我们在为左右分支分别设置0和1时，需要注意设置的顺序不能变。即0或1必须在code_list[i]的前面。因为我们编码需要从叶子结点先到达根结点然后在回溯时输出编码的值，而代码从叶子结点到根结点的过程中就开始记录编码的值，所以必须把后得到的值放在现有值前面才能得到正确的编码顺序。

六：树的基本性质

1. 树的概念

​ 树是n(n>=0)个结点的有限集合，在任一棵非空树中：

​ 有且仅有一个称为根的结点

​ 其余结点可分为多个互不相交的集合，而且这些集合中的每一集合都本身又是一棵树，称为根的子树。

​ 森林是m(m>=0)个互不相交的树的集合

2. 树的性质

   • n个结点的树中有n-1条边。

     证明：除树的根结点外每个结点有且只有一个直接前驱，除树的根结点之外的结点数等于所有结点的分支数。

   • 在度为k的树中，第i层至多有k^i-1个结点。

     证明：最多的情况为，除了叶子结点，每个结点的度都是k

   • 度为k、高为h的树中至多有(k^k-1/k-1)个结点

     证明：最多的情况为，除了叶子结点，每个结点的度都是k

   • 具有n个结点的度为k的树最小高度为 : log_k(n*(k-1)+1)（如果取得小数则向上取整），最大高度为：n-k+1

     证明：当树为满k叉树时，高度是最小的，由第三个性质推导而来，n = (k^k-1/k-1) ==> k^h=n*(k-1)+1 ==> h = log_k(n*(k-1)+1)。最大高度的情况为，从根结点开始，每一层只有一个结点，只有最后一层有k个结点。

3. 树的存储

   ​ 树的存储结构有很多，既可以采用顺序存储结构，也可以采用链式存储结构。但无论采用哪种存储方式，都要求存储结构不仅能存储各结点本身的数据信息，还要能惟一地反映树中各结点之间的逻辑关系。

   ​ 常用的存储方式有：

   • 子节点引用表示
   • 父节点引用表示(双亲结点法)
   • 子节点表表示(孩子链表法)
   • 长子兄弟表示(二叉链表法)
   • list递归实现

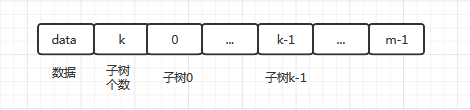
4. 子节点引用表示

   

   在最大m度结点表示的n个结点的树中，我们为每个结点分配m+2个空间，其中第一个指针域用来存储数据，第二个指针域用来存储子结点的个数，剩下的指针域用来存储子节点的地址信息。

   性质：在这样的一棵树中，会产生n*(m-1)+1个空指针域

   证明：共有n个结点，每个结点有m个指针域，即共有n*m个指针域，由于根结点没有指针域，所以共用了n-1个指针域。所以共产生n*m-(n-1)个空指针域，即产生n*(m-1)+1个空指针域。

   优点：能直接反映子树的机构，操作方便灵活，很好的支持树结构的变动。

   缺点：出现大量空闲的结点指针域

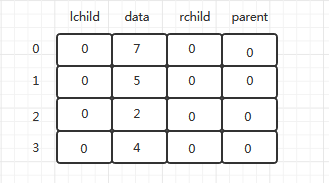
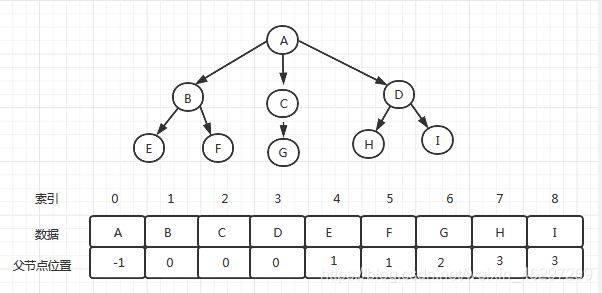
5. 父节点引用(双亲表示法)

   子节点引用会导致大量空闲的结点指针域，所以我们一般不会采用此种表示方法。父节点引用可以避免此类问题。

   用一种连续的存储空间存储树中的各结点，树中除根外的每个结点都有惟一的一个双亲结点，所以每个结点存储元素本身的信息和结点的双亲结点的位置。

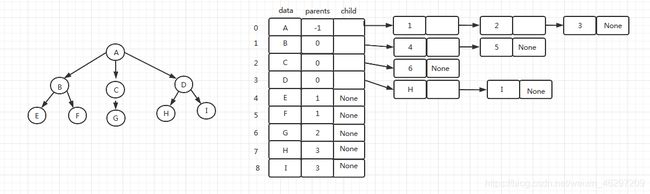
如上图中的树，先将树按从上到下，从左到右的顺序排序，然后记录对应元素的父结点索引，从而得到一个存储着父节点数据和索引的列表。

优点：存储开销小，找双亲很容易，适合于寻找双亲的场合

缺点：找孩子难

# 双亲类结点类(data.parent)
class CNode:
	def __init__(self,data,parent):
		self.data = data
		self.parent = parent
nodes = []

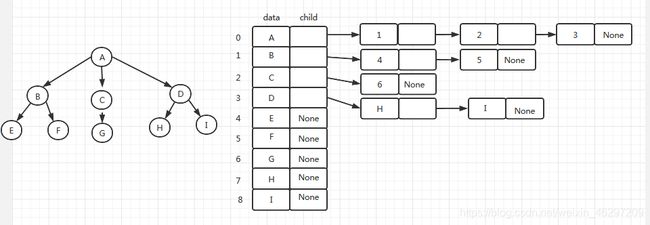
6. 子节点表表示(孩子链表法)

   ​ 孩子链表示法是通过保存每个结点的孩子结点的位置，表示树中结点之间的结构关系。每个结点的孩子结点用单链表存储，再用含n个元素的列表指向每个孩子链表。

   ​ 图解：

# 孩子结点类
class CNode:
	def __init__(self,child,next=None):
		self.child = child
		self.next = next
		
# 双亲结点类
class PNode:
	def __init__(self,data,firstchild=None):
	self.data = data
	self.firstchild = firstchild

# 存放双亲结点的列表
nodes = []

优点：找孩子容易，适合用于寻找孩子的场合

缺点：找双亲难

​ 如果既想要寻找子结点又想要寻找父结点，可以将父结点表示法与子结点法相结合的方法来构建。

图解：

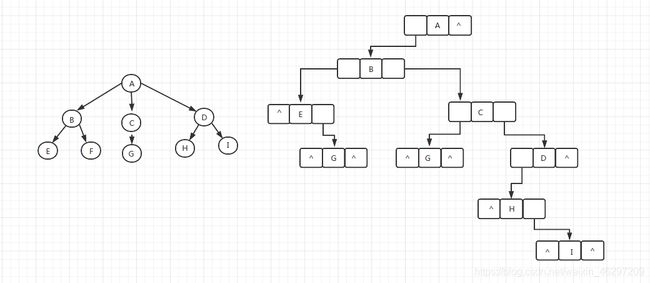
7. 长子兄弟表示法(二叉链表表示法)

   ​ 长子兄弟表示法用二叉链表作为树的存储结构。将树中的多支关系用二叉链表的双分支关系体现。

   ​ 结点的左指针指向它的第一个孩子(长子)结点

   ​ 右指针指向它的下一个兄弟结点

   ​ 图解如下：

   

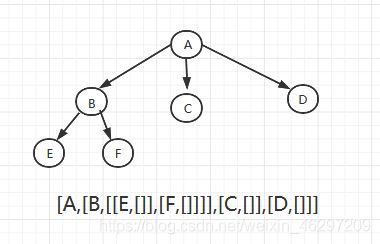
8. list递归实现(python特有)

   树(根结点，一组子树) ===》用二元组来表示树：列表或元组

   存放方式与二叉树相似

   图解：

七：树，森林与二叉树之间的相互转换

​ 转换如图所示：

​

​ 由图可见：上图中的树与二叉树在内存中的存储结构是完全相同的，只是画图时为了区分树的层次而看起来有所不同。所以我们针对树的操作，比如遍历，增删结点等，都可将树先转换为二叉树然后再进行操作。

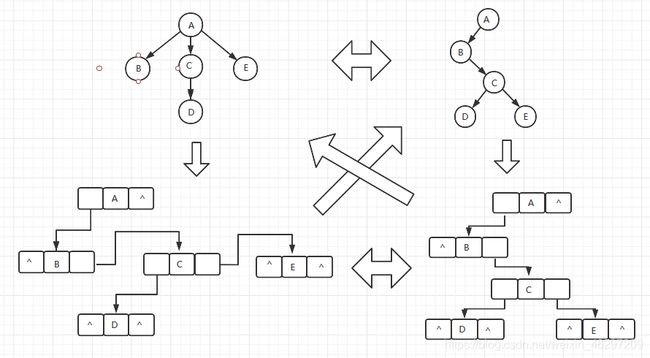
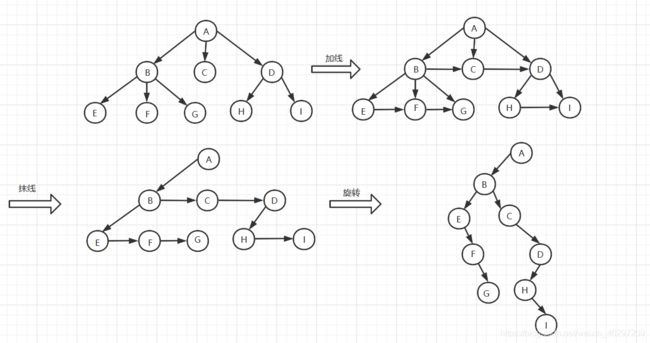
1. 树转换为二叉树

   方法：在树中的长子即是二叉树中的左孩子，在树中的兄弟即是二叉树中的右孩子。具体如下

• 加线：在兄弟之间加一连线

• 抹线：对每个结点，除了其左孩子外，去除其与其余孩子之间的关系

• 旋转：以树的根结点为轴心，将整树顺时针转45^。

  转换图解如下：

由图中可以看出：树转换成的二叉树其右子树一定为空

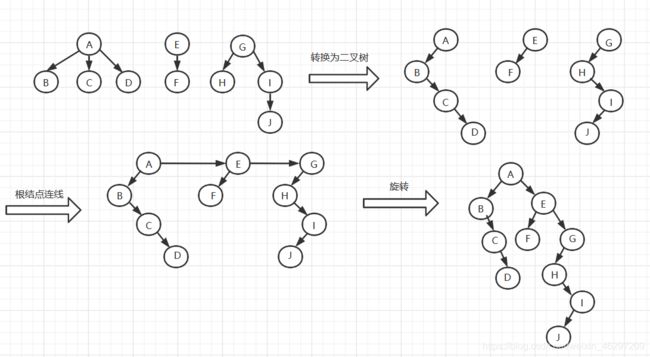
2. 森林转换为二叉树的方法：

• 将各棵树分别转换为二叉树

• 将每棵树的根节点用线相连

• 以第一棵树根结点为二叉树的根，再以根结点为轴心，顺时针旋转45^。

  转换图解如下：

3. 二叉树转换为树

• 加线：若p结点是双亲结点的左孩子，则将p结点的右孩子，右孩子的右孩子，…沿分支找到所有右孩子，都与p的双亲用线连起来

• 抹线：抹掉原二叉树中双亲与右孩子之间的连线

• 调整：将结点按层次排列，形成树结构

  转换图解如下：

4. 二叉树转换为森林

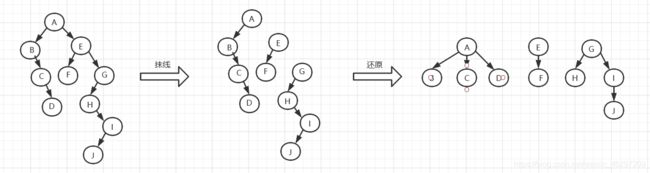
   这里我们需要先搞清楚一个问题，即如何判断一个二叉树对应的是树还是森林。如果一个二叉树的根结点有右子树那么它对应的就是森林，没有则对应树。

• 抹线：将二叉树中根结点与其右孩子连线，及沿右分支搜索到的所有右孩子间连线全部抹掉，使之变成孤立的二叉树。

• 还原：将孤立的二叉树还原成树

  转换图解如下：

八：树、森林的遍历

​ 树和森林的遍历总共有3中，比二叉树的遍历少了一个中序遍历，如下：

• 层次遍历：从上到下，从左到右依次遍历树中各个结点
• 先根遍历：先访问根，然后依次先序遍历每一棵子树
• 后根遍历：依次后序遍历根的每一棵子树，然后访问根

1. 树的遍历

​ 如下图所示 ：

​ 先根遍历序列：A B E F C G D H I

​ 后根遍历序列：E F B G C H I D A

​ 注：树的先根遍历与这棵树对应的二叉树的先序遍历是相同的，树的后根遍历对应二叉树中的中序遍历

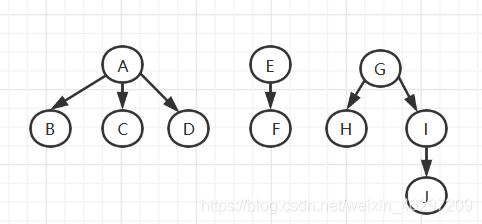
2. 森林的遍历

• 先根遍历

  对森林中的每一棵树进行先序遍历；

  先根遍历森林中第一棵树的子树森林；

  先根遍历森林中(除第一棵树之外)其余树构成的森林

  如下图所示：
  
  先根遍历序列为：A B C D E F G H I J

注：先根遍历森林和先序遍历与该森林对应的二叉树结果相同

• 后根遍历

对森林中的每一棵树进行后序遍历

若森林不空，则

后根遍历森林中的第一棵树的子树森林；

访问森林中第一棵树的根结点；

后根遍历森林中(除第一棵树之外)其余树构成的森林

上图后根遍历的序列为：B C D A F E H J I G

注：后根遍历森林和中序遍历与该森林对应的二叉树结果相同