递归程序设计方法

题目一：一个人赶着鸭子去每个村庄卖，每经过一个村子卖去所赶鸭子的一半又一只。这样他经过了七个村子后还剩两只鸭子，问他出发时共赶多少只鸭子？经过每个村子卖出多少只鸭子？

1.题目分析
根据题目可知这个问题如果要求得最开始时的鸭子数必须知道每经过一个村子卖了多少只鸭子以及买完鸭子后剩余鸭子的数目。根据最后剩余的鸭子数通过逆序进行推导运算得到前经过时一个村子的鸭子数，最后得到刚开始时的鸭子数。因此本题可以使用递归方法进行运算。
2.算法构造
要使用递归的方法就必须设计递归函数的递归体和递归出口，根据题目可以推导出有如下递归表达式：

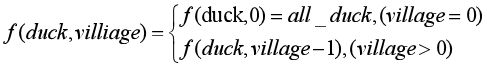
当经过的村子数大于0时，进行递归操作，得出经过前一个时村子的鸭子数，当村子数为0时停止递归，得到总的鸭子数。
3.算法实现
1、递归方法实现：使用python语言实现，设计了一个递归函数，一个主函数。主函数进行传参控制经过的村子数以及最后剩余的鸭子数。递归函数对总的鸭子数进行求解。
递归函数实现：

def sellduck(duck,village):
    """
    定义递归函数
    :param duck: 鸭子的数目
    :param village: 经过的村子数
    :return:对函数进行递归，返回鸭子的总数
    """
    if village>0:  # 函数的递归体

        duck = (duck+1)*2
        sell_duck = duck/2+1  # 经过每个村子卖掉的鸭子数
        print("经过第%s个村子共卖了%s只鸭子" % (village, sell_duck))
        return sellduck(duck, village-1)
    else:   # 递归的结束条件

        return  duck

主函数实现

def main():
    sellduck(2, 7)

2、非递归方法实现：非递归方法和递归方法的思路相同，区别是非递归是通过循环实现的，需要设计循环的开始和结束，其他的部分都是相同的。

def sellduck(duck, village):
    """
    非递归方法实现卖鸭子的问题，通过循环结构实现
    :param duck:鸭子的数目
    :param village:经过的村子数
    :return:返回刚开始时的鸭子数
    """
    for i in range(village):  # 循环条件
        duck = (duck + 1) * 2
        sell_duck = duck / 2 + 1  # 经过每个村子卖掉的鸭子数
        print("经过第%s个村子共卖了%s只鸭子" % (village, sell_duck))
    return duck


    def main():
    print("刚开始共有%s只鸭子" % sellduck(2, 7))

4、运行结果

题目二：角谷定理。输入一个自然数，若为偶数，则把它除以2，若为奇数，则把它乘以3加1。经过如此有限次运算后，总可以得到自然数值1。求经过多少次可得到自然数1。

1.题目分析
根据题目可以知道，该程序的主要实现的是对一个自然数的判断过程，然后再经过一些操作最后可以得到结果1。因此通过递归方法可以完成该程序。
2.算法构造
使用的递归的方法就需要设计递归体和递归出口，改题目主要是要得到结果1，因此该递归函数的出口就是当number为1时，递归体为对自然数的操作步骤，通过step步后可以得到1.因此该程序的递归表达式如下：

3.算法实现
1、该程序设计了一个递归函数，一个主函数。递归函数用来实现对自然数的循环操作，主函数调用递归函数。
递归函数：

def judge(number, step):
    """
    递归函数的实现
    :param number: 传入的自然数
    :param step: 将一个自然数转化为1所需要的步骤
    :return 操作所用的步骤数，递归调用函数
    """
    print(number)
    step += 1
    if number != 1 and number > 0:  # 函数的递归体
        if number % 2 == 0:
            number /= 2
        else:
            number = number*3 + 1
        return judge(number, step)
    elif number == 1:  # 递归的结束条件
        return step

主函数：

def main():
    print("总共需要%s步" % judge(22, 0))

2、非递归方法实现：非递归解决该问题使用到了while循环，当数不为1时，一直保持对其进行规定的操作，当为1是，输出返回结果。

def judge(number, step):
    """
    非递归方法实现买角谷定理的问题，通过循环结构实现
    :param number: 传入的自然数
    :param step: 将一个自然数转化为1所需要的步骤
    :return 操作所用的步骤数，循环调用函数
    """
    print(number,end='  ')
    step += 1
    while number != 1:  # 循环条件
        if number != 1 and number > 0:
            if number % 2 == 0:
                number /= 2
            elif number %2 != 0:
                number = number*3+1
            return judge(number, step)
    if number == 1:
         return step

def main():
    print("总共需要%s步" % judge(22, 0))

4、运行结果
在调试过程中遇到了maximum recursion depth exceeded in comparison这样的错误，在网上查到这个错误是由于递归次数超过python所限制的最大递归次数，大概有900多次，但很显然，我这个程序是达不到这么多递归次数的。

最后经过修改发现错误的原因是在于有一个语句出现错误，刚开始在判断是奇数后的操作里面我写的是 number*=3+1，最后修改成了number=number*3+1,但这样的错误我不知道为什么会导致递归次数超过限制,我个人感觉应该是没有影响的。

程序的结果

5.经验归纳
通过这次作业的完成，我对于递归的方法有了更深的了解，在使用递归解决问题时首先要对问题进行分析，判断使用递归简单还是循环更简单。在使用递归时要按照递归的规定设计好递归出口和递归条件。

以下是我在网上看到的一些比较好的递归方法总结：
来源于该博客 https://blog.csdn.net/welber/article/details/6447513
递归的解释：
（1）递归就是在过程或函数里调用自身；
（2）在使用递归策略时，必须有一个明确的递归结束条件，称为递归出口。

递归算法一般用于解决三类问题：
（1）数据的定义是按递归定义的。（比如Fibonacci函数）
（2）问题解法按递归算法实现。（回溯）
（3）数据的结构形式是按递归定义的。（比如树的遍历，图的搜索）

递归的缺点：递归算法解题的运行效率较低。在递归调用的过程当中系统为每一层的返回点、局部量等开辟了栈来存储。递归次数过多容易造成栈溢出等。

递归程序的基本步骤：
每一个递归程序都遵循相同的基本步骤：
1.初始化算法。递归程序通常需要一个开始时使用的种子值（seed value）。要完成此任务，可以向函数传递参数，或者提供一个入口函数，这个函数是非递归的，但可以为递归计算设置种子值。
2.检查要处理的当前值是否已经与基线条件相匹配（base case）。如果匹配，则进行处理并返回值。
3.使用更小的或更简单的子问题（或多个子问题）来重新定义答案。
4.对子问题运行算法。
5.将结果合并入答案的表达式。
6.返回结果。

基线条件（base case）。基线条件是递归程序的最底层位置，在此位置时没有必要再进行操作，可以直接返回一个结果。所有递归程序都必须至少拥有一个基线条件，而且必须确保它们最终会达到某个基线条件；否则，程序将永远运行下去，直到程序缺少内存或者栈空间。

要写一个递归的程序的实现步骤：
1.一个基线条件。请在递归函数的一开始就处理这个基线条件。
2.一系列的规则，使对递归函数的每次调用都趋进于直至达到这个基线条件。