【LeetCode】223. Rectangle Area

Rectangle Area

Find the total area covered by two rectilinear rectangles in a 2D plane.

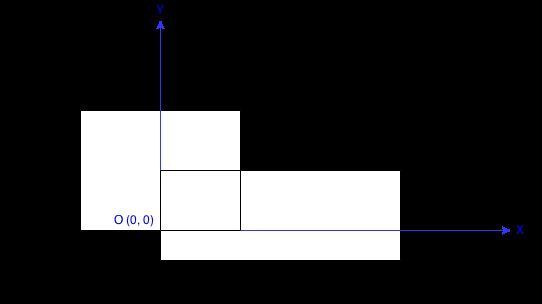
Each rectangle is defined by its bottom left corner and top right corner as shown in the figure.

Assume that the total area is never beyond the maximum possible value of int.

Credits:
Special thanks to @mithmatt for adding this problem, creating the above image and all test cases.

 

两个矩形分别面积之和减去重叠面积。

记(A,B)(C,D)表示第一个矩形rect1，(E,F)(G,H)表示rect2

一、有4种情况，rect1和rect2完全不重叠

1、rect1整个在rect2右边，即 A >= G

2、rect1整个在rect2左边，即 C <= E

3、rect1整个在rect2上边，即 B >= H

4、rect1整个在rect2下边，即 D <= F

二、计算重叠面积（即长、宽）

1、计算宽

(1)当 A <= E 时，

重叠部分的最左边即rect2的最左边(E)

重叠部分的最右边可能是rect1的最右边(C)，也有可能是rect2的最右边(G)

(2)当 A > E 时，

重叠部分的最左边即rect1的最左边(A)

重叠部分的最右边可能是rect1的最右边(C)，也有可能是rect2的最右边(G)

2、计算长

(1)当 D <= H 时，

重叠部分的最上边即rect1的最上边(D)

重叠部分的最下边可能是rect1的最下边(B), 也有可能是rect2的最下边(F)

(2)当 D > H 时，

重叠部分的最上边即rect2的最上边(H)

重叠部分的最下边可能是rect1的最下边(B), 也有可能是rect2的最下边(F)

 

class Solution {
public:
    int computeArea(int A, int B, int C, int D, int E, int F, int G, int H) {
        int width;
        int height;
        
        if(A >= G // rect1 is in the right of rect2
        || C <= E // rect1 is in the left of rect2
        || B >= H // rect1 is above rect2
        || D <= F // rect1 is below rect2
        )
        {// no overlap
            width = 0;
            height = 0;
        }
        else
        {// overlap
            if(A <= E)
                width = min(G - E, C - E);
            else
                width = min(C - A, G - A);
                
            if(D <= H)
                height = min(D - B, D - F);
            else
                height = min(H - F, H - B);
        }
        return (C-A)*(D-B)+(G-E)*(H-F)-height*width;
    }
};