图像生成：GAN网络(数学原理）

GAN网络经常会见到或用到，但感觉对其理解不够深入，写此博客记录一下，方便今后查阅。只看笔记估计很难看懂，推荐两个视频：
晟腾CANN训练营
GAN论文精读

1. 首先是GAN的基本原理

#pic_center =x250)
GAN的整个训练对抗过程可以由下式表示出来：

${\min }_G{\max }_{D}V(D,G)={\mathbb{E}}_{\mathbf{x}\sim p_{\text{data }}(\mathbf{x})}[\log D(\mathbf{x})]+{\mathbb{E}}_{\mathbf{z}\sim p_{\mathbf{z}}(\mathbf{z})}[\log (1-D(G(\mathbf{z})))]$

其中G（generator）是想让整个式子的值V尽可能小，而D（discriminator）想让V尽可能大。

• 对于右边第一项：
  ${\mathbb{E}}_{\mathbf{x}\sim p_{\text{data }}(\mathbf{x})}[\log D(\mathbf{x})]$
  x是data中的数据，D为了使该项更大，对真实数据x的判别为真的概率D(x)就要越大。
• 对于右边第二项：
  ${\mathbb{E}}_{\mathbf{z}\sim p_{\mathbf{z}}(\mathbf{z})}[\log (1-D(G(\mathbf{z})))]$
  z是随机噪声，D为了使该项更大，对假数据G(z)的判别为真的概率D(G(z))就要越小。
  G为了使该项越小，其生成的假数据G(z)就要越像真的，才能骗到D使得D(G(z))越大，从而使得第二项整个越小。

2. GAN的训练过程

2.1 训练流程

简单来说其训练过程如下：

• 训练判别器D，训练k步（需要调节的超参，即D可能需要更多训练）。采样噪声z和图片x，根据前述的公式求梯度来更新判别器D。
• 训练生成器G，只训练一步且只需采样噪声z，根据前述公式求梯度更新生成器G。

2.2 实际训练时使用更好优化的损失函数

观察G和D都有的损失项：
$J^{(G)}=\frac{1}{2}{\mathbb{E}}_{\mathbf{z}}\log (1-D(G(\mathbf{z})))$
图中Minimax（零和博弈）线是该损失项关于D(G(z))的曲线，在网络训练初期，G所生成的图像很好判断，D会给他很低的置信度，这时梯度是很小的，网络的学习很慢，只有当后期时D较难判断时，更新梯度才会较大。

但我们肯定希望是G生成较差时（训练初期）会有较大梯度进行更新才对。
所以实际使用中，我们选择非饱和启发式博弈（Non-saturating heuristic）：
$J^{(G)}=-\frac{1}{2}{\mathbb{E}}_{\mathbf{z}}\log D(G(\mathbf{z}))$
观察它的梯度，是更合适的：初期训练时梯度较大，后期较小。

4. GAN的问题

• 不好训练：G和D交替训练，其中一个不能训练太好，即对抗平衡不能被打破。
• 模式坍缩：只产生一种甚至一张迷惑性很高的图，但即可骗过辨别器D。

5. 从数学方面看生成器G的学习

$P_{\text{data }}(\mathrm{x})$ :真实图片分布，
$P_G(x,\theta ):G$ 生成的图片分布，$\theta$是生成器G的参数，
在真实分布中取一些数据 $\left\{x^1,x^2,\dots ,x^m\right\}$，
生成模型的最大似然估计：$L={\prod }_{i=1}^m{P}_G\left(x^i;\theta \right)$

$\begin{array}{rl}{\theta }^{\ast }& =\arg \underset{\theta }{\max }\prod _{i=1}{P}_G\left(x^i;\theta \right)\\ & =\arg \underset{\theta }{\max }\log \prod _{i=1}^m{P}_G\left(x^i;\theta \right)\\ & =\arg \underset{\theta }{\max }\sum _{i=1}^m\log P_G\left(x^i;\theta \right)\\ & \approx \arg \underset{\theta }{\max }{E}_{z\sim P_{\text{data }}}\left[\log P_G(x;\theta )\right]\\ & =\arg \underset{\theta }{\max }{\int }_z{P}_{\text{data }}(x)\log P_G(x;\theta )dx-{\int }_x{P}_{\text{data }}(x)\log P_{\text{data }}(x)dx\\ & =\arg \underset{\theta }{\max }{\int }_x{P}_{\text{data }}(x)\left(\log P_G(x;\theta )-\log P_{\text{data }}(x)\right)dx\\ & =\arg \underset{\theta }{\min }{\int }_x{P}_{\text{data }}(x)\log \frac{P_{\text{data }}(x)}{P_G(x;\theta )}dx\\ & =\arg \underset{\theta }{\min }KL\left(P_{\text{data }}(x)\Vert P_G(x;\theta )\right)\end{array}$

• 中间这个 $E_{z\sim P_{\text{data }}}\left[\log P_G(x;\theta )\right]$的展开没看懂。。。先记下来吧
  期望的定义： $E_{x\sim p}[f(x)]={\int }_x[P(x)f(x)]dx$

最后可推得：求 ${\theta }^{\ast }$就是求使得 $P_{\text{data }}(x)$ 与$P_G(x;\theta )$的KL散度最小（两者相等时）时$\theta$的取值。

• 题外话：KL散度
  考虑某个未知的分布 p(x)，假定用一个近似的分布q(x)对它进行建模。如果我们使用q(x)来建立一个编码体系，用来把×的值传给接收者，那么由于我们使用了q(x)而不是真实分布p(x)，平均编码长度比用真实分布px)进行编码增加的信息量(单位是nat )为:
  $\begin{array}{rl}KL(p\Vert q)& =-\int p(x)\ln q(x)dx-\left(-\int p(x)\ln p(x)dx\right)\\ & =-\int p(x)\ln \left[\frac{q(x)}{p(x)}\right]dx\end{array}$
  p，q相等时KL散度为0。注意，这不是一个对称量,即 $KL(p\Vert q)\ne KL(q\Vert p)$

6. 训练：

6.1 先固定G，训练D

基于GAN的对抗过程：
${\min }_G{\max }_{D}V(D,G)={\mathbb{E}}_{\mathbf{x}\sim p_{\text{data}}(\mathbf{x})}[\log D(\mathbf{x})]+{\mathbb{E}}_{\mathbf{x}\sim p_{\mathbf{x}}(\mathbf{z})}[\log (1-D(G(\mathbf{z})))]$

那么固定G，且由上图的定律，那么V就可以由下式的结果表达
$\begin{array}{rl}V& =E_{x\sim P_{\text{data }}}[\log D(x)]+E_{x\sim P_G}[\log (1-D(x))]\\ & ={\int }_x{P}_{\text{data }}(x)\log D(x)dx+{\int }_x{P}_G(x)\log (1-D(x))dx\\ & ={\int }_x\left[P_{\text{data }}(x)\log D(x)+P_G(x)\log (1-D(x))\right]dx\end{array}$
接下来解$D^{\ast }(x)$:

将解得的$D^{\ast }(x)$带入原式中，得到下式:

最后V推导成了Jensen-Shannon散度与一个常数的和。
其中Jensen-Shannon散度如下式定义，是一个对称量。

所以可以这么说：
在优化判别器D时，其实是在学习如何度量JS散度（度量得更准）。
在优化生成器G时，其实是在最小化JS散度。

6.2 GAN为啥不好训练

有些理论目前看不懂，先记下来吧

上面这个结论大概的意思就是JS散度容易为0，有点类似于坏死不起作用的情况。

前面有提到具体使用时一般使用非饱和启发式博弈替代零和博弈：

最小化KL散度和最大化JS散度是相反的两个任务。所以不好训练。

• 模式坍缩的原因：
  
  对KL散度分析，由于KL散度不对称 ：（此处也不是很理解）
  左图：因为KL散度的性质，G生成的分布需要兼顾data的两个峰，其KL散度才小
  右图：因为Peverse KL散度的性质，G生成的分布只要能跟住data的一个峰其KL散度就很小，前述的 ${\mathbb{E}}_{x\sim P_g}\left[-\log D^{\ast }(x)\right]$是包含的，所以容易发生模式坍缩。

回顾全程：
我们由对抗博弈的过程推导出其实GAN网络的优化过程和KL和JS散度有关，由于这最小化两个散度有各种问题，也就解释了GAN不好训练。

7. 后续几种常见的GAN

7.1 WGAN

JS散度问题很多，作者尝试换个指标去衡量：

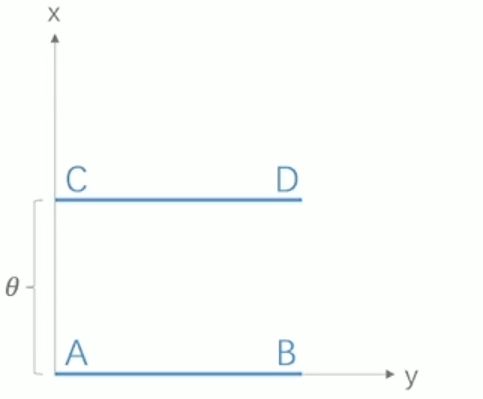
上图 CD和AB两个分布，其KL，JS散度以及Wasserstein距离如下：

$\begin{array}{rl}& KL⟨P_1\Vert P_2)=KL\left(P_1\Vert P_2\right)=\{\begin{array}{ll}+\infty & \text{ if }\theta \ne 0\\ 0& \text{ if }\theta =0\end{array}\\ & JS\left(P_1\Vert P_2\right)=\{\begin{array}{ll}\log 2& \text{ if }\theta \ne 0\\ 0& \text{ if }\theta -0\end{array}\\ & W\left(P_0,P_1\right)=|\dot{\varphi }|\text{ (क्ष) }\end{array}$
此时JS散度可以说是坏死的，但W距离仍能工作。

我们看如何使GAN去优化W距离：

所以对GAN做了如下修改：

• 判别器最后一层去掉sigmoid：
• 生成器和判别器的loss不取log
• 每次更新判别器的参数之后把它们的绝对值截断到不超过一个固定常数c
• 不要用基于动量的优化算法（包括momentum和Adam)，推荐RMSProp，SGD也行
  最后一点是试出来的，前三个是有理论依据的。

GAN不好训练的问题得到了很好的解决。

7.2 CGAN

给GAN个标签，让其只生成这一类别的标签。

7.3 CycleGAN

7.4 StyleGAN：可以精细控制生成的图像的属性

暂时没时间去了解，先放着吧