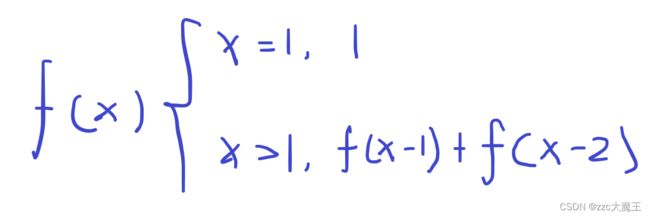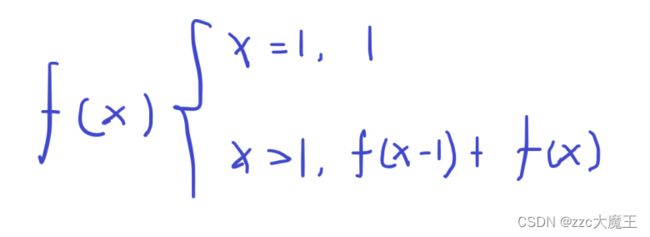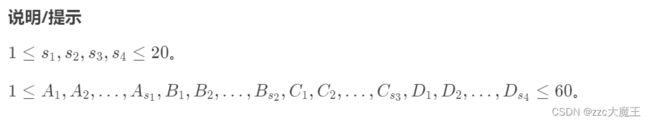★深度优先搜索+解空间树+递归，三合一详解

为什么这三个内容要放在一起讲？

如果单独分开讲那么 递归 和 深度优先搜索 这两个内容就会变得及其抽象，不适合新手入门

首先明确这三个内容的定义，由于深搜和递归过于抽象先说解空间树。

一、什么是解空间树？

解空间树是用树的结构来表达一个问题的解空间。（解空间就是这个问题的所有解。无论对错，包含所有情况）

以背包问题举例

你眼前有1，2，3三个物品，每个物品最多装 1 次，问你背包的不同情况有哪些。

随便想想的话，可以把1放进去，这是一种情况，1和2放进去，这又是一种情况，这样很容易考虑不全。

那么我们尝试以树的结构来描述出这个问题的所有解。

每个物品都只有 取 或者 不取 两种情况，所以易得下图

那么从根节点随便取一条路径开始走到底，就会成为这个解空间树的一个可能解，如果这个解是正确的，那么就是最优解。 

再换一个问题

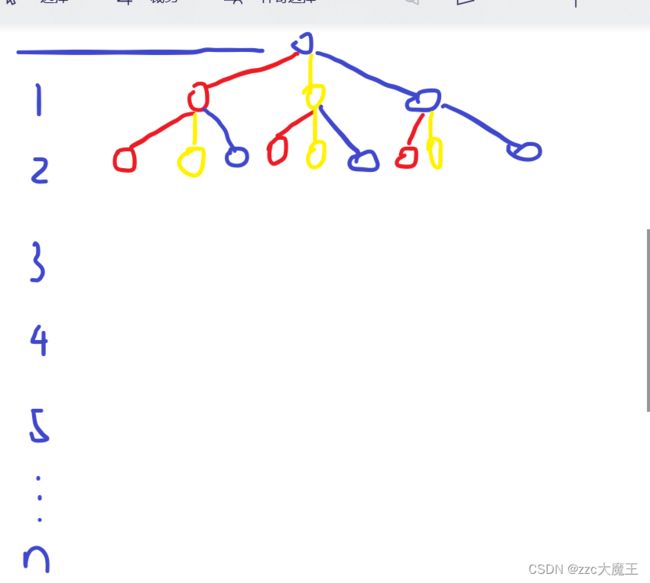
你眼前现在有一个方格纸，里面有很多个小方格，每个方格可以涂 红 黄 蓝 三种颜色，涂满这个方格纸，有多少种不同的方案。

画出解空间树，假设一共有n个方格，由每个格子有三种情况得出下图

太多了就不画完了，当1号格子涂蓝，2号可以是任意一个；当1号格子涂黄，2号可以是任意一个，从根节点走到底的任意一条路径，那么就是一个解。 

基本上就是这么个意思，用树来表达出解空间就可以。

二、什么是深度优先搜索（Deep-First-Search）？

取英文开头缩写即，DFS或者dfs，被众多神犇们戏称为大法师（dfs）或者 暴力算法

深度优先搜索是由两块部分组成的，即 深度优先 - 搜索。

深度优先就是以深度为优先。搜索就是在所给的数据中，搜索出解。

体现在解空间树中就是，每一步都要往下走一层，深度优先√

搜索就是走到底，找出一个解√

显而易见，深度优先不能100%保证能找出最优解，很可能会找出一大堆错的之后才找到对的那个，路径这么多那是必然的。

三、什么是递归?

递归就是调用自己。

 

 这样是调用别的函数，如果变成下面这样，调用自己就称为递归

---

明确了三个部分的定义之后就可以开始研究高深莫测的内容了

一、高深莫测的递归

 这个分段函数的意思就是，x=1的时候，f(1)=1，x>1的时候，f(x)=f(x-1).....多嘴了

把这个函数写成代码就是

int f(int x){
    if(x==1)return 1;
    else return f(x-1);
}

这就是递归喽。

因为有电脑，所以我们并不需要一步一步去算f(x)=f(x-1)=f(x-2).......=f(1)=1，虽然显而易见答案都是1，如果你能确保你的函数每一个都能推出正确解，那么电脑就会帮你自动算出来。

引用wiki的一句话：明白一个函数的作用并相信它能完成这个任务，千万不要跳进这个函数里面企图探究更多细节， 否则就会陷入无穷的细节无法自拔，人脑能压几个栈啊。递归 & 分治 - OI Wiki

这句话并不抽象（如果用解空间树的话），比如上面那个方格涂色，你知道每个方格都能涂三种颜色，那就开始思考！第一个涂红的时候 第二个涂红 黄 蓝，第一个涂黄的时候，第二个涂红 黄 蓝 @&*@#&*，你记得住吗？反正我记不住

再比如这个分段函数

 写成代码就是

int f(int x){
    if(x==1)return 1;
    else return f(x-1)+f(x-2);
}

当然如果有如下分段函数

代码肯定写的出来，但是算是肯定算不出来的，每个f(x)里面都还有一个f(x)，那我还算个锤子。

当x>1，f(x)=f(x-1)+f(x)，移动一下f(x)

得f(x-1)=0。

我要的是f(x)的取值，要f(x-1)干什么，f(x)都抵消掉了那就算不出来喽~

二、如何用递归正确的表达出解空间树

如果能用递归实现，那么就必然是DFS，因为代码是从上往下执行的，比如方格涂色

int f(int i,string color){

    f(i+1,"红");
    f(i+1,"黄");
    f(i+1,"蓝");
}

因为开头是红，所以调用自己会一直先执行开头这串代码，直到不满足某些条件，比如

int f(int i,string color){
    if(i>n)return 1;

    f(i+1,"红");
    f(i+1,"黄");
    f(i+1,"蓝");
}

当n个方块都被涂上红色之后，就会返回1，即一种情况，返回了之后我前面还有f(i+1,"黄")和红都还没有执行呢，那么返回去就近原则继续执行。

 到底了就返回最近的去执行，全部执行完了再上去执行历史内容。

不要深究！

我们可以理解为，每调用一次自己，就是产生一种状态，涂色一共有三种状态，那么就写三次递归。

int f(int i,string color){
    f(1,"红");
    f(1,"黄");
    f(1,"蓝");
}

这是给方块1涂色，但是我们要所有都涂色，所以直接i+1让代码自己去跑解空间树，i从0开始就可以举出所有情况。

当然上面那个会陷入死循环，因为反复给自己涂色。

所以要写成

int f(int i,string color){
    if(1无色)f(1,"红");
    1清空
    if(1无色)f(1,"黄");
    1清空
    if(1无色)f(1,"蓝");
}

避免先前情况造成影响，即

返回的时候，要先把原来的颜色去掉，不然就会反复上色。 

---

多说无益，这就是全部内容，接下来是例题时间。做题时多把dfs和解空间树结合，体会多了就懂了。可以选择跳过例题直接看总结

目录

总结

---

 

例题(递归+深搜)kkksc03考前临时抱佛脚 - 洛谷

 每个数组的范围都不超过20，好小啊，题目都在叫我们用暴力

两个大脑可以分别计算两道题目，也就是说尽可能让两个大脑的容量相近。

考虑解空间树，每道题都有两个状态，放在左脑或者右脑。

就两种状态，所以只需要递归两次

AC代码

#include 
using namespace std;
const int S=21;

int s1,s2,s3,s4,a[S],b[S],c[S],d[S],ans,minn;
inline void READ(){
    cin>>s1>>s2>>s3>>s4;
    for(int i=1;i<=s1;++i)cin>>a[i];
    for(int i=1;i<=s2;++i)cin>>b[i];
    for(int i=1;i<=s3;++i)cin>>c[i];
    for(int i=1;i<=s4;++i)cin>>d[i];
}
void dfs(int x[],int EDGE,int i,int ltot,int rtot){
    if(i==EDGE+1){//全都穷举完了，开始收集可行解，并且累计最优解
        minn=min(minn,max(ltot,rtot));
        return;
    }
    dfs(x,EDGE,i+1,ltot+x[i],rtot);//放在左脑
    dfs(x,EDGE,i+1,ltot,rtot+x[i]);//或者放在右脑
                                   //并接着穷举下一个
}
inline void WORK(){
    //给了四个数组，要分开判断
    minn=INT_MAX, dfs(a,s1,1,0,0),ans+=minn;
    minn=INT_MAX, dfs(b,s2,1,0,0),ans+=minn;
    minn=INT_MAX, dfs(c,s3,1,0,0),ans+=minn;
    minn=INT_MAX, dfs(d,s4,1,0,0),ans+=minn;
}
int main(){
    READ();
    WORK();
    cout<

---

例题（递归(+标记)+深搜）填涂颜色 - 洛谷

 依旧是n很小的一天啊，感叹

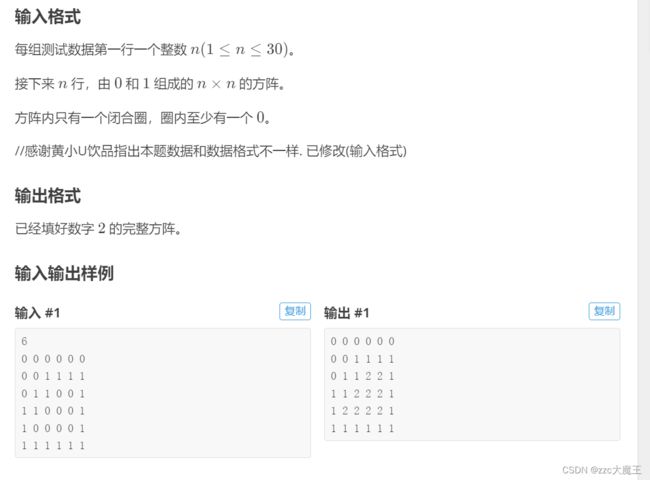
那么题目是让我们把1包围起来的0全部变成2，那么问题就可以变成所有的0是否可以变成2这个问题。

如果可以变成2那就变成2，不行那就不变，所以理论上是画不出解空间树的（直接就计算出答案）。

这道题一个递归就行了，从某个点出发，遍历周围的所有点（只走一遍，所以加个标记）

如果遇到1就return，如果出界了，那就说明不是我们需要染色的范围。

不过对于judge函数照样是可以写出解空间树的，判断所有情况即可。

 

AC代码

#include 
using namespace std;
const int N=35;

int n,a[N][N];
bool vis[N][N],can;

void judge(int x,int y){
    if(x<1||x>n||y<1||y>n){
        can=false;
        return;
    }
    if(a[x][y]==1)return;
    vis[x][y]=true;
    if(!vis[x-1][y])judge(x-1,y);
    if(!vis[x+1][y])judge(x+1,y);
    if(!vis[x][y+1])judge(x,y+1);
    if(!vis[x][y-1])judge(x,y-1);
}

int main(){
    cin>>n;
    for(int i=1;i<=n;++i)
        for(int j=1;j<=n;++j)
            cin>>a[i][j];

    for(int i=1;i<=n;++i)
        for(int j=1;j<=n;++j){
            if(a[i][j]==0){
                can=true;
                memset(vis,false,sizeof(vis));
                judge(i,j);
                if(can)a[i][j]=2;
            }
        }

    for(int i=1;i<=n;++i){
        for(int j=1;j<=n;++j){
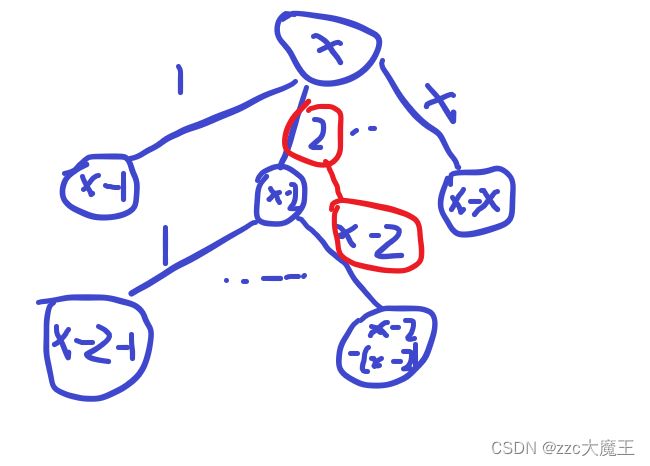
            cout<

---

例题（递归(+回溯)+深搜）自然数的拆分问题 - 洛谷

 对于一个数x，都可以从1拆到x，多拆就会变成负数，不需要。

 如果最后能变成0，那么输出一路上减去的数，就是答案。

 拆数，不能拆了退出，emmm，拆完了我输出什么东西

void dfs(int x){
    if(x==0){
        return;
    }
    for(int i=1;i<=x;++i){
        dfs(x-i);
    }
}

因为没东西记录一路上拆掉的数，所以加一个数组

int cnt[8],idx;
void dfs(int x){
    if(x==0){
        for(int i=0;i<=idx-1;++i){
            cout<

为什么要回溯？

不回溯的话先前的状态会保留，我们不需要多余的状态。

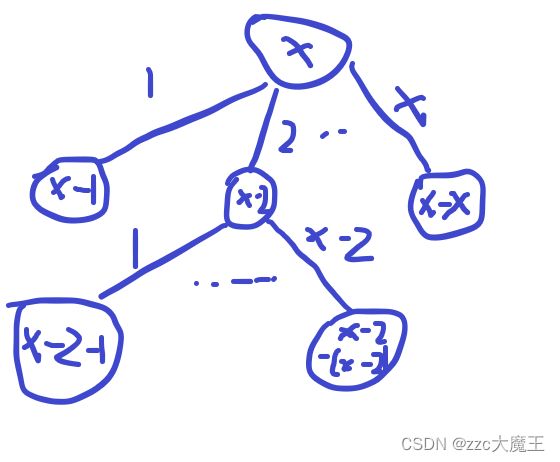
当我们去判断下一种情况的时候，红圈圈   圈起来的部分我们不再需要了，所以当递归结束的时候就要idx--

所以这里就会出现两种写法（即是否执行还原操作）

1.回溯时还原

如果用全局去记录，那么每一次新的状态我们就要回溯时执行还原操作

2.拒绝回溯时还原

如果把每一次的情况都放在函数的参数里面，那么下次新的情况，直接加在旧的情况上再进行递归即可。

但是这样会让递归时消耗的内存快速变大

好处是代码就会变得特别短

 

旧记录的基础上加上一个1，变成新记录（非常的方便不是吗）

但是肉眼可见，每一次都多了一个int数组，一般来说，这是不可取的。

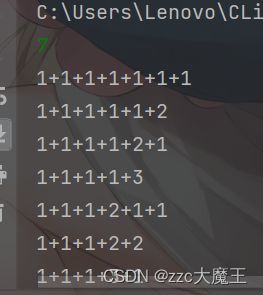
好！所以这道题AC了吗？

啊？，好像所有情况都拆出来了。

那就是拆重复了喽，拆了2之后就不能再往小的拆，否则会重复，所以保证最小拆的数是记录里面的最大值即可

int cnt[8],idx,minn;
void dfs(int x){
    if(x==0){
        for(int i=0;i<=idx-1;++i){
            cout<

等等，怎么最后还有个7。

特判一下，如果记录的idx内容只有1个，那就必然是自己（相当于没拆），那就不输出

AC代码（回溯版）

#include 
using namespace std;

int n;

int cnt[8],idx,minn;
void dfs(int x){
    if(x==0){
        if(idx==1)return;//特判
        for(int i=0;i<=idx-1;++i){
            cout<>n;
    dfs(n);
    return 0;
}

AC代码（无回溯版）

#include 
using namespace std;

int n;
void dfs(int x,int cnt[8],int idx,int max_elem){
    if(x==0&&idx>1)//事实上还要写个return来退出,但是数不会再被拆了
        for(int i=0;imax_elem?i:max_elem);
    }
}
int main(){
    cin>>n;
    dfs(n,new int[8],0,1);
    return 0;
}

真的很短欸，没骗你吧

但是输入的n是小于等于8的，内存都能差100字节还要多，n一大那内存就是爆炸级的增长。 

---

总结

解空间树是递归的具体体现，我们没必要用大脑去压一大堆栈来解决问题。

解决类似的问题都应该是：具现解空间树 -> 代码实现

而不是：头脑风暴 -> 有时对有时错的蒟蒻代码

 

 

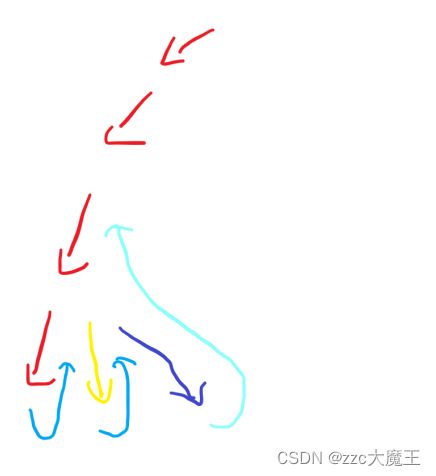
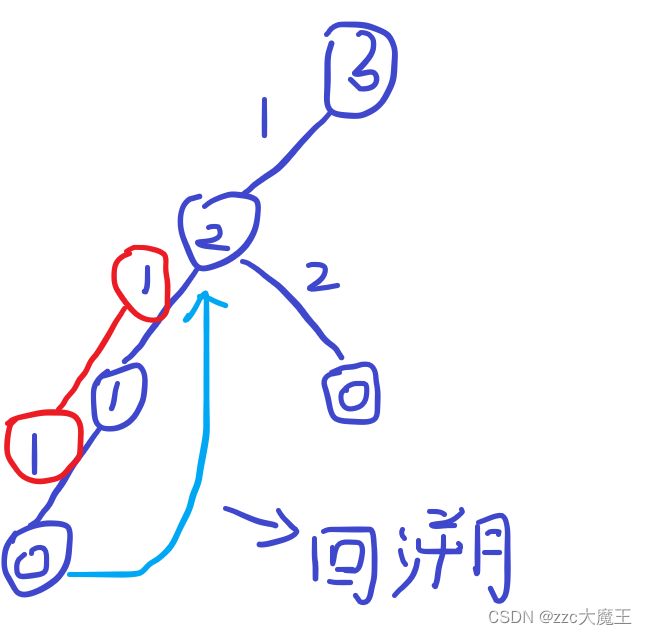
浅蓝色箭头要执行的操作，都写在递归下面的回溯部分里面。

每一部分都可以相互对应起来，f()下传的参数对应的是树中节点内存储的数据，递归一次就是产生一个儿子节点等等...