【论文阅读_序列推荐】Intent Contrastive Learning for Sequential Recommendation
【论文阅读_序列推荐】Intent Contrastive Learning for Sequential Recommendation
文章目录
- 【论文阅读_序列推荐】Intent Contrastive Learning for Sequential Recommendation
-
- 1. 来源
- 2. 介绍
- 3. 准备工作
-
- 3.1 问题定义
- 3.2 用于下一个项目预测的深度 SR 模型
- 3.3 SR中的对比SSL (self-supervised learning)
- 3.3.4 SR中的潜在因素建模
- 4. 模型方法
-
- 4.1 意图对比学习
-
- 4.1.1 建模SR的潜在意图
- 4.1.2 意图表示学习
- 4.1.3 与FNM进行意图对比的SSL
- 4.2 多任务学习
- 4.3 讨论
-
- 4.3.1 与SR中的对比性SSL的联系
- 4.3.2 时间复杂性和收敛性分析
- 5. 实验
-
- 5.1 数据集
- 5.2 结果
- 6. 总结
1. 来源
- 2022—WWW
- 论文地址:Intent Contrastive Learning for Sequential Recommendation
- code:ICLRec
2. 介绍
用户与物品的互动是由各种意图驱动的(例如,准备节日礼物,购买钓鱼设备等)。
- 然而,用户的潜在意图往往是无法被观察到的/潜在的,这使得利用这些潜在的意图来进行序列推荐(SR)具有挑战性。
因此,为了研究潜在意图的好处并有效地利用它们进行推荐,作者提出了意图对比学习(ICL),这是一种将潜在意图变量利用到SR中的一般学习范式。
- 其核心思想是从未标记的用户行为序列中学习用户的意图分布函数,并通过考虑学习到的意图,利用对比自监督学习(SSL)优化SR模型,以改进推荐。
- 具体地说,作者引入了一个潜在变量来表示用户的意图,并通过聚类来学习潜在变量的分布函数。
- 作者提出:通过对比SSL将学习到的意图利用到SR模型中,从而最大限度地提高序列视图与其相应意图之间的一致性。
- 在广义期望最大化(EM)框架内,参数训练在意图表示学习和SR模型优化步骤之间交替进行。
- 将用户意图信息融合到SR中也提高了模型的鲁棒性;并在四个真实数据集上进行的实验表明了所提出的学习范式的优越性,提高了性能,以及对数据稀疏性和噪声交互问题的鲁棒性。
3. 准备工作
3.1 问题定义
假设一个推荐系统有一组用户和物品,分别用 U 和 V表示。每个用户 ∈U 都有一个按时间顺序排序的交互项目序列, S u = [ s 1 u , s t u , . . . , s ∣ S u ∣ u ] S^u = [s^u_1, s^u_t, ..., s^u_{|S^u|}] Su=[s1u,stu,...,s∣Su∣u],其中 ∣ S u ∣ |S^u| ∣Su∣ 是用户 u u u 交互项目的数量, s t u s^u_t stu是 用户 u u u 在步骤 中交互的项目。
- 将 S u \mathbf{S}^u Su 表示为 S u S^u Su 的嵌入表示,其中 s t u \mathbf{s}^u_t stu 是项目 s t u s^u_t stu 的d维嵌入。
- 在实践中,序列被截断为最大长度 。
- 如果序列长度大于 ,则考虑最近的 动作。
- 如果序列长度小于 ,“填充”项目将被添加到左边,直到长度为 [12,13,36]。
- 对于每个用户 ,在给定序列 S u S^u Su 以及项目集 V的情况下,下一个项目预测任务的目标是预测 在 ∣ S u ∣ |S^u| ∣Su∣ + 1步骤中最有可能交互的下一个项目。
3.2 用于下一个项目预测的深度 SR 模型
现代序列推荐模型通常用深度神经网络对用户行为序列进行编码,以从(截断的)用户历史行为序列中建模序列模式。在不失去一般性的情况下,我们定义了一个序列编码器 f θ ( ⋅ ) f_{\theta}(\cdot) fθ(⋅),它对一个序列嵌入 S u \mathbf{S}^u Su 进行编码,并在所有位置步骤 H u \mathbf{H}^u Hu 上输出用户兴趣表示。特别是, h t u \mathbf{h}^u_t htu表示用户在位置 的兴趣。目标可以表述为寻找最优编码器参数 ,使所有位置步骤上给定序列的期望下一项的对数似然函数最大化:

这相当于最小化自适应的二元交叉熵损失,如下:

其中, s t u \mathbf{s}^u_t stu和 s n e g u \mathbf{s}^u_{neg} snegu表示目标项目 s t u s^u_t stu 和所有未被用户 u u u 交互的项目的嵌入。在等式中的求和运算符3的计算成本很高,由于|| 很大,因此,可以选择使用一个抽样的 softmax 技术来随机抽样每个序列中的每个时间步长的负项。 是s型函数。而 是指小批量大小作为SR模型。
3.3 SR中的对比SSL (self-supervised learning)
对比SSL的最新进展启发了推荐社区利用对比SSL,按照互信息最大化(MIM)原则,来融合一个序列的不同视图之间的相关性。SR中现有的方法可以看作是优化 MIM 下界的实例识别任务,如InfoNCE。其目的是优化正对和负对的间隙比例。在这种实例识别任务中,需要序列增强,如“掩码”、“作物”或“重新排序”,以创建SR中未标记数据的不同视图。
- 形式上,给定一个序列 s u s^u su 和一个预定义的数据转换函数集 G \mathcal{G} G,我们可以创建 s u s^u su 的两个正视图如下:
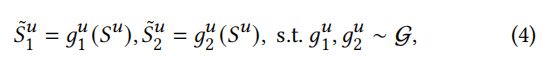
其中, g 1 u \mathcal{g}^u_1 g1u 和 g 2 u \mathcal{g}^u_2 g2u 是从 G \mathcal{G} G 中采样的转换函数,以创建序列 s u s^u su 的不同视图。通常,从相同序列创建的视图被视为正对,而任何不同序列的视图都被视为负对。 - 增广视图首先被序列编码器 f θ ( ⋅ ) f_{\theta}(\cdot) fθ(⋅) 编码到 H ~ 1 u \mathbf{\tilde{H}}^u_1 H~1u 和 H ~ 2 u \mathbf{\tilde{H}}^u_2 H~2u,然后输入一个“聚合”层,得到序列的向量表示,记为 h ~ 1 u \mathbf{\tilde{h}}^u_1 h~1u 和 h ~ 2 u \mathbf{\tilde{h}}^u_2 h~2u。
- 在本文中,为了简单起见,作者通过时间步长来“拼接”用户的兴趣表示。请注意,序列被预先拥有为具有相同的长度,因此它们在连接后的向量表示也有相同的长度。之后,我们可以通过InfoNCE损失来优化 :

其中,(·)为点积, h ~ n e g \mathbf{\tilde{h}}_{neg} h~neg 为负视图对序列 s u s^u su 的表示。
3.3.4 SR中的潜在因素建模
下一个项目预测任务的主要目标是优化等式 (1)。假设有 K 种不同的用户意图(例如,购买节日礼物,准备钓鱼活动等)。在形成意图变量 c = { c i } i = 1 K c=\{c_i\}^K_{i=1} c={ci}i=1K的推荐系统中,用户与某一项目交互的概率可以重写为:
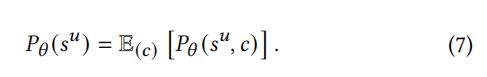
然而,用户的意图根据定义是潜在的。由于缺少变量的观察,我们处于“鸡和蛋”的情况,没有 c c c,我们不能估计参数 ,而没有 ,我们也不能推断 的值可能是什么。
稍后,我们将展示一个广义期望最大化框架为解决上述问题提供了一个方向。优化等式(7) 的基本思想通过EM是从对模型参数 的初始猜测开始,并估计缺失变量的期望值,即 E 步。一旦我们有了值 ,我们就可以最大化了等式(7) w.r.t 参数 ,即 M 步。我们可以重复这个迭代过程,直到可能性不能再增加为止。
4. 模型方法
图2 (b) 显示了在EM框架内提出的ICL的概述它交替执行 e步 和 m步,以估计意图变量上的分布函数(),并对模型参数进行优化。
- 在e步中,它通过聚类来估计()。
- 在m步中,它通过小批梯度下降考虑估计的()来优化 。
在每次迭代中,()和都会被更新。在接下来的章节中,我们首先推导出目标函数,以便将潜在的意图变量建模为一个SR模型,以及如何交替地优化目标函数,,并在第4.1节中的广义EM框架下估计的分布。然后,我们在第4.2节中描述了总体的培训策略。我们在第4.3节中提供了详细的分析,然后在第5节中提供了实验研究。

4.1 意图对比学习
4.1.1 建模SR的潜在意图
假设有个潜在的意图 c = { c i } i = 1 K c=\{c_i\}^K_{i=1} c={ci}i=1K,它会影响用户与项目交互的决定,然后基于等式(1)和(7),我们可以将目标改写如下:

然而,这个目标很难优化(因为我们很难去求积分)。相反,我们构造了一个等式的下界函数(8)并最大化了这个下限。形式上,假设意图 遵循分布(),其中 ∑ c Q ( c i ) = 1 \sum_c{Q(c_i)}=1 ∑cQ(ci)=1 和 Q ( c i ) ≥ 0 Q(c_i) \geq 0 Q(ci)≥0。然后,

基于詹森不等式,对于等式(9),有,

其中,∝代表“成比例”(即达到一个乘法常数)。当()=(|)时,不等式将相等。为简单起见,在优化下界时,我们只关注最后一个位置步骤,其定义为:
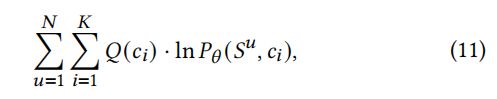
其中,()=(|)
到目前为止,我们已经发现了等式(8)的一个下界。
- 然而,我们不能直接优化等式(11),因为()是未知的。
- 相反,我们可以交替地优化了意图表示学习(E-step)和意图对比SSL与FNM(M-step)之间的模型,它遵循了一个广义的EM框架。我们将整个过程命名为意图对比学习(ICL)。
- 在每次迭代中,都将更新()和模型参数。
4.1.2 意图表示学习
为了学习意图分布函数(),我们用编码器 对所有序列 { S u } u = 1 ∣ U ∣ \{S^u\}_{u=1}^{|U|} {Su}u=1∣U∣ 进行编码,然后是一个“聚合层”,然后对所有序列表示 { h u } u = 1 ∣ U ∣ \{h^u\}_{u=1}^{|U|} {hu}u=1∣U∣进行-means聚类获取 集群。然后,我们可以定义分布函数()如下:
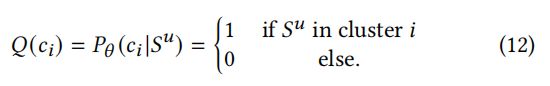
我们将 c i \mathbf{c}_i ci 表示为意图 c i c_i ci 的向量表示,它是 第 簇的质心表示。在本文中,为了简单起见,我们使用“聚合层”来表示所有位置步骤上的平均池化操作。
4.1.3 与FNM进行意图对比的SSL
我们已经估计了分布函数()。要最大化的等式(11),我们还需要定义 P θ ( S u , c i ) P_{\theta}(S^u, c_i) Pθ(Su,ci)。假设先验意图服从均匀分布,且给定 的 的条件分布是具有2归一化的各向同性高斯分布,则可以将 P θ ( S u , c i ) P_{\theta}(S^u, c_i) Pθ(Su,ci) 重写如下:

其中, h u \mathbf{h}^u hu和 c i \mathbf{c}^i ci 分别为 S u S^u Su \ c i c_i ci的向量表示。基于等式的(11)、(12)、(13),使等式最大化(11)相当于最小化以下损失函数:
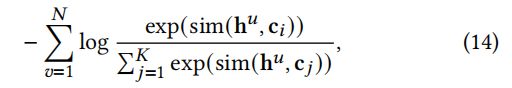
其中sim(·)是一个点积。我们可以看到,等式(14)与等式(6)的形式相似,其中,
- 等式(6)试图最大化两个个体序列之间的互信息;
- 而“等式”(14)最大化一个个体序列与其相应的意图之间的相互信息。
请注意,
- 在SeqCL中需要进行序列增强来为等式创建正视图 (6)。
- 而在ICL中,序列增强是可选的,因为给定序列的视图是它从原始数据集学习到的相应意图。
在本文中,我们应用序列增强来扩大训练集的目的,并基于等式(14)优化模型 。形式上,给定一批训练序列 { S u } u = 1 N \{S^u\}_{u=1}^N {Su}u=1N,我们首先通过等式(4)创建一个序列的两个正视图,然后优化以下损失函数:

其中 c n e g \mathbf{c}_{neg} cneg是给定批数据中的所有意图表示。然而,直接优化等式(16)会引入假阴性样本,因为一批处理中的用户可以有相同的意图。为了减轻假阴性样本的影响,作者提出了一个简单的策略来减轻影响:

其中,F是一组与小批处理中的 具有相同意图的用户。我们称之为假阴性缓解(FNM)。
4.2 多任务学习
作者用多任务训练策略训练 SR 模型,通过等式(17)联合优化ICL,通过等式(2)进行的主要的下一个项目预测任务,一个通过等式(5)进行的序列级SSL任务。在形式上,我们共同训练SR模型 f θ f_{\theta} fθ 如下:
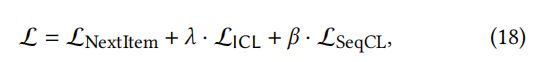
其中, 和 分别控制了 ICL 任务和序列级 SSL 任务的强度。特别地,作者在Transformer编码器上建立了学习范式,形成了模型ICLRec。
ICL是一个与模型无关的目标,因此也可以将其应用于 S3 -Rec 模型,该模型使用几个 L_SeqCL目标进行预训练,以捕获项目、相关属性和子序列之间的相关性,并使用L_NextItem目标进行微调。
4.3 讨论
4.3.1 与SR中的对比性SSL的联系
最近的方法在SR中的遵循标准的对比SSL,以最大限度地提高序列的两个正视图之间的互信息。例如,CL4SRec使用变压器编码序列,并最大化从原始序列中增强(裁剪、屏蔽或重新排序)的两个序列之间的互信息。然而,如果一个序列的项关系容易受到随机扰动,那么这个序列的两个视图可能不能揭示原始的序列相关性。ICLRec最大化了序列与其相应的意图原型之间的互信息。由于意图原型可以被认为是一个给定序列的积极观点,通过考虑所有序列的语义结构来学习,这反映了真正的序列相关性,ICLRec可以始终优于CL4SRec。
4.3.2 时间复杂性和收敛性分析
在训练阶段的每一次迭代中,我们提出的方法的计算代价主要来自于(·)的 e步估计和基于多任务训练的 的 m步优化。
- 对于e步,聚类的时间复杂度为(||),其中为嵌入的维数,为聚类中的最大迭代次数(本文为=20)。
- 对于m步,由于我们有三个目标来优化网络(·),因此时间复杂度为(3·(||^2 +||^2)。
因此,总体复杂性由术语(3·(||^2 ))主导,这是基于转换的SR的3倍,只有下一个项目预测目标,如SASRec。幸运的是,该模型可以有效地并行化,因为是变压器,我们把它留给未来的工作。在测试阶段,不再需要所提议的ICL和SeqCL目标,这使得模型具有相同的时间复杂度如SASRec((||))。
5. 实验
5.1 数据集
5.2 结果
6. 总结
在这项工作中,作者提出了一种新的学习范式ICL,它可以从用户交互中建模潜在的意图因素,并通过一个新的对比SSL目标将它们融合成一个顺序推荐模型。ICL是在一个EM框架内制定的,这保证了收敛性。详细的分析表明了ICL的优越性,并在四个数据集上进行的实验进一步证明了该方法的有效性。


