41、【匹配算法】KMP字符串匹配算法(C/C++版)
一、介绍
KMP算法是一种改进的字符串匹配算法,由D.E.Knuth,J.H.Morris和V.R.Pratt提出的,因此人们称它为克努特—莫里斯—普拉特操作(简称KMP算法)。
二、所解决的问题
解决字符串的匹配问题,即所谓模式匹配,可理解为在目标(字符串)中寻找一个给定的模式(也是字符串),返回目标和模式匹配的第一个子串的首字符位置。通常目标串比较大,而模式串则比较短小。
最简单的实现方法是暴力法,进行依次对比遍历,时间复杂度为O(n^2)。根据字符串自身中具有相同这一性质,可对其进行优化,设计了KMP字符串匹配算法,达到时间复杂度为O(m + n),其中m为模式串,n为目标字符串。
例如:
在所给定的文本串中,找出是否有其子文本串与模式串所匹配。
目标串:aabaabaaf
模式串:aabaaf
三、前置知识点
模式串:aabaaf
(1)前缀
包含首字符而不含尾字符,按原顺序组合的子串。
例:a、aa、aab、aaba、aabaa
(2)后缀
包含尾字符而不含首字符,按原顺序组合的子串。
例:abaaf、baaf、aaf、af、f
(3)最长相等(公共)前后缀
一个字符串中,具有相同前缀和后缀的字符串组合个数。
例:
| 字符串 | 前缀 | 后缀 | 最长相等前后缀长度 |
|---|---|---|---|
| a | 空集 | 空集 | 0 |
| aa | a | a | 1 |
| aab | a、aa | b、ab | 0 |
| aaba | a、aa、aab | a、ba、aba | 1 |
| aabaa | a、aa、aab、aaba | a、aa、baa、abaa | 2 |
最长前缀用于判别可用于判别长度:
对某一子串,分别从从前缀首字符和后缀尾字符,向右(前缀)与向左(后缀)进行前缀和后缀的匹配,当发现所找到的前缀和后缀不相等时,之后再向左或向右进行匹配的字符串组合一定也是不相等,故此时便为最长公共前缀。
(4)前缀表
结合最长相等前后缀中所列的情况,便可得到前缀表,该表的意思是从左至右,依次选取字符子串,标记选取的字符子串所对应的最长相等前后缀的个数为多少。
例:

进行目标串的匹配:

在模式串匹配目标串过程中,当匹配到目标串中字符b时,由于与模式串的f不匹配,因此需要模式串右移进行重新匹配。
模式串将会根据当前不匹配的位置,查询该位置的前一个元素对应的前缀表中的值,进行跳转。
跳转原则:若当前字符不匹配,则在之前已匹配的字符子串中找到该子串所对应的最长公共前后缀,并将其跳转到对应位置。
即f处出错,则从f前的a a b a a查找最长相等前后缀,即 a a。然后就将模式串进行跳转。之后,便从 a a 后的 b开始与之前目标串不匹配的元素进行对比。
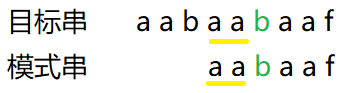
前缀表中的值,即为跳转的长度值。由于之前在比较到f时出错,aabaa时匹配,故从f前的字符对应的前缀表中获取跳转值,进行跳转。

next[i] = j的含义
-
当以next[0] = 0为起始时,next有两个含义:
(1)下标[0, i]构成的序列中,所具有的最长公共前后缀子序列长度为j,前缀子序列[0, j]与[i - j, i]相同。
(2)当遍历到下标为i+1的元素时,若出现不匹配,用next[i]中的下标所指向元素进行重新对比。 -
当以next[0] = -1为起始(相当于统一对1中的next减1),next的含义:
(1)下标[0, i]构成的序列中,所具有的最长公共前后缀子序列长度为j + 1,前缀子序列[0, j + 1]与[i - j - 1, i]相同。
(2)当遍历到下标为i的元素时,若出现不匹配,用next[i]中的下标所指向元素进行重新新对比。
参考视频:
帮你把KMP算法学个通透!(理论篇)
四、算法思想
KMP算法的核心思想就是使用字符串中已有的相同的子串信息,将这些信息记录下来,当再次进行比较时,不必再进行比较已记录过的相等部分,直接跳转到相等部分的下一位进行比较即可。
KMP的实现实际就是 跳过前方已相同的部分 进行对比,而为了能确定跳转的位置,就需要获取 最长相等的公共前后缀长度 。因此构造next数组的过程,就是获取 最长相等的公共前后缀长度 的过程并 完成长度和跳转位置的映射关系 。
双指针指向过程,在一个序列中,分别设置一个指向前缀子序列的尾端,另一个指向后缀子序列的尾端。每轮指向后缀子序列的指向向后遍历,每轮开始时,从之前已有的最长公共前后缀位置开始,这就需要前缀子序列尾指针指向已有的公共前后缀位置。后缀子序列在遍历时,每当找到一个前后缀相等的元素,前后缀的指针就一起向后移动一个位置,并根据此时最长公共前后缀长度在next中做记录。而遇到不相等的元素,则前缀指针不移动,后缀指针移动,并根据此时最长公共前后缀长度在next中做记录。
五、算法实现
分为两个部分,一个是构造next数组,即前缀表,一个是使用next数组将模式串与目标串进行匹配。
(1)构造next数组代码
next中不减去1
next中存储的为最长公共长度,因下标从0开始,因此长度减去1就等于跳转位置。
#includenext中减去1
next中存储的为长度减去一,也就是跳转的下标位置。
#include开始匹配,

遇到不相等,

j变为next[j - 1],
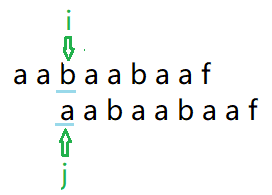
对比后依然不相等,而且j还为0,则记录next[i] = 0,将后移并进行下一轮的比较。

(2)使用next数组匹配目标串
next中不减去1
//const int M = 1e5 + 10, N = 1e6 + 10;
// int next[M];
// char p[M]; // 模式串
// char s[N]; // 目标串
// int m; // 模式串的长度
void getNext(int next[], char p[], int m){
// 初始化
next[0] = 0;
// j为前缀的末尾, i为后缀的末尾。前缀是除最后一个字符,后缀是除第一个字符。
for(int i = 1, j = 0; i < m; i++){
// 每次基于之前已记录的最长相等前后缀的基础上进行对比
// 处理前后缀不相同的情况,退回到之前最长的相等前后缀,基于此再进行延伸对比
while(j > 0 && p[i] != p[j]) j = next[j - 1]; // 存户的长度相对于下标少一个数,跳转时候根据next[j-1]跳转
// 处理前后缀相同的情况
if(p[i] == p[j]) j++;
// 在前缀表做记录
next[i] = j; // 存储最长相等前后缀的长度,而长度相对于下标少一个数,跳转时候根据next[i-1]跳转
}
}
void matching(int next[], char p[], int m, char s[], int n) {
int next[M];
getNext(next, p, m);
for(int i = 0, j = 0; i < n; i++){
// 每次基于已有最长公共前后缀匹配,处理不相同情况
while(j && s[i] != p[j]) j = next[j - 1];
// 处理相同情况
if(s[i] == p[j]) j++;
// 处理匹配成功情况
if(j == m)
// 输出目标串中所有与模式串匹配的起始位置下标
printf("%d ", i - m + 1);
// 为保证最长子序列匹配,因此从后向前进行匹配,将j指向前一个元素的next中的值
}
}
next中减去1
//const int M = 1e5 + 10, N = 1e6 + 10;
// int next[M];
// char p[M]; // 模式串
// char s[N]; // 目标串
// int m; // 模式串的长度
void getNext(int next[], char p[], int m){
// 初始化
next[0] = -1;
// j为前缀的末尾, i为后缀的末尾。前缀是除最后一个字符,后缀是除第一个字符。
for(int i = 1, j = -1; i < m; i++){
// 每次基于已有最长公共前后缀匹配,处理不相同情况
while(j >= 0 && p[i] != p[j + 1]) j = next[j]; // next中-1的好处是,跳转时候直接根据当前位置所记录的值跳转
// 处理前后缀相同的情况
if(p[i] == p[j + 1]) j++;
// 在前缀表做记录
next[i] = j; // 因初始化为-1,因此存储的值为最长相等前后缀的长度减去一
}
}
void matching(int next[], char p[], int m, char s[], int n) {
int next[M];
getNext(next, p, m);
for(int i = 0, j = -1; i < n; i++){
// 每次基于已有最长公共前后缀匹配,处理不相同情况
while(j >= 0 && s[i] != p[j]) j = next[j];
// 处理相同情况
if(s[i] == p[j + 1]) j++;
// 处理匹配成功情况
if(j == m - 1){ // j初始为-1,少一个数所以对比为n - 1
// 输出目标串中所有与模式串匹配的起始位置下标
printf("%d ", i - m + 1);
// 为保证最长子序列匹配,因此从后向前进行匹配,将j指向前一个元素的next中的值
// 还未匹配成功,跳转到待对比位置
j = next[j];
}
}
六、对应题目
题目描述
给定一个目标串 S,以及一个模式串 P,所有字符串中只包含大小写英文字母以及阿拉伯数字。
模式串 P在目标串 S中多次作为子串出现。
求出模式 P在目标串 S中所有出现的位置的起始下标。
输入格式
第一行输入整数 N,表示字符串 P的长度。
第二行输入字符串 P。
第三行输入整数 M,表示字符串 S的长度。
第四行输入字符串 S。
输出格式
共一行,输出所有出现位置的起始下标(下标从 0开始计数),整数之间用空格隔开。
数据范围
1≤N≤105
1≤M≤106
输入样例
3
aba
5
ababa
输出样例
0 2
代码实现
#include <stdio.h>
const int M = 1e5 + 10, N = 1e6 + 10;
void getNext(int m, char p[], int next[]){
next[0] = 0;
for(int j = 0, i = 1; i < m; i++){
while(j && p[i] != p[j]) j = next[j - 1];
if(p[i] == p[j]) j++;
next[i] = j;
}
}
int main(){
int n, m, next[M];
char p[M], s[N];
scanf("%d%s", &m, &p); // 构造字符串p
scanf("%d%s", &n, &s); // 构造字符串s
getNext(m, p, next);
for(int i = 0, j = 0; i < n; i++){
while(j > 0 && s[i] != p[j]) j = next[j - 1];
if(s[i] == p[j]) j++;
if(j == m){
printf("%d ", i - m + 1);
j = next[j - 1];
}
}
return 0;
}
时间复杂度为O(m + n),即模式串的长度+目标串的长度
参考视频:帮你把KMP算法学个通透!(求next数组代码篇)