【模电实验】基尔霍夫定律、叠加定理和戴维南定理验证实验
- 实验目的
- 验证基尔霍夫电流定律(KCL)和电压定律(KVL)加深对该定理的理解
- 验证叠加定理,加深对该定理的理解
- 验证戴维南定理,掌握有源二端口网络的开路电压,短路电流和入端等效电阻的测定方法
- 通过实验加强对参考方向的掌握和运用的能力
- 实验原理与说明
1.叠加定理:
对于一个具有唯一解的线性电路,由几个独立电源共同作用所形成的各支路电流或电压,是各个独立电源分别单独作用时在各相应支路中形成的电流或电压的叠加。
图1-1所示实验电路中有一个电压源Us及一个电流源Is。 设Us和Is共同作用在电阻RL、R3上产生的电流分别为IAB、IDB,如图1-1(a)所示。为了验证叠加原理令电压源和电流源分别作用。当电压源Us不作用,即Us=0时,在Us处用短路线代替;当电流源Is不作用,即Is=0时,在Is处用开路代替;而电源内阻都必须保留在电路中。
- 设电压源Us单独作用时(电流源支路开路)在电阻RL、R3上产生的电流分别为IAB‘、IDB‘
 ,如图1-1(b)所示。
,如图1-1(b)所示。 - 设电流源单独作用时(电压源支路短路)在电阻RL、R3上产生的电流分别为IAB‘’、IDB‘’
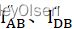 ,如图1-1(c)所示。
,如图1-1(c)所示。
这些电流的参考方向均已在图中标明。验证叠加定理,即验证式(1-1)成立。 IAB![]() = IAB‘+ IAB‘’
= IAB‘+ IAB‘’![]()
IDB![]() = IDB ‘+ IDB‘’
= IDB ‘+ IDB‘’![]() 式(1-1)
式(1-1)
2.基尔霍夫定律
1)基尔霍夫电流定律(KCL)
在任一时刻,流出(或流入)集中参数电路中任一节点的电流的代数和恒等于零,即: ΣI=0 或 ΣI入=ΣI出 式(1-2)
此时,若取流出节点的电流为正,则流入节点的电流为负。它反映了电流的连续性。说明了节点上各支路电流的约束关系,它与电路中元件的性质无关。
图1-1所示实验电路中要验证基尔霍夫电流定律,可选一电路节点B,按图中电流的参考方向测定出各支路电流值,并约定流出该节点的电流为正,反之取负号。将测得的各电流代入式(1-2),即:IS-IAB-IDB=0或IS=IAB+IDB加以验证。
2)基尔霍夫电压定律(KVL)
按约定的参考方向,在任一时刻,集中参数电路中任一回路上全部元件两端电压代数和恒等于零,即:ΣU=0 式(1-3)
它说明了电路中各段电压的约束关系,它与电路中元件的性质无关。式(1-3)中,通常规定凡支路或元件电压的参考方向与回路绕行方向一致者取正号,反之取负号。
图1-1所示实验电路中要验证基尔霍夫电压定律,可选电路右边回路,回路绕行方向为顺时针,按图中的参考方向测定出回路中各元件电压值,并约定与回路绕行方向一致者取正号,反之取负号,将测得的各电压代入式(1-3),,即:UAB+UBC+UCA=0加以验证。
3.电压、电流的实际方向与参考方向的对应关系
参考方向是为了分析、计算电路而人为设定的,如下图1-2所示。实验中测量的电压、电流的实际方向,由电压表、电流表的“正”端所标明。在测量电压、电流时,若电压表、电流表的“正”端与参考方向的“正”方向一致,则该测量值为正值,否则为负值。
4.戴维南定理
一个含独立电源,受控源和线性电阻的二端口网络,其对外作用可以用一个电压源串联电阻的等效电源代替,其等效源电压等于此二端口网络的开路电压,其等效内阻是二端口网络内部各独立电源置零后所对应的不含独立源的二端口网络的输入电阻(或称等效电阻)如图1-3所示。
5. 诺顿定理
一个含独立电源,受控源和线性电阻的二端口网络,其对外作用可以用一个电流源并联电阻的等效电源代替,其等效源电流等于此二端口网络的短路电流,其等效内阻是二端口网络内部各独立电源置零后所对应的不含独立源的二端口网络的输入电阻(或称等效电阻)如图1-4所示。
6. 有源二端网络等效参数的测量方法-----开路电压、短路电流法:
在有源二端网络输出端开路时,用电压表直接测量其输出端的开路电压Uoc,然后将输出端短路,用电流表测量其短路电流Isc,则等效电阻为
- 实验设备
名称 数量 型号
- 双路可调直流电源 1块 30121046
- 直流电压电流表 1块 30111047
- 电阻 4只 10W*1 330W*1 510W*2
- 测电流插孔 3只
- 电流插孔导线 3条
- 短接桥和连接导线 若干 P8-1和50148
- 实验用9孔插件方板 1块 300mm×298mm
- 可调电阻 1只 1000W*1
- 实验步骤
1. 实验电路如下图1-5所示,其中R1=330欧,R2= R3=510欧, R4=10欧, RL=400欧,稳压源的输出Es=12V,恒流源的输出Is=10mA。注意:应将稳压源调出相应的值再接入电路。恒流源接入电路中再调出相应的值。
分以下3种情况分别测量 Uab ,Ubc , Uca, Iab, Idb。将结果填入下表, 注意每次测量,读取数据时各支路电流及支路电压取关联参考方向。
1)令电压源、电流源共同作用。
2)令电压源单独作用。
3)令电流源单独作用
a.叠加原理的验证
根据表1-1测量的数据,通过计算分别验证Uab ,Ubc , Uca, Iab, Idb的值满足下面的叠加原理公式:
Y电压源、电流源共同作用=Y电压源单独作用+Y电流源单独作用
b. 基尔霍夫定律的验证
1)根据表1-1测量的数据,通过计算验证节点B的KCL方程: ΣI=0
2)根据表1-1测量的数据,通过计算验证回路ABC的KVL方程: ΣU=0
2. 戴维南、诺顿定理的验证
验证戴维南、诺顿定理的一个有源二端网络,如下图1-6(a)中虚线所示,其中R1=330欧,R2= R3=510欧, R4=10欧,用开路电压、短路电流法,测量该有源二端网络的开路电压Uoc和短路电流Isc,并计算R0,数据记录于表2中
(1)测量有源二端网络的外特性
在图1-6(a)所示电路中接入负载电阻RL(RL是由可变电阻组成的,使用前要先找准其零位,即RL=0的位置),改变RL的值,测量其两端电压和通过的电流,数据记录于表3中。
表3
| RL(Ω) |
0 |
200 |
400 |
600 |
800 |
1000 |
∞ |
| U(V) |
|||||||
| I(mA) |
(2)测量戴维南等效电路的外特性
构成戴维南等效电路如图1-6(b)所示(图中电压源Uoc和内阻R0为表2中测得的值,根据内阻R0的大小用实验箱中的510Ω、1Ω、2.2Ω、5.1Ω,10Ω等电阻串联在一起尽量接近R0的值(要求误差小于1Ω),;负载电阻RL仍用可变电阻器,改变RL的值,测量其两端电压和通过的电流,数据记录于表4中。
表4
| RL(Ω) |
0 |
200 |
400 |
600 |
800 |
1000 |
∞ |
| U(V) |
|||||||
| I(mA) |
(3) 测量诺顿等效电路的外特性
构成诺顿等效电路如图1-4(b)所示,图中电压源Isc和等效电阻R0为表2中测得的值,根据等效电阻Ro的大小用实验箱中的510Ω、1Ω、2.2Ω、5.1Ω,10Ω等电阻串联在一起, 尽量接近Ro的值(要求误差小于1Ω);负载电阻RL仍用可变电阻器),改变RL的值,测量其两端电压和通过的电流,数据记录于表5中。
表5
| RL(Ω) |
0 |
200 |
400 |
600 |
800 |
1000 |
∞ |
| U(V) |
|||||||
| I(mA) |
- 注意事项
- 测量电压、电位、电流时,不但要读出数值来,还要判断实际方向,并与设定的参考方向进行比较,若不一致,则该数前加“-”号。
- 注意稳压电源的输出端切勿短路,恒流源不可开路。
- 换接线路时,必须先关断电源。
- 实验完毕,须将导线、仪表归位,恢复到待使用状态。
- 分析和讨论
- 测量电压、电流时,如何判断数据前的正负号?负号的意义是什么?
- 电位出现负值,其意义是什么?
- 叠加原理、基尔霍夫定律和戴维南、诺顿定律分别在什么条件下成立?
- 在实验中,处理电压源和电流源的具体步骤和注意事项是什么?为什么?
- 实验报告要求
1.根据表1-1的测量数据,通过计算验证叠加定理和基尔霍夫定律的正确性。
2.电阻元件所消耗的功率能否用叠加原理计算而得,用实验数据通过计算结果说明。
3.根据表3、4、5的测量数据,在同一坐标纸上绘出各自的伏安特性曲线,比较其结果,以验证戴维南、诺顿定理及其等效变换的正确性。
4. 分析实验误差,总结实验收获和体会。
实验数据(仅供参考)





