MUTAN:Multimodal Tucker Fusion For Visual Question Answering
MUTAN:Multimodal Tucker Fusion For Visual Question Answering
0.写在前面
在介绍本篇论文前,我们首先介绍什么是矩阵分解,tucker张量分解,双线性模型??
0.1 矩阵分解
矩阵分解大致三个作用: 降维处理,稀疏数据填充,隐形关系挖掘。下面以推荐系统中常用的矩阵分解为例。
推荐系统中,给定一个大小为 m ∗ n m*n m∗n的评分矩阵R,元素 r i j r_{ij} rij表示用户i对商品j的评分值。
当R的秩 k = r a n k ( R ) < < m i n ( m , n ) k = rank(R)<
R = U V T R=UV^T R=UVT其中,U是大小为mxk的用户因子矩阵,V是nxk项因子矩阵,这一过程就是矩阵分解
当 k < r a n k ( R ) k
R ≈ U V T R \approx UV^T R≈UVT,U和V与前面含义相同,显然,整体误差为残差方程 R − U V T R-UV^T R−UVT中所有元素的平方和,即 ∣ ∣ R − U V T ∣ ∣ 2 ||R-UV^T||^2 ∣∣R−UVT∣∣2
在实际应用中,这里的R往往是一个稀疏矩阵,因为如果有1000个用户,1000个商品,构造评分矩阵,不需要每个用户把每个商品都买一遍??
矩阵分解在推荐系统中被称为隐性因子模型,定义用户i在环境c下对项j进行评分为 r i j c r_{ijc} rijc ,一个特殊的张量分解结构,即大小mxnxd的评分张量R分解会得大小为用户因子矩阵U:mxk,项因子矩阵V:nxk,环境因子矩阵W:dxk,这就是隐形因子模型的一种高阶泛化。
所以第3阶张量R上任意位置(i,j,c)所对应的评分计算如下:
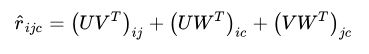
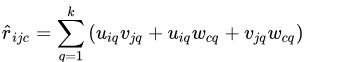
0.2 Tucker张量分解
张量分解有很多方法,张量分解通常用来解决稀疏张量的填补问题。
以三阶张量为例:假设张量 T = n 1 ∗ n 2 ∗ n 3 T=n_1*n_2*n_3 T=n1∗n2∗n3,则进行Tucker分解后变为
T ≈ X ∗ U ∗ V ∗ W T \approx X* U * V * W T≈X∗U∗V∗W

t i j k ≈ ∑ m = 1 r 1 ∑ n = 1 r 2 ∑ l = 1 r 3 ( x m n l ∗ u i m ∗ v j n ∗ w k l ) t_{ijk} \approx \sum_{m=1}^{r_1}\sum_{n=1}^{r_2}\sum_{l=1}^{r_3}(x_{mnl}*u_{im}*v_{jn}*w_{kl}) tijk≈m=1∑r1n=1∑r2l=1∑r3(xmnl∗uim∗vjn∗wkl)
其中 X : r 1 ∗ r 2 ∗ r 3 X:r_1*r_2*r_3 X:r1∗r2∗r3也就是核心张量,
U : n 1 ∗ r 1 , V : n 2 ∗ r 2 , W : n 3 ∗ r 3 U:n_1*r_1,V:n_2*r_2,W:n_3*r_3 U:n1∗r1,V:n2∗r2,W:n3∗r3
Tucker张量分解唯一性不能保证,因为可以在Tucker分解的各个因子矩阵上加上一些约束,例如正交约束,稀疏约束,平滑约束,非负约束等
0.3 双线性模型
双线性模型也有称为双线性池化,主要用于特征融合。
如果特征x和特征y来自两个特征提取器(例如VQA任务中,问题特征和图像特征),则被称为多模双线性池化(MBP),
如果来自同一个则交同源双线性池化(HBP)或者二阶池化。
原始的Bilinear Pooling存在融合后的特征维数过高的问题融合后的特征维数=特征x与特征y的维数乘积,一些论文作者尝试用PCA(主成分分析)进行降维,有的采用Tucker分解等
- 双线性池化
基于Bilinear CNN Models for Fine-grained Visual Recognition
![]()
它的双线性模型B由四个部分组成 B = ( f A , f B , P , C ) B=(f_A,f_B,P,C) B=(fA,fB,P,C), f A 和 f B f_A和f_B fA和fB是特征函数,P是池化函数,C是分类函数,公式如下:
它的公式如下:
![]()
公式理解:就是将图像中的同一位置上的两个特征进行乘,然后得到矩阵B,再对矩阵B进行sum pooliing池化得到矩阵 ξ \xi ξ,再对 ξ \xi ξ向量化,得到双线性向量x,再对x进行归一化操作,得到融合后的特征z,再将z用于分类和预测。
- 双线性模型
双线性模型指形如如下公式的操作:
![]()
忽视归一化操作,HBP特征如下表示:
![]()
把提取的特征送入全连接层再送入softmax层,公式等价是:
![]()
W j W_j Wj是全连接层的参数矩阵需要学习的, W j R W^R_j WjR是与之对应的,所以直接对 W j R W^R_j WjR进行学习。就是双线性模型与双线性池化差不多的原因。
- MLB(Mutimodal Low-rank Bilinear Pooliing)多模态低秩双线性池化方法
此概念出自《Hadamard product for low-rank bilinear pooling》,核心是Hadamard积(按元素乘)来实现bilinear model。把上面公式写成如下:
![]()
如果需要扩大矩阵 U i 和 V i U_i和V_i Ui和Vi,再采用了矩阵P,控制输出即可
![]()
- MCB(Multimodal Compact Bilinear Pooling)多模态紧凑型双线性池化
MCB在VQA任务中处理的过程如下:
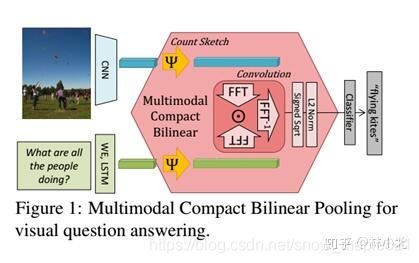

这里 Ψ \Psi Ψ是一个sketch函数(一种降维方式),![]()
![]()
MCB模块的工作:加了attention之后的框架如下:
![]()
这是一共用了两次的MCB模块,第一个融合了文本和图像的特征来提出图像的attention,第二个是将图像的attention特征与文本特征再一次融合,并将结构送入全连接网络,再送入softmax分类器得到答案。
本篇论文算是在双线性模型的融合上加了Tucker分解
1. 摘要
虽然Bilinear models(双线性模型)在VQA中能够很好的融合信息,帮助学习问题意义和图像内容之间的高级关联,但是存在高维度问题,所以本文引入MUTAN概念——基于多模态张量Tucker分解,能够有效的在视觉和文本的双线性交互(Bilinear models)的模型中进行参数化,除Tucker分解之外,还设计了基于矩阵的低秩分解 来明确限制交互等级。
2. 引言
VQA:是一种多模式任务,旨在回答有关图像的问题,要解决此问题,需要精确的图像和文本模型,并且这两种模式之间的高级交互必须仔细地编码到模型中才能提供正确的答案,而且该模型,必须具有理解整个场景的能力,以便将注意力放在与问题有关的区域,丢弃与问题无关的区域。
双线性模型:是VQA融合问题的有效方法,因为它编码了完整的二阶交互。这些双线性模型的主要问题与参数的数量有关,而参数数量相对于输入输出的维度就变得棘手,因此必须通过降低模型的复杂性来简化或近似双线性;
因此,解决这个问题,我们引入MUTNAN的新体系结构(图1),该体系主要就是对图像模型和问题模型的交互进行建模,采用的方法是基于Tucker分解,其能表示完整的双线性交互作用。
3. 相关工作
- 多模式视觉和文本的任务:主要是对空间特征图的对齐方式,
- 图像字幕任务:最新任务是旨在生成图像的语言描述。
- VQA任务:不是明确学习两个空间之间的对齐方式,而是合并两个模态以确定正确答案。
- 注意力机制:让模型更关注与问题有关的图像区域。本文采用【】文章中提供的注意力建模作为我们的整合工具关于我们针对全局融合和注意力建模的新融合策略。
- 融合策略:IMG+BOW模型是第一个使用及联合并全局图像表示和问题嵌入的模型,该问题嵌入是通过对问题中所学习的单词嵌入进行求和而获得的。
我们的工作:我们引入MUTAN——一种基于模态之间的双线性相互作用的多模态融合方案,在控制参数的数量上,MUTAN采用减少单峰嵌入的大小,同时使用完整的双线性融合方法来尽可能精确模拟它们之间的相互作用。
我们的贡献:
- 依靠基于Tucker张量的分解的VQA新融合方案,包括分解三个矩阵和一个核心张量
- 证明了Tucker分解框架,推广了最新的双线性模型,即使MCB和MLB具有更强大的表达能力。
- 结构稀疏性限制了核心张量,进一步控制模型参数数量,扮演着正则化的角色,防止了过度拟合。
3. MUTAN模型

图中描述:我们采用GRU递归网络对问题特征进行提取,采用全卷积神经网络Resnet来提取图像特征,再用T进行融合,产生向量y后再用softmax函数进行答案预测。我们MUTAN最终体系还嵌入了基于视觉注意力机制的方法。
- 融合与双线性模型(Fusion and Bilinear models):双线性模型是融合问题的最新有效解决方案,但是完全参数化的双线性相互作用在VQA中很难实现,因为GPU内存有限,所以在MUTAN中,我们使用Tucker分解对整个张量T进行分解,同时我们还建议构造第二张量Tc来完成分解。

3.1 Tucker decomposition(塔克分解)
3-way张量 T T T的塔克分解表示是因子矩阵 W v , W q , W o W_v,W_q,W_o Wv,Wq,Wo和核心张量 T c T_c Tc之间的张量积.

3.2 Multimodal Tucker Fusion(多峰塔克融合)
经过张量T的Tucker分解方程参数化张量T的权重时,y的输出可以这样表示:

这完全等同于将q和v的投影的完整双线性交互编码为一个潜在对表示z,并使用该潜在代码预测答案,如下:

将z再投影到预测空间,y就如下:

预测答案就是通过softmax后如下:
![]()
在本文实验中,我们的 q ~ , v ~ \tilde{q},\tilde{v} q~,v~如下计算:
符号注释:
- W q , W v W_q,W_v Wq,Wv:将问题和图像矢量投影到各个维 t q , t v t_q,t_v tq,tv的空间中, t q 或 t v t_q或t_v tq或tv维度越高,模型越复杂。
- T c T_c Tc:用于模拟 q ~ \tilde{q} q~和 v ~ \tilde{v} v~之间的相互作用。它从所有相关 q ~ \tilde{q} q~和 v ~ \tilde{v} v~到大小为 t o t_o to的z中学习投影。
- W o W_o Wo:对A中的每个类别的z对进行评分
3.2 Tensor sparsity
- 稀疏约束:
为什么引用稀疏约束?
有很多参数(特征)与我们的结果么有关系,或者是有些参数(特征)对我们的结果影响忽略不计。
如何做?
为了进一步在交互模型的表达性和复杂性之间取得平衡,我们基于Tc切片矩阵的秩引入了结构性的稀疏约束。当执行 q ~ \tilde{q} q~和 v ~ \tilde{v} v~的双线性组合时,z可以写成如下:

q ~ \tilde{q} q~和 v ~ \tilde{v} v~的相关性有 T c [ : , : , k ] T_c[:,:,k] Tc[:,:,k]的参数加权,每个切片中引入的结构可以用Tc切片上的等级约束来表示,我们给每个切片等级强加为常数R,每个切片 T c [ : , : , k ] T_c[:,:,k] Tc[:,:,k]则表示为R等级为1矩阵的和。如下:

那么 z [ k ] z[k] z[k]则表示:
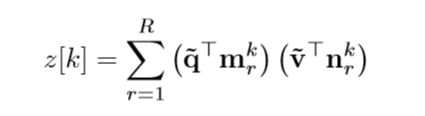
注释:
在 T c T_c Tc张量上加入秩的约束会导致将输出向量z表示为R个向量 z r z_r zr的总和。为了获得这些向量中的每一个,将 q ~ \tilde{q} q~和 v ~ \tilde{v} v~投影到一个公共空间,并将它们与元素乘积合并,因此可以将z解释为 q ~ \tilde{q} q~和 v ~ \tilde{v} v~的投影之间的多个and门,进行or交互建模, z [ k ] z[k] z[k]逻辑表达式则如下:
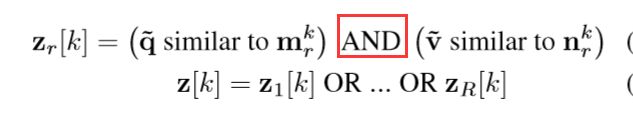
3.4 Model Unification and Discussion(模型统一与讨论)
我们将讨论如何将MCB和MLB作为我们Multimodal Tucker Fusion的特例,具体的如下图,彩色代表学习到的参数,灰色代表固定的参数。

3.4.1 Multimodal Compact Bilinear(MCB) 多峰紧凑双线性
核心张量Tc是稀疏的,遵循以下原则:

MCB中所有学习到的参数都是在融合后定位的。q和v的组合应该相互作用,它们事先被随机采样(通过h)。它们必须设置一个非常高的维数(通常为16000)。将这组组合作为特征向量进行分类。
3.4.2 Multimodal Low-rank Bilinear(MLB) 多峰低秩双线性
将Tucker简化为低秩分解时添加了两个约束:
- ①结构上 t q = t v = t o = R t_q=t_v=t_o=R tq=tv=to=R
- ②核心张量上:它被设置为恒等式。
q的维度k,仅被允许与它相同的维度v进行交互,我们将通过实验来展示消除这些约束后的效果。
MLB与张量稀疏Tensor Sparsity之间的差异主要在以下两种:
- ①我们在Tucker分解Tc的核心张量T上进行降秩,而在MLB中它们约束全局张量T的秩,使v,q维度不同
- ②我们没有在第三种模式上减少张量,而只是在对应与图像和问题模态的前两种模式上减少了张量。Tc中的隐式参数在mode-3 slice上相关,在slices之间独立
4. 实验
- MuTAN setup:
将(448x448)的图片经过ResNet152转换成14x14x2048特征图,当采用注意力机制时,保留14x14平铺,否则,图像将被表示为CNN输出的14x14矢量的平均值。采用GRU初始化预训练的Skip-thoughts模型的参数,采用ADAM训练模型。
4.1 融合方案比较
4.2 最新技术比较
- 注意力机制:采用[5],[8]介绍的多瞥注意力机制,采用MUTAN对问题向量的区域进行评分,并计算一个全局图像向量作为这些分数的加权的总和。
- Answer Sampling:答案子采样,10个真正的答案,在10个样本中,仅保留出现3次以上的答案,然后随机选择我们要求模型进行预测的答案。
- Ensembing: MUTAN(5)包含5个模型组合,3种注意力机制的MUTAN体系,和两种MLB的实例,可以看作是MUTAN的特例。
- Result 结果:

5.文献引用
| 文献名 | 年份 | 论文 |
|---|---|---|
| [5]:Multimodal compact bilinear pooling for visual question answering and visual grounding(用于视觉问题回答和视觉基础的多模态紧凑双线性池) | 2016 | https://arxiv.org/pdf/1606.01847v3.pdf |
| [6]:Deep residual learning for image recognition(图像识别的深度残差学习) | 2015 | https://arxiv.org/pdf/1512.03385v1.pdf |
| [7]:Multimodal Residual Learning for Visual QA(用于视觉QA的多模态残差学习) | 2016 | https://arxiv.org/pdf/1606.01455v2.pdf |
| [8]:Hadamard Product for Low-rank Bilinear Pooling(低秩双线性池的阿达玛积) | 2017 | https://arxiv.org/pdf/1610.04325v4.pdf |
| [10]:Multimodal neural language models(多模态神经语言模型) | 2014 | |
| [11]:Skip-thought vectors | 2015 | https://arxiv.org/pdf/1506.06726v1.pdf |
| [12]: Tensor decompositions and applications(张量分解及其应用) | 2009 | |
| [16]:Bilinear cnn models for fine-grained visual recognition (双线性cnn模型用于细粒度的视觉识别) | 2015 | |
| [17]:Hierarchical question-image co-attention for visual question answering分层问题-图像共同注意视觉问题回答). | 2016 | https://arxiv.org/pdf/1606.00061v5.pdf |
| [18]: Multimodal convolutional neural networks for matching image and sentence(用于图像和句子匹配的多模态卷积神经网络) | 2015 | https://arxiv.org/pdf/1504.06063v5.pdf |
| [21]:Exploring models and data for image question answering(为图像问题的回答探索模型和数据) | 2015 | https://arxiv.org/pdf/1505.02074v4.pdf |
| [27]: Ask, attend and answer: Exploring question-guided spatial attention for visual question answering(问、听、答:探索问题引导的空间注意,进行视觉的问题回答。) | 2016 | https://arxiv.org/pdf/1511.05234v2.pdf |
| [28]:Show, attend and tell: Neural image caption generation with visual attention (显示、出席和讲述:神经图像标题的生成和视觉关注) | 2015 | https://arxiv.org/pdf/1502.03044v3.pdf |
| [29]:Deep correlation for matching images and text(深度相关匹配图像和文本) | 2015 | |
| [30]: Stacked attention networks for image question answering(为图像问题回答堆叠注意力网络) | 2016 | https://arxiv.org/pdf/1511.02274v2.pdf |
致谢:
双线性模型介绍
张量分解




