【Java 数据结构】二叉树的遍历 (递归和非递归实现)

点进来你就是我的人了
博主主页：戳一戳,欢迎大佬指点!
人生格言：当你的才华撑不起你的野心的时候,你就应该静下心来学习!

欢迎志同道合的朋友一起加油喔
目标梦想：进大厂，立志成为一个牛掰的Java程序猿，虽然现在还是一个嘿嘿
谢谢你这么帅气美丽还给我点赞！比个心

---

目录

1.二叉树前序遍历

非递归思路:

遍历递归思路：在方法的外面new ，遇到合适的元素结点就给进放

子问题思路：将左边遍历完放进去，再遍历右边完放进去，也就是大问题变小问题

2.二叉树中序遍历

非递归思路:这道题与前面那道题相似，也是用栈实现,只是访问根节点的时机不同

遍历递归思路：在方法的外面new ，遇到合适的元素结点就给进放

子问题思路:

2.二叉树后序遍历

非递归思路:也是用栈实现,注意每次添加完一个结点后需要记录一下​编辑

遍历递归

子问题思路:

---

---

1.二叉树前序遍历

写题链接:力扣

非递归思路:

递归的执行时的函数栈帧就是递出去再回退, 如果要模拟递归, 一般情况下都是使用栈, 前序遍历(根, 左, 右)二叉树的非递归实现就是, 没有递归就只能用利用while循环

按照前线遍历的思路，在循环里头先添加根结点，然后不断往左遍历，直到左树为空，再继续遍历右树。从添加左树转为右树时，有个难点，右树可能为空，也可能不为空，如果右树为空,循环就直接结束了,我们没办法遍历剩下的元素了,所以我们需要要在外层再套上一个循环,当栈不为空时,从栈里面弹出一个元素继续遍历.

1.cur == null，如果栈也空了，那么说明全部结点已经添加完了，如果栈不为空，就继续弹出元素 tmp，使 cur 再次指向 tmp.right；

2.cur != null，继续进内层循环，不断添加元素，进而进行判断！！

   实现代码:

public List inorderTraversal(TreeNode root) {
        List ret = new ArrayList<>();
        if(root == null ) return ret;
        Stack stack = new Stack<>();
        TreeNode cur = root;
        while(cur != null || !stack.empty()) {
        while(cur != null) {
            stack.push(cur);
            cur = cur.left;
        } 
        TreeNode top = stack.pop();
        ret.add(top.val);
        cur = top.right;
        }
        return ret;
    }
}

遍历递归思路：在方法的外面new ，遇到合适的元素结点就给进放

class Solution {
    List ret = new ArrayList<>();
    public List preorderTraversal(TreeNode root) {
        if(root == null) return ret;   
        ret.add(root.val);
        preorderTraversal(root.left);
        preorderTraversal(root.right);
        return ret;   
    }
}

子问题思路：将左边遍历完放进去，再遍历右边完放进去，也就是大问题变小问题

    public List preorderTraversal(TreeNode root) {
        List ret = new ArrayList<>();
        if(root == null) return ret;   
        ret.add(root.val);
        List leftTree = preorderTraversal(root.left);
        ret.addAll(leftTree);
        List rightTree = preorderTraversal(root.right);
        ret.addAll(rightTree);
        return ret;   
    }

2.二叉树中序遍历

写题链接:力扣

非递归思路:这道题与前面那道题相似，也是用栈实现,只是访问根节点的时机不同

class Solution {
    public List inorderTraversal(TreeNode root) {
        List ret =new ArrayList<>();
        if(root == null ) {
            return ret;
        }
        TreeNode cur = root;
        Deque stack =new ArrayDeque<>();
        while(cur != null || !stack.isEmpty()){
        while(cur != null )  {
            stack.push(cur);
            cur =cur.left;
        }
        TreeNode top =stack.pop();
        ret.add(top.val);
        cur = top.right;
        }
        return ret;
    }
}

遍历递归思路：在方法的外面new ，遇到合适的元素结点就给进放

class Solution {
    List ret = new ArrayList<>();
    public List inorderTraversal(TreeNode root) {
    if(root == null) return ret;   
    inorderTraversal(root.left);
    ret.add(root.val);
    inorderTraversal(root.right);
    return ret;  
    } 
}

子问题思路:

class Solution {
    public List inorderTraversal(TreeNode root) {
        List ret = new ArrayList<>();
        if(root == null) return ret;   
        List leftTree = inorderTraversal(root.left);
        ret.addAll(leftTree);
        ret.add(root.val);
        List rightTree = inorderTraversal(root.right);
        ret.addAll(rightTree);
        return ret;   
    
    }
}

3.二叉树后序遍历

写题链接:力扣

非递归思路:也是用栈实现,注意每次添加完一个结点后需要记录一下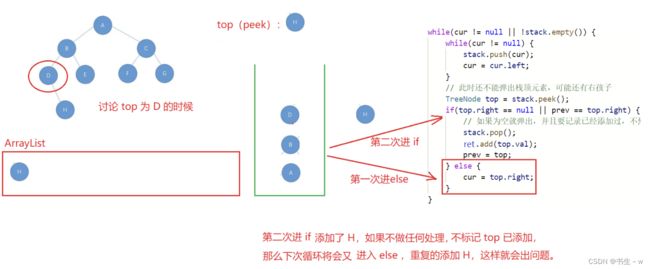

class Solution {
    // 主方法，实现后序遍历二叉树
    public List postorderTraversal(TreeNode root) {
        // 创建一个 List 用于存储后序遍历的结果
        List ret = new ArrayList<>();
        
        // 如果根节点为空，直接返回空结果
        if (root == null) return ret;
        
        // 创建一个栈用于存储待处理的节点
        Stack stack = new Stack<>();
        
        // 初始化 prev 为 null，用于记录前一个访问过的节点
        TreeNode prev = null;
        
        // 初始化 cur 为 root，表示当前处理的节点
        TreeNode cur = root;
        
        // 当 cur 不为空或栈不为空时，说明还有节点需要处理
        while (cur != null || !stack.empty()) {
            // 当 cur 不为空时，将其入栈，并将 cur 指向其左孩子
            while (cur != null) {
                stack.push(cur);
                cur = cur.left;
            }
            
            // 查看栈顶元素，但不弹出
            TreeNode top = stack.peek();
            
            // 如果 top 的右孩子为空或者已经被访问过，需要弹出 top 并将其值添加到结果列表中
            if (top.right == null || top.right == prev) {
                stack.pop();
                ret.add(top.val);
                // 更新 prev 为 top，表示已访问过 top 节点
                prev = top;
            } else {
                // 如果 top 的右孩子还未被访问过，将 cur 指向 top 的右孩子
                cur = top.right;
            }
        }
        
        // 返回后序遍历的结果
        return ret;
    }
}

遍历递归

class Solution {
    List ret = new ArrayList<>();
    public List postorderTraversal(TreeNode root) {
 
    if(root == null) return ret;   
    postorderTraversal(root.left);
    postorderTraversal(root.right);
    ret.add(root.val);
    return ret;   
    }
}

子问题思路:

class Solution {
    public List postorderTraversal(TreeNode root) {
        List ret = new ArrayList<>();
        if(root == null) return ret;   
        List leftTree = postorderTraversal(root.left);
        ret.addAll(leftTree);
        List rightTree = postorderTraversal(root.right);
        ret.addAll(rightTree);
        ret.add(root.val);
        return ret;   
    
    }
}