联发科 2024届 IC实习笔试分析

---

---

说明

记录一下  4月19日晚，发哥的一场笔试。分享给需要的 IC 人。

岗位：数字IC设计验证（安徽 合肥）

转载要经本人同意！

我的见解不一定都是准确的，欢迎评论区交流指正~~

---

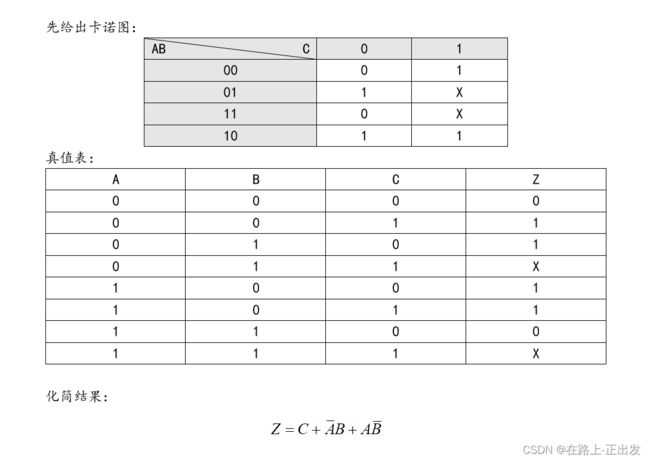
1、（20分）很经典的数电题目，请看：

这个数电题目只能说是很经典了；最关键的是处理约束项。

那么关于带约束项的化简，此处给出我的见解，供参考。

约束项的一般形式为：与或式  =  0 （如果不是此种形式，最好化为此种形式）；如此题的BC = 0；或者AB +CD = 0；ABC + CD = 0；等等。

直接求解的思路就是，画出卡诺图，把约束式等号左侧的各个与项对应的卡诺图格子画X，即无关项。对本题而言就是将BC（即B=1，且C=1）对应的格子画X。

下面给出具体求解：

 

2、（5分）简答题，ASIC flow 中综合工具的作用是什么？综合的时候需要SDC文件进行约束，请列举3条SDC的语法。

给出我的见解：综合的作用就是将 HDL 代码映射为期间库中的门级网表。

SDC语法列举：

set_input_delay delay_value -clock clock_ref [–max] [–min] [–clock_fall] [-rise] [-fall] [-add_delay] input_list

create_clock[-add] [-name ] -period [-waveform]

set_false_path -from [get_clocks CLKA]-to [get_clocks CLKB]]

3、（10分）智力题（推理题）

文字太烦，本人直接放弃。给大家看看：

（1）2 12 1112 3112 132112 ，问你下一个数是啥？给理由；

 

（2）有一个小偷费劲力气进入到了银行的金库里。在金库里他找到了一百个箱子，每一个箱子里都装满了金币。不过，只有一个箱子里装的是真的金币，剩下的99个箱子里都是假的。真假金币的外形和质感完全一样，任何人都无法通过肉眼分辨出来。它们只有一个区别：真金币每一个重量为101克，而假金币的重量是100克。在金库里有一个电子秤，它可以准确地测量出任何物品的重量，精确到克。但很不幸的是，这个电子秤和银行的报警系统相连接，只要被使用一次就会立刻失效。请问，小偷怎么做才能只使用一次电子秤就找到装着真金币的箱子呢?

这个题目很经典：

 4、（10分）选择参与过的任一个项目，简述项目内容以及流程，讲述您在项目中承担的任务，挑一项你认为难的地方并阐述解决方案。

5、（5分）用python写一个冒泡排序的函数以及测试程序。

def bubbleSort(arr):
    n = len(arr)
 
    # 遍历所有数组元素
    for i in range(n):
 
        # Last i elements are already in place
        for j in range(0, n-i-1):
 
            if arr[j] > arr[j+1] :
                arr[j], arr[j+1] = arr[j+1], arr[j]
 
arr = [64, 34, 25, 12, 22, 11, 90]
 
bubbleSort(arr)
 
print ("排序后的数组:")
for i in range(len(arr)):
    print ("%d" %arr[i]),

6、（15分）用Verilog 写一个 Round Robin 仲裁器。模块端口如下：

input clock;

input reset_b;

input [N-1:0] request;

input [N-1] lock;

output [N-1] grant; //one-hot

此处的 lock 输入信号，表示请求方收到了仲裁许可，在对应的lock拉低之前，仲裁器不可以开启新的仲裁。（可简单理解为仲裁器占用）

该题要求参数化编程，在模块例化时可调整参数。也即是说你不能写一个固定参数，比如N=8的模块。

参考波形图：

此题的思路参考：

Round-Robin算法的verilog实现  

结合题目的需求，我在这里给出我的见解：

设计源码：

// ===================================================================================
// 功能：
// 		-1- Round Robin 仲裁器
//      -2- 仲裁请求个数N可变
// 		-3- 加入lock机制（类似握手）
// 		-4- 复位时的最高优先级定为 0 ，次优先级：1 -> 2 …… -> N-2 -> N-1
// By：Xu Y. B.
// ===================================================================================

`timescale 1ns / 1ps
module Round_Robin_Arbiter #(
parameter 		N 		= 		4 //仲裁请求个数
)(
input 							clock,
input 							reset_b,
input 			[N-1:0]			request,
input 			[N-1:0]			lock,
output reg 		[N-1:0] 		grant//one-hot
    );
// 模块内部参数

localparam LP_ST_IDLE      		 = 3'b001;// 复位进入空闲状态，接收并处理系统的初次仲裁请求
localparam LP_ST_WAIT_REQ_GRANT  = 3'b010;// 等待后续仲裁请求到来,并进行仲裁
localparam LP_ST_WAIT_LOCK 		 = 3'b100;// 等待LOCK拉低

// 模块内部信号
reg [2:0]   R_STATUS;
reg [N-1:0] R_MASK;
wire [N-1:0] W_REQ_MASKED;

assign W_REQ_MASKED = request & R_MASK;

always @ (posedge clock)
begin
	if(~reset_b)
	begin
		R_STATUS <= LP_ST_IDLE;
		R_MASK <= 0;
		grant <= 0;
	end
	else
	begin
		case(R_STATUS)
		LP_ST_IDLE:
		begin
			if(|request) //首次仲裁请求
			begin
				R_STATUS <= LP_ST_WAIT_LOCK;
				grant <= request & ((~request)+1);
				R_MASK <= ~((request & ((~request)+1))-1 | (request & ((~request)+1)));	
			end
			else
			begin
				R_STATUS <= LP_ST_IDLE;
			end
		end     
		LP_ST_WAIT_REQ_GRANT://处理后续的仲裁请求
		begin
			if(|request)
			begin
				R_STATUS <= LP_ST_WAIT_LOCK;
				if(|(request & R_MASK))//不全为零
				begin
					grant <= W_REQ_MASKED & ((~W_REQ_MASKED)+1);
					R_MASK <= ~((W_REQ_MASKED & ((~W_REQ_MASKED)+1))-1 | (W_REQ_MASKED & ((~W_REQ_MASKED)+1)));
				end
				else
				begin
					grant <= request & ((~request)+1);
					R_MASK <= ~((request & ((~request)+1))-1 | (request & ((~request)+1)));
				end
			end
			else
			begin
				R_STATUS <= LP_ST_WAIT_REQ_GRANT;			
				grant <= 0;			
				R_MASK <= 0;			
			end
		end   
		LP_ST_WAIT_LOCK:
		begin
			if(|(lock & grant)) //未释放仲裁器		
			begin		
				R_STATUS <= LP_ST_WAIT_LOCK;		
			end		
			else if(|request) //释放的同时存在仲裁请求		 
			begin		
				R_STATUS <= LP_ST_WAIT_LOCK;
				if(|(request & R_MASK))//不全为零
				begin
					grant <= W_REQ_MASKED & ((~W_REQ_MASKED)+1);
					R_MASK <= ~((W_REQ_MASKED & ((~W_REQ_MASKED)+1))-1 | (W_REQ_MASKED & ((~W_REQ_MASKED)+1)));
				end
				else
				begin
					grant <= request & ((~request)+1);
					R_MASK <= ~((request & ((~request)+1))-1 | (request & ((~request)+1)));
				end		
			end
			else
			begin
				R_STATUS <= LP_ST_WAIT_REQ_GRANT;
				grant <= 0;			
				R_MASK <= 0;
			end		
		end		
		default:		
		begin
			R_STATUS <= LP_ST_IDLE;
			R_MASK <= 0;
			grant <= 0;
		end
		endcase
	end
end
endmodule

仿真文件：

// =====================================================================
// 功能：测试模块 Round_Robin_Arbiter 功能 
// By：Xu Y. B.
// =====================================================================

`timescale 1ns / 1ps
module TB_Round_Robin_Arbiter();

parameter 		N 		= 		4; //仲裁请求个数

reg 							clock;
reg 							reset_b;
reg 			[N-1:0]			request;
reg 			[N-1:0]			lock;
wire 			[N-1:0] 		grant;//one-hot

initial clock = 0;
always #10 clock = ~clock;

initial
begin
	reset_b <= 1'b0;
	request <= 0;
	lock <= 0;
	#20;
	reset_b <= 1'b1;
	@(posedge clock)
	request <= 2;
	lock <= 2;

	@(posedge clock)
	request <= 0;

	@(posedge clock)
	request <= 5;
	lock <= 7;

	@(posedge clock)
	lock <= 5;

	@(posedge clock)
	request <= 1;

	@(posedge clock)
	lock <= 1;

	@(posedge clock)
	request <= 0;

	@(posedge clock)
	lock <= 0;

	#100;
	$finish;
end

Round_Robin_Arbiter #(
		.N(N)
	) inst_Round_Robin_Arbiter (
		.clock   (clock),
		.reset_b (reset_b),
		.request (request),
		.lock    (lock),
		.grant   (grant)
	);

endmodule

仿真结果：

 对比给的参考波形，二者一致。

7、（15分）关于DMA寄存器配置，DMA寄存器（地址 0x81050010）表：

Type 表示读写类型。Reset 表示复位值。

写一个C函数 void dma_driver(void)，按步骤完成以下需求：

• 分配DMA所需的源地址（0x30）
• 分配DMA所需的目的地址（0x300）
• 设置传输128 Byte 数据
• 开始DMA传输
• 等待DMA传输结束

代码写法不唯一，这里给出我的见解：

void dma_driver(void)
{
	unsigned int *prt = (unsigned int *)0x81050010;
	int DMA_SRC_ADDR = 0x30;
	int DMA_DST_ADDR = 0x300;
	int DMA_LENGTH = 128;
	int DMA_START = 0X01;

	// STEP1
	*prt |= DMA_SRC_ADDR << 2; 
	// STEP2
	*prt |= DMA_DST_ADDR << 13; 
	// STEP3
	*prt |= DMA_LENGTH << 24; 
	// STEP4	
	*prt |= DMA_START; 

	while((*prt) & DMA_START)
	{

	}
}

8、（20分）二阶带通滤波器，利用RC组件搭建，通带范围 1kHz~30kHz ，两个电阻 R 均为10kΩ ，问两个电容容值多少？

首先你得知道二阶带通（RC）滤波器的电路长啥样：

 

基本思路就是计算传输函数，然后找截止频率；由于R1=R1=10kΩ，所以公式推导时均用R表示：（如发现推导步骤有问题，请及时在评论区留言，谢谢）

 根据最后推导得到的表达式，对于 jwRC2 ，这一项，当 w 趋于无穷大时，uo/ui 趋于零。那么高频的临界点就是 wRC2 = 1+2C2/C1；（此时忽略低频项 1/jwRC1） ；

同理，对于低频项 1/jwRC1， w 趋于无穷小时，uo/ui 趋于零 ，那么低频的临界点就是   1/wRC1 = 1+2C2/C1；

整理：

 

求解过程用到了MATLAB：

 

思路参考自： RC频率滤波电路设计

至此，发哥19日晚的笔试题目全部整理完毕，如有问题，请及时告知（评论区留言吧~~）

IC 加油！