LeetCode腾讯50题-Day8-62/70/78

LeetCode50题（17天）-Day8

62 不同路径

• 题号：62
• 难度：中等
• https://leetcode-cn.com/problems/unique-paths/

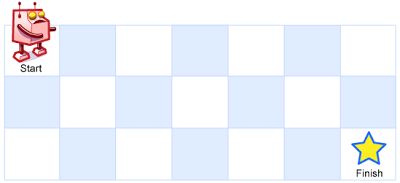
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

例如，上图是一个7 x 3 的网格。有多少可能的路径？

说明：m 和 n 的值均不超过 100。

示例 1:

输入: m = 3, n = 2
输出: 3
解释:
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右

示例 2:

输入: m = 7, n = 3
输出: 28

示例 3:

输入: m = 23, n = 12
输出: 193536720

---

实现

第一种：利用递归

public class Solution
{
    private int _m;
    private int _n;
    public int UniquePaths(int m, int n)
    {
        _m = m;
        _n = n;
        int count = 0;
        RecordPaths(0, 0, ref count);
        return count;
    }
    private void RecordPaths(int i, int j, ref int count)
    {
        if (i == _m - 1 && j == _n - 1)
        {
            count++;
            return;
        }
        if (i < _m)
        {
            RecordPaths(i + 1, j, ref count);
        }
        if (j < _n)
        {
            RecordPaths(i, j + 1, ref count);
        }
    }
}

使用递归的方式，容易理解但会耗费大量的时间，所以在运行 示例3 的时候，超时了。

第二种：利用动态规划

动态规划表格01：

动态规划表格02：

动态规划的最优子结构为：d[i,j] = d[i-1,j] + d[i,j-1]

• 状态：通过
• • 执行用时: 48 ms, 在所有 C# 提交中击败了55.84% 的用户
• 内存消耗: 14.7 MB, 在所有 C# 提交中击败了 88.33% 的用户

public class Solution
{
    public int UniquePaths(int m, int n)
    {
        int[,] memo = new int[m, n];
        for (int i = 0; i < m; i++)
        {
            for (int j = 0; j < n; j++)
            {
                if (i == 0)
                {
                    memo[i, j] = 1;
                }
                else if (j == 0)
                {
                    memo[i, j] = 1;
                }
                else
                {
                    memo[i, j] = memo[i - 1, j] + memo[i, j - 1];
                }
            }
        }
        return memo[m - 1, n - 1];
    }
}

70 爬楼梯

• 题号：70
• 难度：简单
• https://leetcode-cn.com/problems/climbing-stairs/

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：

输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
1.  1 阶 + 1 阶
2.  2 阶

示例 2：

输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1.  1 阶 + 1 阶 + 1 阶
2.  1 阶 + 2 阶
3.  2 阶 + 1 阶

示例 3：

输入： 44
输出： 1134903170

---

实现

分析这个题目：

• 1 阶，f(1) = 1 种方案
• 2 阶，f(2) = 2 种方案
• 3 阶，f(3) = 3 种方案
• 4 阶，f(4) = 5 种方案
• ……
• n 阶，f(n) = f(n-1) + f(n-2) 种方案

即，该问题可以转换为斐波那契数列问题。

第一种：利用递归

public class Solution {
    public int ClimbStairs(int n) {
        if (n <= 2)
            return n;

        return ClimbStairs(n - 1) + ClimbStairs(n - 2);        
    }
}

由于递归的执行速度，远远小于循环，导致“超出时间限制”。

第二种：利用循环

• 状态：通过
• 45 / 45 个通过测试用例
• 执行用时: 52 ms, 在所有 C# 提交中击败了 97.87% 的用户
• 内存消耗: 13.7 MB, 在所有 C# 提交中击败了 5.98% 的用户

public class Solution {
    public int ClimbStairs(int n) {
        if (n <= 2)
            return n;

        int first = 1;
        int second = 2;
        int result = 0;

        for (int i = 3; i <= n; i++)
        {
            result = first + second;
            first = second;
            second = result;
        }
        return result;        
    }
}

78 子集

• 题号：78
• 难度：中等
• https://leetcode-cn.com/problems/subsets/

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:

输入: nums = [1,2,3]
输出:
[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

---

实现

第一种：回溯法

依次以nums[i]为启始点进行搜索，且后续搜索数值都要大于前一个数值，这样会避免重复搜索。

• 状态：通过
• 10 / 10 个通过测试用例
• 行用时: 356 ms, 在所有 C# 提交中击败了 92.31% 的用户
• 内存消耗: 29.2 MB, 在所有 C# 提交中击败了 6.67% 的用户

public class Solution
{
    private IList<IList<int>> _result;
    
    public IList<IList<int>> Subsets(int[] nums)
    {
        _result = new List<IList<int>>();
        int len = nums.Length;

        if (len == 0)
        {
            return _result;
        }
        IList<int> item = new List<int>();
        Find(nums, 0, item);
        return _result;
    }

    private void Find(int[] nums, int begin, IList<int> item)
    {
        // 注意：这里要 new 一下
        _result.Add(new List<int>(item)); 

        if (begin == nums.Length)
            return;

        for (int i = begin; i < nums.Length; i++)
        {
            item.Add(nums[i]);
            Find(nums, i + 1, item);

            // 组合问题，状态在递归完成后要重置
            item.RemoveAt(item.Count - 1); 
        }
    }
}

第二种：子集扩展法

• 状态：通过
• 10 / 10 个通过测试用例
• 执行用时: 352 ms, 在所有 C# 提交中击败了 94.51% 的用户
• 内存消耗: 29.2 MB, 在所有 C# 提交中击败了 6.67% 的用户

public class Solution
{
    public IList<IList<int>> Subsets(int[] nums)
    {
        IList<IList<int>> result = new List<IList<int>>();
        IList<int> item = new List<int>();
        result.Add(item);
        for (int i = 0; i < nums.Length; i++)
        {
            for (int j = 0, len = result.Count; j < len; j++)
            {
                item = new List<int>(result[j]);
                item.Add(nums[i]);
                result.Add(item);
            }
        }
        return result;
    }
}

第三种：位运算

思路： 利用整数集合的思路。

以{1,2,3}为例，三个数，共2^3个子集。

000 -> []
100 -> [1]
101 -> [1,3]
110 -> [1,2]
111 -> [1,2,3]
...

C# 语言

• 状态：通过
• 10 / 10 个通过测试用例
• 执行用时: 348 ms, 在所有 C# 提交中击败了 97.80% 的用户
• 内存消耗: 29.5 MB, 在所有 C# 提交中击败了 6.67% 的用户

public class Solution
{
    public IList<IList<int>> Subsets(int[] nums)
    {
        IList<IList<int>> result = new List<IList<int>>();
        int count = nums.Length;

        for (int i = 0; i < 1 << count; i++)
        {
            IList<int> item = new List<int>();
            for (int j = 0; j < count; j++)
            {
                int mask = 1 << j;
                if ((mask & i) != 0)
                    item.Add(nums[j]);
            }
            result.Add(item);
        }
        return result;
    }
}

Python 语言

• 执行结果：通过
• 执行用时：40 ms, 在所有 Python3 提交中击败了 63.08% 的用户
• 内存消耗：13.8 MB, 在所有 Python3 提交中击败了 5.72% 的用户

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        count = len(nums)
        result = []
        for i in range(1 << count):
            item = []
            for j in range(count):
                mask = 1 << j
                if (mask & i) != 0:
                    item.append(nums[j])
            result.append(item)
        return result