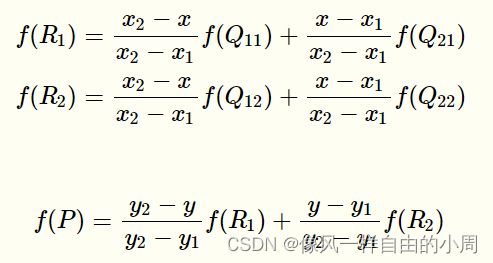常见的上采样操作以及其Pytorch实现

常见的上采样操作以及其Pytorch实现

整理一下常见的上采样操作，主要有线性插值、反卷积、sub-pixel Convolution等

一、插值

插值方法主要分为最近临插值、双线性插值、双三次插值 。

1.最近邻插值

最近邻插值选取与待填充位置最近的像素值作为该位置的值。Pytorch代码如下：

import torch
import torch.nn as nn

input = torch.arange(1, 5, dtype=torch.float32).view(1, 1, 2, 2)
print(input)

tensor([[[[1., 2.],
          [3., 4.]]]])
# 最近邻插值
nearest_interpolation = nn.UpsamplingNearest2d(scale_factor=2)
print(nearest_interpolation(input))

tensor([[[[1., 1., 2., 2.],
          [1., 1., 2., 2.],
          [3., 3., 4., 4.],
          [3., 3., 4., 4.]]]])

官方介绍如下：

2.双线性插值

最近邻插值虽然简单，但是会带来明显的棋盘效应以及演示网页。

假设反卷积生成的图像中，包含1只黑猫，黑猫身体部分的像素颜色应该是平滑过渡的。或者极端的说，身体部分应该全部都是黑色的。而在实际生成的图像中，该部分却是由深深浅浅的近黑方块组成的，很像棋盘的网络。这就是所谓的棋盘效应。现在显著性检测还存在的一个问题就是，在像素级的视觉任务中，会出现这个棋盘效应。这个效应在深度卷积神经网络中的影响是很大的。比如：如果在FCN的输出中出现这个效应，那么这个网络的训练就有可能失败，并且结果完全错误。而这些效应出现的源头就是上采样机制，一般出现在反卷积中。就是在反卷积过程中，当卷积核大小不能被步长整除时，反卷积就会出现重叠问题，插零的时候，输出结果会出现一些数值效应，就像棋盘一样。

最近邻插值的一个改进算法是双线性插值。计算算法如下，其中$P为待计算元素,Q_{11}、Q_{12}、Q_{21}、Q_{22}代表与P最相邻的四个元素$。计算公式如下：

Pytorch实现如下：

# 双线性插值
Bilinear_interpolation = nn.UpsamplingBilinear2d(scale_factor=2)
print(Bilinear_interpolation(input))

tensor([[[[1.0000, 1.3333, 1.6667, 2.0000],
          [1.6667, 2.0000, 2.3333, 2.6667],
          [2.3333, 2.6667, 3.0000, 3.3333],
          [3.0000, 3.3333, 3.6667, 4.0000]]]])

官方文档介绍如下：

3.双三次插值

这个算法计算过程有点复杂，这里不再详细论述。

Pytorch代码如下，其中mode 可使用的上采样算法，有nearest, linear, bilinear ，bicubic and trilinear. 默认使用 nearest：

Bicubic_interpolation = nn.Upsample(scale_factor=2, mode='bicubic', align_corners=True)
print(Bicubic_interpolation(input))

tensor([[[[1.0000, 1.3148, 1.6852, 2.0000],
          [1.6296, 1.9444, 2.3148, 2.6296],
          [2.3704, 2.6852, 3.0556, 3.3704],
          [3.0000, 3.3148, 3.6852, 4.0000]]]])

Bicubic_interpolation = nn.Upsample(scale_factor=2, mode='bicubic', align_corners=False)
print(Bicubic_interpolation(input))

tensor([[[[0.6836, 1.0156, 1.5625, 1.8945],
          [1.3477, 1.6797, 2.2266, 2.5586],
          [2.4414, 2.7734, 3.3203, 3.6523],
          [3.1055, 3.4375, 3.9844, 4.3164]]]])

官方文档介绍如下：

二、反卷积

好了，接下来就是利用深度学习算法来进行上采样了。反卷积又叫转置卷积，这里推荐一个简短的介绍反卷积工作原理的视频。简单地说，反卷积就是先往图像或特征图上填充很多的0，然后利用正常卷积去卷。

反卷积是一种特殊的卷积，总是可以使用一种卷积来模拟反卷积的过程。然而该方式将引入许多‘0’的行和‘0’的列，导致实现上非常的低效。并且，反卷积只能恢复尺寸，并不能恢复数值，因此经常用在神经网络中作为提供恢复的尺寸，具体的数值往往通过训练得到。此外，反卷积有一个严重的问题就是棋盘效应（上面双线性插值介绍过）。常见的解决棋盘效应的做法为先插值Resize再卷积。

Pytorch代码如下：

Transposed = nn.ConvTranspose2d(1, 1, 3, stride=1, padding=0)
print(Transposed(input))

tensor([[[[ 0.2539,  0.7710,  0.4962, -0.2961],
          [ 0.5497,  1.3513,  0.5077, -0.2974],
          [-0.0971, -0.7856, -0.6271,  0.6010],
          [ 0.6732,  0.5091, -0.6448, -0.2129]]]],
       grad_fn=<ConvolutionBackward0>)

官方文档介绍如下：

三、sub-pixel Convolution

普通的上采样采用的临近像素填充算法，主要考虑空间因素，没有考虑channel因素，上采样的特征图人为修改痕迹明显，图像分割与GAN生成图像中效果不好。为了解决这个问题，ESPCN中提到了亚像素上采样方式。具体原理如下：

这种操作能够将原来维度为$B\times C\times H\times W$变成$B\times C\times sH\times sW$。主要过程分为两步：

• 先通过几个正常卷积层将维度从$B\times C\times H\times W$变成 $B\times sC\times H\times W$
• 然后通过Pixel Shuffle操作将维度从$B\times sC\times H\times W$变成 $B\times C\times sH\times sW$

Pixel Shuffle的主要功能就是将这 $s^2$ 个通道的特征图组合为新的的 $B\times C\times sH\times sW$上采样结果。具体来说，就是将原来一个低分辨的像素划分为$s^2$ 个更小的格子，利用 $s^2$ 个特征图对应位置的值按照一定的规则来填充这些小格子。按照同样的规则将每个低分辨像素划分出的小格子填满就完成了重组过程。在这一过程中模型可以调整 $s^2$ 个shuffle通道权重不断优化生成的结果。

卷积的Pytorch实现不用多说，关于Pixel Shuffle的实现Pytorch已经可以直接调用类，如下：

pixel_shuffle = nn.PixelShuffle(3) # 这里的3就是s
input = torch.randn(1, 9, 4, 4)
output = pixel_shuffle(input)
print(output.size())

torch.Size([1, 1, 12, 12]) # 可以看到通道数变小s²倍，长宽分别扩大s倍

官方文档介绍如下：

四、其它方法

1.superpoint使用方法

上面的Interest Point Decoder使用的是将特征图reshape操作，和上面的Pixel Shuffle类似，都是将维度从$B\times sC\times H\times W$变成 $B\times C\times sH\times sW$。这里代码就不再展示了就是用来reshape和permute（维度变化）。

Descriptor Decoder使用的是三线性插值。

2.待补充