NSSCTF Round#11 --- 密码个人赛 wp
文章目录
-
-
- ez_enc
- MyMessage
- MyGame
- ez_signin
- ez_fac
-
ez_enc
题目:
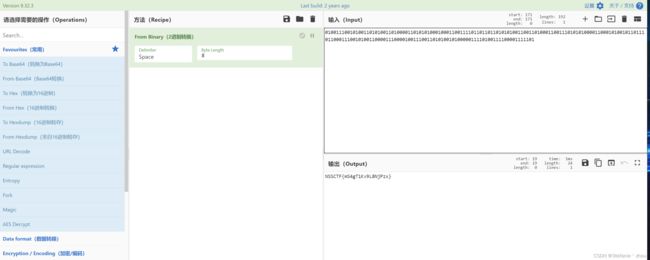
ABAABBBAABABAABBABABAABBABAAAABBABABABAAABAAABBAABBBBABBABBABBABABABAABBAABBABAAABBAABBBABABABAAAABBAAABABAABABBABBBABBAAABBBAABABAABBAAAABBBAAAABAABBBAABBABABAABABAAAAABBBBABAABBBBAAAABBBBBAB
将A替换为0,B替换为1,再二进制转字符串
NSSCTF{mS4gT1Kv9L8NjPzx}
MyMessage
题目:
from Crypto.Util.number import *
import os
flag = os.getenv('FLAG')
e = 127
def sign():
msg = input("Input message:")
p = getPrime(512)
q = getPrime(512)
n = p*q
c = pow(bytes_to_long((msg + flag).encode()), e, n)
print(f"n: {n}")
print(f"Token: {hex(c)}")
def main():
while True:
sign()
main()
与黄河流域警校CTF类似,取127组数据构成 低加密指数广播攻击,之后按照板子解题即可
解题代码:
import gmpy2
from pwn import *
from functools import reduce
from Crypto.Util.number import *
def CRT(ai, mi):
assert (reduce(gmpy2.gcd, mi) == 1)
assert (isinstance(mi, list) and isinstance(ai, list))
M = reduce(lambda x, y: x * y, mi)
ai_ti_Mi = [a * (M // m) * gmpy2.invert(M // m, m) for (m, a) in zip(mi, ai)]
return reduce(lambda x, y: x + y, ai_ti_Mi) % M
e = 127
n = []
c = []
for i in range(127):
p = remote('node2.anna.nssctf.cn', 28949)
message='1'
send_data = p.sendline(message.encode())
get_n = p.recvline().decode()
get_token = p.recvline().decode()
n_data = int(get_n.split(':')[1].replace('\n',''))
c_data = int(get_token.split(':')[1].strip(),16)
n.append(n_data)
c.append(c_data)
M = int(CRT(c,n))
m = gmpy2.iroot(M,127)[0]
flag = long_to_bytes(m)
print(flag)
MyGame
题目:
from Crypto.Util.number import *
import os
import random
import string
flag = os.getenv('FLAG')
def menu():
print('''=---menu---=
1. Guess
2. Encrypt
''')
p = getPrime(512)
q = getPrime(512)
n = p*q
def randommsg():
return ''.join(random.choices(string.ascii_lowercase+string.digits, k=30))
mymsg = randommsg()
def guess():
global mymsg
msg = input()
if msg == mymsg:
print(flag)
else:
print(mymsg)
mymsg = randommsg()
def encrypt():
e = random.getrandbits(8)
c = pow(bytes_to_long(mymsg.encode()), e, n)
print(f'Cipher_{e}: {c}')
def main():
print(f'n: {n}')
while True:
opt = int(input())
if opt == 1:
guess()
elif opt == 2:
encrypt()
main()
显然n已经确定了,那么直接取两组数据构成共模攻击,然后按照板子解题即可
解题代码:
from Crypto.Util.number import *
import gmpy2
def egcd(a, b):
if a == 0:
return (b, 0, 1)
else:
g, y, x = egcd(b % a, a)
return (g, x - (b // a) * y, y)
def deocode():
n = 92376669002623921509402142523040417979742847285128913230222037277281193123569384917422295565460337201247419578329317570919388466167460921476436708744255861919569840646055365622736782018449981456970295507042507578400203506466228792516604670880411611388070363010575761687416199559859671498479577162814750167227
c1 = 56209807203263700238616560618292167910103178762773040784631746817419178047868684355927134794504437622277771565804770934927080520866774097937077159522561456694970573720502644960107683432027702982653269325018244743399259436663458302138397221829147003127560773174189067496942399020628208697090961657373400555014
c2 = 90201008191161333080317628432839944522494767331025005565907527059217108167006947509077285590701267614286437629784262846613850046677772564536135707131060135969549898546289759735024482099701063980172806975932382772513818194522857561088504530894222162124688966716463702313948548512256262573687696646070994545974
e1 = 170
e2 = 98
s = egcd(e1, e2)
s1 = s[1]
s2 = s[2]
if s1 < 0:
s1 = - s1
c1 = gmpy2.invert(c1, n)
elif s2 < 0:
s2 = - s2
c2 = gmpy2.invert(c2, n)
if gmpy2.gcd(e1, e2) == 1:
print("e1,e2互质")
message = pow(c1, s1, n) * pow(c2, s2, n) % n
flag = long_to_bytes(message)
print(flag)
elif gmpy2.gcd(e1, e2) != 1:
message = pow(c1, s1, n) * pow(c2, s2, n) % n
common_e = gmpy2.gcd(e1, e2)
print("e1,e2不互质,且公约数为" + str(common_e))
flag = long_to_bytes((gmpy2.iroot(message, common_e)[0]))
print(flag)
if __name__ == '__main__':
deocode()
解密得到随机字符串:dpb3o4zvh47f8xksol7zgvbuullc96,之后选择1进入到guess()方法输入字符串即可得到flag 
ez_signin
题目:
from Crypto.Util.number import *
from secret import flag
p = getPrime(512)
q = getPrime(512)
assert p > q
n = p*q
e = 65536
m = bytes_to_long(flag)
num1 = (pow(p,e,n)-pow(q,e,n)) % n
num2 = pow(p-q,e,n)
c = pow(m,e,n)
print("num1=",num1)
print("num2=",num2)
print("n=",n)
print("c=",c)
n u m 1 ≡ p e − q e m o d n num1 \equiv p^e-q^e \space mod \space n num1≡pe−qe mod n
n u m 2 ≡ ( p − q ) e m o d n , 二项式展开,关于 p q 的式子可消除,那么 n u m 2 ≡ p e + q e m o d n num2 \equiv (p-q)^e \space mod \space n,二项式展开,关于pq的式子可消除,那么num2 \equiv p^e+q^e \space mod \space n num2≡(p−q)e mod n,二项式展开,关于pq的式子可消除,那么num2≡pe+qe mod n
两式相加得到
n u m 1 + n u m 2 ≡ 2 ∗ p e m o d n num1+num2 \equiv 2*p^e \space mod \space n num1+num2≡2∗pe mod n
此时上式与n存在最大公约数p,可得
p = g c d ( n u m 1 + n u m 2 , n ) , q = n / / p p = gcd(num1+num2,n),q = n//p p=gcd(num1+num2,n),q=n//p
此时 e = 65536 = 2 16 e = 65536=2^{16} e=65536=216,且经计算p和q都属于4k+3型素数,直接16次Rabin算法解密即可
解题代码:
from Crypto.Util.number import *
import gmpy2
num1= 134186458247304184975418956047750205959249518467116558944535042073046353646812210914711656218265319503240074967140027248278994209294869476247136854741631971975560846483033205230015783696055443897579440474585892990793595602095853960468928457703619205343030230201261058516219352855127626321847429189498666288452
num2= 142252615203395148320392930915384149783801592719030740337592034613073131106036364733480644482188684184951026866672011061092572389846929838149296357261088256882232316029199097203257003822750826537629358422813658558008420810100860520289261141533787464661186681371090873356089237613080052677646446751824502044253
n= 154128165952806886790805410291540694477027958542517309121222164274741570806324940112942356615458298064007096476638232940977238598879453357856259085001745763666030177657087772721079761302637352680091939676709372354103177660093164629417313468356185431895723026835950366030712541994019375251534778666996491342313
c= 9061020000447780498751583220055526057707259079063266050917693522289697419950637286020502996753375864826169562714946009146452528404466989211057548905704856329650955828939737304126685040898740775635547039660982064419976700425595503919207903099686497044429265908046033565745195837408532764433870408185128447965
p = GCD(num1+num2,n)
q = n//p
x0=gmpy2.invert(p,q)
x1=gmpy2.invert(q,p)
cs = [c]
for i in range(16):
ps = []
for c2 in cs:
r = pow(c2, (p + 1) // 4, p)
s = pow(c2, (q + 1) // 4, q)
x = (r * x1 * q + s * x0 * p) % n
y = (r * x1 * q - s * x0 * p) % n
if x not in ps:
ps.append(x)
if n - x not in ps:
ps.append(n - x)
if y not in ps:
ps.append(y)
if n - y not in ps:
ps.append(n - y)
cs = ps
for m in ps:
flag = long_to_bytes(m)
if b"nssctf" in flag:
print(flag)
break
ez_fac
题目:
from Crypto.Util.number import *
import random
from secret import flag,a0,a1,b0,b1
p = getPrime(512)
q = getPrime(512)
e = getPrime(128)
n = p*q
assert pow(a0,2) + e * pow(b0,2) == n
assert pow(a1,2) + e * pow(b1,2) == n
m = bytes_to_long(flag)
c = pow(m,e,n)
print("c=",c)
print("n=",n)
print("a0=",a0)
print("a1=",a1)
print("b0=",b0)
print("b1=",b1)
论文:《A Note on Euler’s Factoring Problem-Brillhart_Euler_factoring_2009》
当
N = m a 2 + n b 2 N=ma^2+nb^2 N=ma2+nb2
N = m c 2 + n d 2 N = mc^2+nd^2 N=mc2+nd2
则有, N = ( N , a d − b c ) ⋅ N ( N , a d − b c ) N = (N,ad-bc) \cdot \frac{N}{(N,ad-bc)} N=(N,ad−bc)⋅(N,ad−bc)N
那么 , p = g c d ( N , a d − b c ) 那么,p = gcd(N,ad-bc) 那么,p=gcd(N,ad−bc)
解题代码:
import gmpy2
from Crypto.Util.number import *
c= 34007465638566836660852768374211870538357285529060206826620688555044780516477877596651414637089490522614456532732711803500304737160162560168303462221485961593760966240770414498297915175227814336224871400766371471776600674705757656616409870237891336752248110367865552469248343708419900511716030176178698949179
n= 70043427687738872803871163276488213173780425282753969243938124727004843810522473265066937344440899712569316720945145873584064860810161865485251816597432836666987134938760506657782143983431621481190009008491725207321741725979791393566155990005404328775785526238494554357279069151540867533082875900530405903003
a0= 8369195163678456889416121467476480674288621867182572824570660596055739410903686466334448920102666056798356927389728982948229326705483052970212882852055482
a1= 8369195163678456889416121462308686152524805984209312455308229689034789710117101859597220211456125364647704791637845189120538925088375209397006380815921158
b0= 25500181489306553053743739056022091355379036380919737553326529889338409847082228856006303427136881468093863020843230477979
b1= 31448594528370020763962343185054872105044827103889010592635556324009793301024988530934510929565983517651356856506719032859
e = (n-pow(a0,2))//pow(b0,2)
p = gmpy2.gcd(a0*b1-a1*b0,n)
q = n//p
phi = (p-1)*(q-1)
d = gmpy2.invert(e,phi)
m = pow(c,d,n)
flag = long_to_bytes(m)
print(flag)
【大概骄傲就i是高高的城头,喜欢之人,就走在城头之上,脚下是骄傲。】