归并排序的递归实现

归并排序是一种比较排序，通过分治法思想来进行实现的，其基本思想是：

将已有序的子序列合并，得到完全有序的序列，即先使每个子序列有序，再使子序列段间有序。

若将两个有序表合并成一个有序表，称为二路归并。

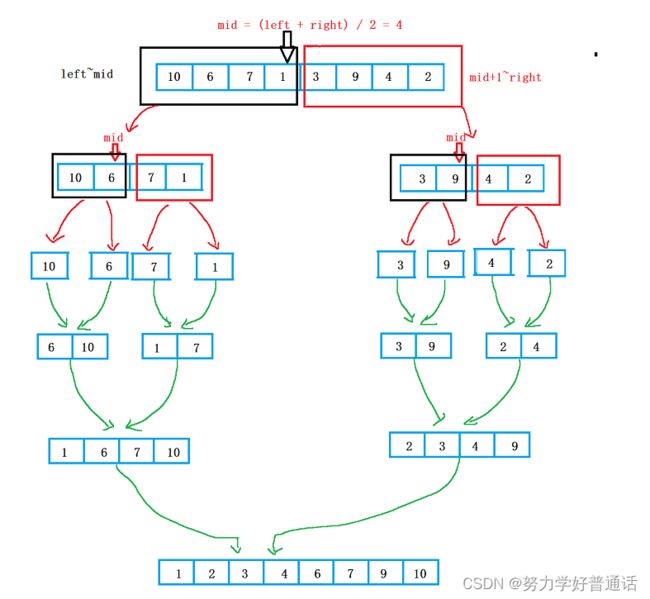
其思想如图所示：

 

这就是归并排序的基本思想，有没有发现和快排的很相似，但大家千万不要搞混，只需要记住一

点，就是快排每进行一次单趟会吧一个元素放到最终位置上，而归并排序不行 ，记住这一点就不

会记混了。

那么如何用递归的思想来实现归并算法呢？

上图中的mid是关键，是链接递归的关键，每得到一个数组就先求mid，之后再进行递归，这样就

可以分为[ left , mid ]和[ mid+1 , right ]这连个区间，从而形成递归，那么递归的结束条件是什么

呢？和快速排序一样，条件是left >= right。

具体交换过程：

相当于两个数组合并的过程，所以需要开辟一个和原数组相同大小的数组，用来存储合并过程中形

成的数组。

交换的代码如下：

int i = left;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] >= a[begin2])
		{
			tmp[i++] = a[begin2++];
		}
		else
		{
			tmp[i++] = a[begin1++];
		}
	}
	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[i++] = a[begin2++];
	}

先将小的元素放入动态开辟的数组中，然后看有没有余下的元素，直接放入动态开辟数组中。

代码如下：

//归并排序
void _MergeSort(int* a, int left, int right, int* tmp)
{
	if (left >= right)
	{
		return;
	}
	int mid = (right + left) / 2;
	int begin1 = left;
	int begin2 = mid + 1;
	int end1 = mid;
	int end2 = right;
	//递归
	_MergeSort(a, begin1, end1, tmp);
	_MergeSort(a, begin2, end2, tmp);
	//合并
	int i = left;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] >= a[begin2])
		{
			tmp[i++] = a[begin2++];
		}
		else
		{
			tmp[i++] = a[begin1++];
		}
	}
	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[i++] = a[begin2++];
	}

	memcpy(a + left, tmp + left, sizeof(int) * (right - left + 1));
}

//归并排序
void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		return;
	}
	_MergeSort(a, 0, n - 1, tmp);
	free(tmp);
}

一定要将最后的结果拷贝回原数组中。 

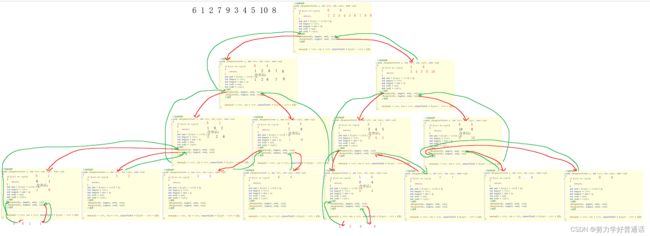
接下来我们画一下它的递归展开图，方便理解：

 

如图所示，其中红色箭头与图一的红色箭头对应，绿色箭头与图一的绿色箭头对应，相信大家看完

这两幅图后能明白递归的真实情况，这就是递归归并排序。