机器学习:使用matlab实现逻辑回归解决数字识别(多元分类)问题
文章目录
- 前置章节
- 数据载入
- 数据可视化
- 代价-梯度函数
- 一对多完成多元分类
- 预测
前置章节
二元分类问题的逻辑回归包含原理及实现。
这次做多元分类,目的是能够识别 20 × 20 20\times20 20×20像素的手写体数字。
数据载入
来自MINST的手写数字数据库,矩阵X中是5000张图片的灰度构成的数据集,因为图片像素是20×20,所以矩阵每行有400个元素,为图片的灰度。y向量表明图片中的数字是什么,因为matlab数组下标从1开始,所以我们把数字0对应的数据映射到10上。
% Load saved matrices from file
load('ex3data1.mat');
% The matrices X and y will now be in your MATLAB environment
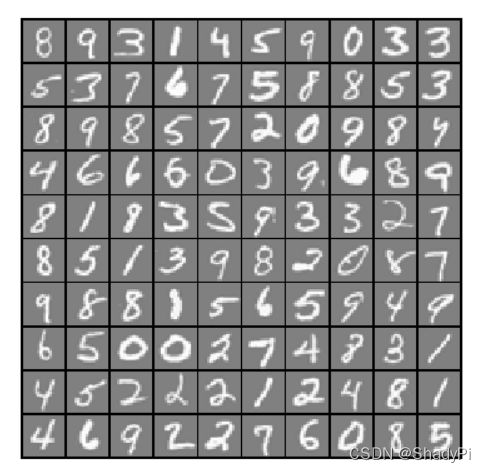
数据可视化
随机抽出几张图片瞅一瞅,吴恩达的代码没仔细研究,先放在这里:
function [h, display_array] = displayData(X, example_width)
%DISPLAYDATA Display 2D data in a nice grid
% [h, display_array] = DISPLAYDATA(X, example_width) displays 2D data
% stored in X in a nice grid. It returns the figure handle h and the
% displayed array if requested.
% Set example_width automatically if not passed in
if ~exist('example_width', 'var') || isempty(example_width)
example_width = round(sqrt(size(X, 2)));
end
% Gray Image
colormap(gray);
% Compute rows, cols
[m n] = size(X);
example_height = (n / example_width);
% Compute number of items to display
display_rows = floor(sqrt(m));
display_cols = ceil(m / display_rows);
% Between images padding
pad = 1;
% Setup blank display
display_array = - ones(pad + display_rows * (example_height + pad), ...
pad + display_cols * (example_width + pad));
% Copy each example into a patch on the display array
curr_ex = 1;
for j = 1:display_rows
for i = 1:display_cols
if curr_ex > m,
break;
end
% Copy the patch
% Get the max value of the patch
max_val = max(abs(X(curr_ex, :)));
display_array(pad + (j - 1) * (example_height + pad) + (1:example_height), ...
pad + (i - 1) * (example_width + pad) + (1:example_width)) = ...
reshape(X(curr_ex, :), example_height, example_width) / max_val;
curr_ex = curr_ex + 1;
end
if curr_ex > m,
break;
end
end
% Display Image
h = imagesc(display_array, [-1 1]);
% Do not show axis
axis image off
drawnow;
end
m = size(X, 1);
% Randomly select 100 data points to display
rand_indices = randperm(m);
sel = X(rand_indices(1:100), :);
displayData(sel);
代价-梯度函数
ex3的意思是在ex2的基础上让代价-梯度函数向量化,即通过矩阵运算省略for循环,不过我已经在ex2搞定了,有关公式与推导请看链接,这里不再赘述。
function [J, grad] = lrCostFunction(theta, X, y, lambda)
%LRCOSTFUNCTION Compute cost and gradient for logistic regression with
%regularization
% J = LRCOSTFUNCTION(theta, X, y, lambda) computes the cost of using
% theta as the parameter for regularized logistic regression and the
% gradient of the cost w.r.t. to the parameters.
% Initialize some useful values
m = length(y); % number of training examples
% You need to return the following variables correctly
J = 0;
grad = zeros(size(theta));
% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta.
% You should set J to the cost.
% Compute the partial derivatives and set grad to the partial
% derivatives of the cost w.r.t. each parameter in theta
%
% Hint: The computation of the cost function and gradients can be
% efficiently vectorized. For example, consider the computation
%
% sigmoid(X * theta)
%
% Each row of the resulting matrix will contain the value of the
% prediction for that example. You can make use of this to vectorize
% the cost function and gradient computations.
%
% Hint: When computing the gradient of the regularized cost function,
% there're many possible vectorized solutions, but one solution
% looks like:
% grad = (unregularized gradient for logistic regression)
% temp = theta;
% temp(1) = 0; % because we don't add anything for j = 0
% grad = grad + YOUR_CODE_HERE (using the temp variable)
%
h=sigmoid(X*theta);
J=y'*log(h)+(1.-y')*log(1.-h);
J=-J/m;
J=J+(lambda/(2*m)).*(theta'*theta-theta(1)^2);
grad=X'*(h-y);
grad=grad./m;
tmp=grad(1);
grad=grad+(lambda/m).*theta;
grad(1)=tmp;
% =============================================================
grad = grad(:);
end
一对多完成多元分类
一对多的思想在这个博客里,大意就是把多元分类转化为二元分类,因此我们需要训练多个(在数字识别问题里为10个)分类器,就有10个参数向量,构成一个参数矩阵。
训练一个分类器的过程跟二元分类时一样,不过在二元分类中我们用的是matlab自带的函数fminunc,而这里我们用的是吴恩达提供的函数fmincg,两者优化的结果差不多,但fmincg在处理参数数量较多的优化时效率更高。
fmincg函数,为了让博客不要太过冗长,我删除了一些注释:
function [X, fX, i] = fmincg(f, X, options, P1, P2, P3, P4, P5)
% Usage: [X, fX, i] = fmincg(f, X, options, P1, P2, P3, P4, P5)
% Read options
if exist('options', 'var') && ~isempty(options) && isfield(options, 'MaxIter')
length = options.MaxIter;
else
length = 100;
end
RHO = 0.01; % a bunch of constants for line searches
SIG = 0.5; % RHO and SIG are the constants in the Wolfe-Powell conditions
INT = 0.1; % don't reevaluate within 0.1 of the limit of the current bracket
EXT = 3.0; % extrapolate maximum 3 times the current bracket
MAX = 20; % max 20 function evaluations per line search
RATIO = 100; % maximum allowed slope ratio
argstr = ['feval(f, X']; % compose string used to call function
for i = 1:(nargin - 3)
argstr = [argstr, ',P', int2str(i)];
end
argstr = [argstr, ')'];
if max(size(length)) == 2, red=length(2); length=length(1); else red=1; end
S=['Iteration '];
i = 0; % zero the run length counter
ls_failed = 0; % no previous line search has failed
fX = [];
[f1 df1] = eval(argstr); % get function value and gradient
i = i + (length<0); % count epochs?!
s = -df1; % search direction is steepest
d1 = -s'*s; % this is the slope
z1 = red/(1-d1); % initial step is red/(|s|+1)
while i < abs(length) % while not finished
i = i + (length>0); % count iterations?!
X0 = X; f0 = f1; df0 = df1; % make a copy of current values
X = X + z1*s; % begin line search
[f2 df2] = eval(argstr);
i = i + (length<0); % count epochs?!
d2 = df2'*s;
f3 = f1; d3 = d1; z3 = -z1; % initialize point 3 equal to point 1
if length>0, M = MAX; else M = min(MAX, -length-i); end
success = 0; limit = -1; % initialize quanteties
while 1
while ((f2 > f1+z1*RHO*d1) || (d2 > -SIG*d1)) && (M > 0)
limit = z1; % tighten the bracket
if f2 > f1
z2 = z3 - (0.5*d3*z3*z3)/(d3*z3+f2-f3); % quadratic fit
else
A = 6*(f2-f3)/z3+3*(d2+d3); % cubic fit
B = 3*(f3-f2)-z3*(d3+2*d2);
z2 = (sqrt(B*B-A*d2*z3*z3)-B)/A; % numerical error possible - ok!
end
if isnan(z2) || isinf(z2)
z2 = z3/2; % if we had a numerical problem then bisect
end
z2 = max(min(z2, INT*z3),(1-INT)*z3); % don't accept too close to limits
z1 = z1 + z2; % update the step
X = X + z2*s;
[f2 df2] = eval(argstr);
M = M - 1; i = i + (length<0); % count epochs?!
d2 = df2'*s;
z3 = z3-z2; % z3 is now relative to the location of z2
end
if f2 > f1+z1*RHO*d1 || d2 > -SIG*d1
break; % this is a failure
elseif d2 > SIG*d1
success = 1; break; % success
elseif M == 0
break; % failure
end
A = 6*(f2-f3)/z3+3*(d2+d3); % make cubic extrapolation
B = 3*(f3-f2)-z3*(d3+2*d2);
z2 = -d2*z3*z3/(B+sqrt(B*B-A*d2*z3*z3)); % num. error possible - ok!
if ~isreal(z2) || isnan(z2) || isinf(z2) || z2 < 0 % num prob or wrong sign?
if limit < -0.5 % if we have no upper limit
z2 = z1 * (EXT-1); % the extrapolate the maximum amount
else
z2 = (limit-z1)/2; % otherwise bisect
end
elseif (limit > -0.5) && (z2+z1 > limit) % extraplation beyond max?
z2 = (limit-z1)/2; % bisect
elseif (limit < -0.5) && (z2+z1 > z1*EXT) % extrapolation beyond limit
z2 = z1*(EXT-1.0); % set to extrapolation limit
elseif z2 < -z3*INT
z2 = -z3*INT;
elseif (limit > -0.5) && (z2 < (limit-z1)*(1.0-INT)) % too close to limit?
z2 = (limit-z1)*(1.0-INT);
end
f3 = f2; d3 = d2; z3 = -z2; % set point 3 equal to point 2
z1 = z1 + z2; X = X + z2*s; % update current estimates
[f2 df2] = eval(argstr);
M = M - 1; i = i + (length<0); % count epochs?!
d2 = df2'*s;
end % end of line search
if success % if line search succeeded
f1 = f2; fX = [fX' f1]';
fprintf('%s %4i | Cost: %4.6e\r', S, i, f1);
s = (df2'*df2-df1'*df2)/(df1'*df1)*s - df2; % Polack-Ribiere direction
tmp = df1; df1 = df2; df2 = tmp; % swap derivatives
d2 = df1'*s;
if d2 > 0 % new slope must be negative
s = -df1; % otherwise use steepest direction
d2 = -s'*s;
end
z1 = z1 * min(RATIO, d1/(d2-realmin)); % slope ratio but max RATIO
d1 = d2;
ls_failed = 0; % this line search did not fail
else
X = X0; f1 = f0; df1 = df0; % restore point from before failed line search
if ls_failed || i > abs(length) % line search failed twice in a row
break; % or we ran out of time, so we give up
end
tmp = df1; df1 = df2; df2 = tmp; % swap derivatives
s = -df1; % try steepest
d1 = -s'*s;
z1 = 1/(1-d1);
ls_failed = 1; % this line search failed
end
if exist('OCTAVE_VERSION')
fflush(stdout);
end
end
fprintf('\n');
之后,for循环做10次求解最小值即可得到参数矩阵(一些常量应该在循环外定义更好)注意这里吴恩达定义的参数矩阵是10×(n+1)的,我们求出来的是(n+1)×1的列向量,所以储存的时候要转置一下:
function [all_theta] = oneVsAll(X, y, num_labels, lambda)
%ONEVSALL trains multiple logistic regression classifiers and returns all
%the classifiers in a matrix all_theta, where the i-th row of all_theta
%corresponds to the classifier for label i
% [all_theta] = ONEVSALL(X, y, num_labels, lambda) trains num_labels
% logistic regression classifiers and returns each of these classifiers
% in a matrix all_theta, where the i-th row of all_theta corresponds
% to the classifier for label i
% Some useful variables
m = size(X, 1);
n = size(X, 2);
% You need to return the following variables correctly
all_theta = zeros(num_labels, n + 1);
% Add ones to the X data matrix
X = [ones(m, 1) X];
% ====================== YOUR CODE HERE ======================
% Example Code for fmincg:
%
% % Set Initial theta
% initial_theta = zeros(n + 1, 1);
%
% % Set options for fminunc
% options = optimset('GradObj', 'on', 'MaxIter', 50);
%
% % Run fmincg to obtain the optimal theta
% % This function will return theta and the cost
% [theta] = ...
% fmincg (@(t)(lrCostFunction(t, X, (y == c), lambda)), ...
% initial_theta, options);
%
for i=1:num_labels
initial_theta=zeros(n+1,1);
options = optimset('GradObj', 'on', 'MaxIter', 50);
[theta]=fmincg(@(t)lrCostFunction(t,X,(y==i),lambda),initial_theta,options);
all_theta(i,:)=theta';
end
% =========================================================================
end
num_labels = 10; % 10 labels, from 1 to 10
lambda = 0.1;
[all_theta] = oneVsAll(X, y, num_labels, lambda);
运行完上方的代码,我们就得到了参数矩阵。
预测
接下来就可以利用我们求出的参数来进行预测了,通过
h θ ( X ) = g ( X Θ T ) h_\theta(X)=g(X\Theta^T) hθ(X)=g(XΘT)
算出图像为某个数字的概率,再利用[~,p]=max(A,[],2)将矩阵每行最大值的下标取出来,就可以知道该图像最可能是哪个数字。
function p = predictOneVsAll(all_theta, X)
%PREDICT Predict the label for a trained one-vs-all classifier. The labels
%are in the range 1..K, where K = size(all_theta, 1).
% p = PREDICTONEVSALL(all_theta, X) will return a vector of predictions
% for each example in the matrix X. Note that X contains the examples in
% rows. all_theta is a matrix where the i-th row is a trained logistic
% regression theta vector for the i-th class. You should set p to a vector
% of values from 1..K (e.g., p = [1; 3; 1; 2] predicts classes 1, 3, 1, 2
% for 4 examples)
m = size(X, 1);
num_labels = size(all_theta, 1);
% You need to return the following variables correctly
p = zeros(size(X, 1), 1);
% Add ones to the X data matrix
X = [ones(m, 1) X];
% ====================== YOUR CODE HERE ======================
% Instructions: Complete the following code to make predictions using
% your learned logistic regression parameters (one-vs-all).
% You should set p to a vector of predictions (from 1 to
% num_labels).
%
% Hint: This code can be done all vectorized using the max function.
% In particular, the max function can also return the index of the
% max element, for more information see 'help max'. If your examples
% are in rows, then, you can use max(A, [], 2) to obtain the max
% for each row.
%
[~,p]=max(sigmoid(X*all_theta'),[],2);
% =========================================================================
end
最后得到本逻辑回归算法在训练集上的准确率为94.9%。
pred = predictOneVsAll(all_theta, X);
fprintf('\nTraining Set Accuracy: %f\n', mean(double(pred == y)) * 100);