支持向量机(SVM)
支持向量机 support vector machines
- 1.线性可支持向量机与硬间隔最大化
-
- 1.1 线性可分支持向量机
- 1.2 函数间隔和几何间隔
- 1.3 间隔最大化
- 1.4 学习的对偶算法
- 2.线性支持向量机与软间隔最大化
- 3.非线性支持向量机与核函数
-
- 3.1 核技巧
- 3.2 正定核
- 3.3 常用核函数
- 4.SMO序列最小最优化算法原理
SVM 是一个非常美丽的算法,具有完善的数学理论,曾经把神经网络按在地上摩擦,所以决定花点时间去学习以及整理一下。
支持向量机是一种二类分类模型。其基本模型是定义在特征空间上的间隔最大的线性分类器,间隔最大使它有别于感知机;支持向量机还包括核技巧,这使它成为实质上的非线性分类器。支持向量机的学习策略就是间隔最大化,可形式化为一个求解凸二次规划的问题,也等价于正则化的合页损失函数的最小化问题。支持向量机的学习算法是求解凸二次规划的最优化算法。
支持向量机学习方法包含构建由简至繁的模型:
- 线性可支持向量机:当训练数据线性可分时,通过硬间隔最大化(hard margin maximization),学习一个线性的分类器,即线性可分支持向量机,又称为硬间隔支持向量机;
- 线性支持向量机:当训练数据近似线性可分时,通过软间隔最大化(soft margin maximization),也学习一个线性的分类器,即线性支持向量机,又称为软间隔支持向量机;
- 非线性支持向量机:当训练数据线性不可分时,通过使用核技巧(kernel trick)及软间隔最大化,学习非线性支持向量机。
1.线性可支持向量机与硬间隔最大化
1.1 线性可分支持向量机
首先的学习的目标是在特征空间中找到一个分离超平面,能将实例分到不同的类。分离超平面对应于方程 w ⋅ x + b = 0 w\cdot x +b=0 w⋅x+b=0,它由法向量 w w w和截距 b b b决定,可用 ( w , b ) (w,b) (w,b)来表示。分离超平面将特征空间划分为两部分,一部分是正类,一部分是负类。法向量指向的一侧为正类,另一侧为负类。

线性可支持向量机
给定线性可分训练数据集,通过间隔最大化或等价地求解相应的凸二次规划问题学习得到的分离超平面为:
w ∗ ⋅ x + b ∗ = 0 w^*\cdot x+b^*=0 w∗⋅x+b∗=0
以及相应的分类决策函数:
f ( x ) = s i g n ( w ∗ ⋅ x + b ∗ ) f(x) = sign(w^*\cdot x+b^*) f(x)=sign(w∗⋅x+b∗)

1.2 函数间隔和几何间隔
在超平面 w ′ x + b = 0 w'x+b=0 w′x+b=0确定的情况下, ∣ w ′ x + b ∣ |w'x+b| ∣w′x+b∣能够代表点 x x x距离超平面的远近,易知:当 w ′ x + b > 0 w'x+b>0 w′x+b>0时,表示x在超平面的一侧(正类,类标为1),而当 w ′ x + b < 0 w'x+b<0 w′x+b<0时,则表示 x x x在超平面的另外一侧(负类,类别为-1),因此 ( w ′ x + b ) y (w'x+b)y (w′x+b)y的正负性恰能表示数据点x是否被分类正确。于是便引出了*函数间隔**的定义(functional margin):
函数间隔:
对于给定的训练集 T T T和超平面 ( w , b ) (w,b) (w,b),定义超平面 ( w , b ) (w,b) (w,b)关于样本 ( x i , y i ) (x_i,y_i) (xi,yi)的函数间隔为
γ ^ i = y i ( w ⋅ x i + b ) \hat{\gamma}_i=y_i(w\cdot x_i +b) γ^i=yi(w⋅xi+b)
定义超平面 ( w , b ) (w,b) (w,b)关于训练集 T T T的函数间隔为超平面 ( w , b ) (w,b) (w,b)关于 T T T中所有样本点 ( x i , y i ) (x_i,y_i) (xi,yi)的函数间隔之最小值,即
γ ^ = m i n i = 1 , ⋯ , N γ ^ i \hat{\gamma} = min_{i=1,\cdots,N} \hat{\gamma}_i γ^=mini=1,⋯,Nγ^i
可以看出:这样定义的函数间隔在处理SVM上会有问题,当超平面的两个参数w和b同比例改变时,函数间隔也会跟着改变,但是实际上超平面还是原来的超平面,并没有变化。例如: w 1 x 1 + w 2 x 2 + w 3 x 3 + b = 0 w_1x_1+w_2x_2+w_3x_3+b=0 w1x1+w2x2+w3x3+b=0其实等价于 2 w 1 x 1 + 2 w 2 x 2 + 2 w 3 x 3 + 2 b = 0 2w_1x_1+2w_2x_2+2w_3x_3+2b=0 2w1x1+2w2x2+2w3x3+2b=0,但计算的函数间隔却翻了一倍。从而引出了能真正度量点到超平面距离的概念–几何间隔(geometrical margin)。
几何间隔:
代表的则是数据点到超平面的真实距离,对于超平面 w ′ x + b = 0 w'x+b=0 w′x+b=0, w w w代表的是该超平面的法向量,设 x ∗ x^* x∗为超平面外一点x在法向量 w w w方向上的投影点, x x x与超平面的距离为 r r r,则有 x ∗ = x − r ( w / ∣ ∣ w ∣ ∣ ) x^*=x-r(w/||w||) x∗=x−r(w/∣∣w∣∣),又 x ∗ x^* x∗在超平面上,即 w ′ x ∗ + b = 0 w'x*+b=0 w′x∗+b=0,代入即可得:
γ i = y i ( w ∣ ∣ w ∣ ∣ ⋅ x i + b ∣ ∣ w ∣ ∣ ) \gamma_i=y_i({w \over ||w||}\cdot x_i +{b \over ||w||}) γi=yi(∣∣w∣∣w⋅xi+∣∣w∣∣b)
超平面 ( w , b ) (w,b) (w,b)关于样本点 ( x i , y i ) (x_i,y_i) (xi,yi)的几何间隔一般是实例点到超平面的带符号的距离。
上述函数间隔与几何间隔的定义可以看出:实质上函数间隔就是 ∣ w ′ x + b ∣ |w'x+b| ∣w′x+b∣,而几何间隔就是点到超平面的距离。
函数间隔与几何间隔有下面关系:
γ i = γ i ^ ∣ ∣ w ∣ ∣ \gamma_i = {\hat{\gamma_i} \over ||w||} γi=∣∣w∣∣γi^
γ = γ ^ ∣ ∣ w ∣ ∣ \gamma = {\hat{\gamma} \over ||w||} γ=∣∣w∣∣γ^
如果 ∣ ∣ w ∣ ∣ = 1 ||w||=1 ∣∣w∣∣=1,那么函数间隔和几何间隔相等。如果超平面参数 w w w和 b b b成比例改变(超平面没有改变),函数间隔也按此比例改变,而几何间隔不变。
1.3 间隔最大化
通过前面的分析可知:函数间隔不适合用来最大化间隔,因此这里我们要找的最大间隔指的是几何间隔,于是最大间隔分类器的目标函数定义为:

一般地,我们令 r ^ \hat{r} r^为1(这样做的目的是为了方便推导和目标函数的优化),从而上述目标函数转化为:

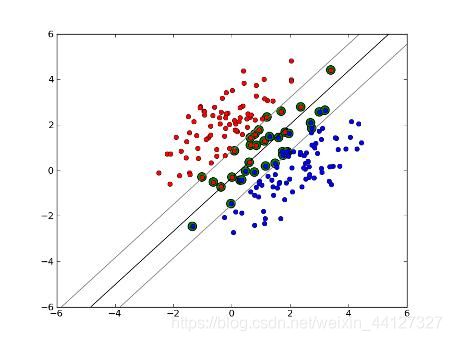
对于 y ( w ′ x + b ) = 1 y(w'x+b)=1 y(w′x+b)=1的数据点,即下图中位于 w ′ x + b = 1 w'x+b=1 w′x+b=1或 w ′ x + b = − 1 w'x+b=-1 w′x+b=−1上的数据点,我们称之为支持向量(support vector),易知:对于所有的支持向量,它们恰好满足 y ( w ′ x + b ) = 1 y(w'x+b)=1 y(w′x+b)=1,而所有不是支持向量的点,有 y ( w ′ x + b ) > 1 y(w'x+b)>1 y(w′x+b)>1。

1.4 学习的对偶算法
2.线性支持向量机与软间隔最大化
3.非线性支持向量机与核函数
3.1 核技巧
3.2 正定核
3.3 常用核函数
4.SMO序列最小最优化算法原理
SMO 是微软研究院的 John C. Platt 在《Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines》一文中提出的,其基本思想是:把含有 m 个参数的原始问题分解成多个子问题分别求解,每个子问题只需要求解两个参数,这样SMO算法就将一个复杂的优化问题转化为一个比较简单的两变量优化问题。每次启发式选择两个变量进行优化,不断循环,直到达到函数最优值。
- 参考:统计学习方法 (第二版) 李航老师
西瓜书