线性判别分析(Linear Discriminant Analysis,LDA)
一、LDA的基本思想
线性判别式分析(Linear Discriminant Analysis, LDA),也叫做Fisher线性判别(Fisher Linear Discriminant ,FLD),是模式识别的经典算法,它是在1996年由Belhumeur引入模式识别和人工智能领域的。线性鉴别分析的基本思想是将高维的模式样本投影到最佳鉴别矢量空间,以达到抽取分类信息和压缩特征空间维数的效果,投影后保证模式样本在新的子空间有最大的类间距离和最小的类内距离,即模式在该空间中有最佳的可分离性。
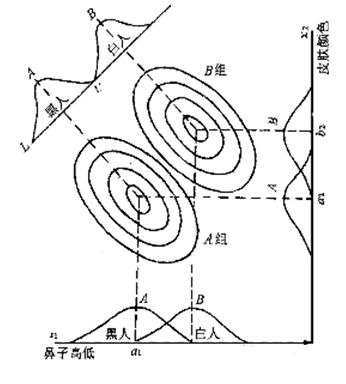
如下图所示,根据肤色和鼻子高低将人分为白人和黑人,样本中白人的鼻子高低和皮肤颜色主要集中A组区域,黑人的鼻子高低和皮肤颜色主要集中在B组区域,很显然A组合B组在空间上明显分离的,将A组和B组上的点都投影到直线L上,分别落在直线L的不同区域,这样就线性的将黑人和白人分开了。一旦有未知样本需要区分,只需将皮肤颜色和鼻子高低代入直线L的方程,即可判断出未知样本的所属的分类。
因此,LDA的关键步骤是选择合适的投影方向,即建立合适的线性判别函数(非线性不是本文的重点)。
二、LDA的计算过程
1、代数表示的计算过程
设已知两个总体A和B,在A、B两总体分别提出m个特征 ,然后从A、B两总体中分别抽取出
,然后从A、B两总体中分别抽取出 、
、 个样本,得到A、B两总体的样本数据如下:
个样本,得到A、B两总体的样本数据如下:
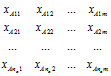 和
和 
假设存在这样的线性函数(投影平面),可以将A、B两类样本投影到该平面上,使得A、B两样本在该直线上的投影满足以下两点:(1)两类样本的中心距离最远;(2)同一样本内的所有投影距离最近。我们将该线性函数表达如下:
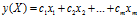
将A总体的第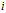 个样本点
个样本点
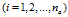 投影到
投影到 平面上得到投影点
平面上得到投影点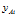 ,即
,即
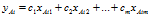

A总体的样本在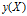 平面投影的重心为
平面投影的重心为

其中 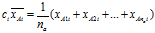
同理可以得到B在 平面上的投影点
平面上的投影点
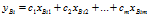
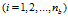
以及B总体样本在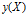 平面投影的重心为
平面投影的重心为

其中
按照Fisher的思想,不同总体A、B的投影点应尽量分开,用数学表达式表示为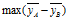 ,而同一总体的投影点的距离应尽可能的小,用数学表达式表示为
,而同一总体的投影点的距离应尽可能的小,用数学表达式表示为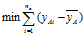 ,
,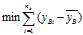 ,合并得到
,合并得到
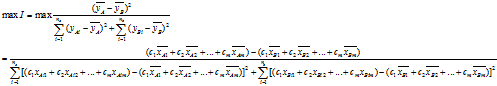
求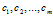 从而使得
从而使得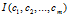 得到最大值,分别对
得到最大值,分别对 进行求导即可,详细步骤不表。
进行求导即可,详细步骤不表。
2、向量表示的计算过程
上述LDA判别的代数表述方法直观,单较为复杂,而且两个以上的样本总体不适用,向量和矩阵包含更丰富的信息,表达能力更强,本小结将介绍LDA的向量表示的计算过程。
假设对于一个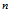 维空间有
维空间有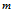 个样本分别为
个样本分别为 即 每个样本
即 每个样本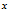 是一个
是一个 行的矩阵,其中
行的矩阵,其中 表示属于
表示属于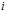 类的样本个数,假设有一个有c个类,则
类的样本个数,假设有一个有c个类,则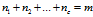 。
。
约定数学符号和表达式如下:
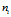 -- 第
-- 第 类的样本个数;
类的样本个数; --第
--第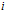 个样本;
个样本;
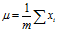 --所有样本的均值;
--所有样本的均值;
 --类
--类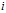 的样本均值;
的样本均值;
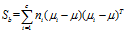 -- 类间离散度矩阵,协方差矩阵;
-- 类间离散度矩阵,协方差矩阵;
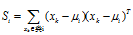 -- 第
-- 第 类内离散度矩阵;
类内离散度矩阵;
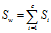 -- 所有类的类内离散程度总和;
-- 所有类的类内离散程度总和;
 -- 第
-- 第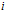 类的样本个数;
类的样本个数;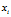 --第
--第 个样本;
个样本;
我们可以知道矩阵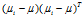 的实际意义是一个协方差矩阵,这个矩阵所刻画的是该类与样本总体之间的关系,其中该矩阵对角线上的函数所代表的是该类相对样本总体的方差(即分散度),而非对角线上的元素所代表是该类样本总体均值的协方差(即该类和总体样本的相关联度或称冗余度),所以
的实际意义是一个协方差矩阵,这个矩阵所刻画的是该类与样本总体之间的关系,其中该矩阵对角线上的函数所代表的是该类相对样本总体的方差(即分散度),而非对角线上的元素所代表是该类样本总体均值的协方差(即该类和总体样本的相关联度或称冗余度),所以 把所有样本中各个样本根据自己所属的类计算出样本与总体的协方差矩阵的总和,这从宏观上描述了所有类和总体之间的离散冗余程度。同理,
把所有样本中各个样本根据自己所属的类计算出样本与总体的协方差矩阵的总和,这从宏观上描述了所有类和总体之间的离散冗余程度。同理, 为分类内各个样本和所属类之间的协方差矩阵之和,它所刻画的是从总体来看类内各个样本与类之间(这里所刻画的类特性是由是类内各个样本的平均值矩阵构成)离散度,其实从中可以看出不管是类内的样本期望矩阵还是总体样本期望矩阵,它们都只是充当一个媒介作用,不管是类内还是类间离散度矩阵都是从宏观上刻画出类与类之间的样本的离散度和类内样本和样本之间的离散度。
为分类内各个样本和所属类之间的协方差矩阵之和,它所刻画的是从总体来看类内各个样本与类之间(这里所刻画的类特性是由是类内各个样本的平均值矩阵构成)离散度,其实从中可以看出不管是类内的样本期望矩阵还是总体样本期望矩阵,它们都只是充当一个媒介作用,不管是类内还是类间离散度矩阵都是从宏观上刻画出类与类之间的样本的离散度和类内样本和样本之间的离散度。
LDA做为一个分类的算法,我们当然希望它所分的类之间耦合度低,类内的聚合度高,即类内离散度矩阵的中的数值要小,而类间离散度矩阵中的数值要大,这样的分类的效果才好。这里我们引入Fisher鉴别准则表达式:
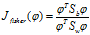
其中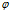 为任一
为任一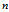 维列矢量。Fisher线性鉴别分析就是选取使得
维列矢量。Fisher线性鉴别分析就是选取使得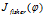 达到最大值的矢量
达到最大值的矢量 作为投影方向,其物理意义就是投影后的样本具有最大的类间离散度和最小的类内离散度。我们把公式
作为投影方向,其物理意义就是投影后的样本具有最大的类间离散度和最小的类内离散度。我们把公式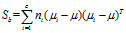 和公式
和公式 代入公式
代入公式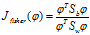 得到:
得到:

重点来了(给它加100个粗,哈哈),设矩阵 ,其中
,其中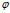 可以看成是一个空间(相当于代数表达式里的
可以看成是一个空间(相当于代数表达式里的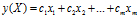 ),也就是说
),也就是说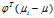 就是矩阵
就是矩阵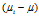 构成的低维空间
构成的低维空间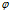 (超平面)的投影,联想一下特征值的表达式
(超平面)的投影,联想一下特征值的表达式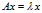 。
。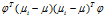 也可表示为
也可表示为 ,而当样本为列向量时,
,而当样本为列向量时,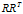 即表示
即表示 在
在 空间的几何距离的平方。所以可以推出fisher线性鉴别分析表达式的分子即为样本在投影
空间的几何距离的平方。所以可以推出fisher线性鉴别分析表达式的分子即为样本在投影 空间下的类间几何距离的平方和,同理也可推出分母为样本在投影
空间下的类间几何距离的平方和,同理也可推出分母为样本在投影 空间下的类内几何距离的平方差,所以分类问题就转化到找一个低维空间使得样本投影到该空间下时,投影下来的类间距离平方和与类内距离平方和之比最大,即最佳分类效果。
空间下的类内几何距离的平方差,所以分类问题就转化到找一个低维空间使得样本投影到该空间下时,投影下来的类间距离平方和与类内距离平方和之比最大,即最佳分类效果。
所以根据上述思想,即通过最优化下面的准则函数找到有一组最优鉴别矢量构成的投影矩阵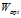 (这里我们也可以看出1/m可以通过分子分母约掉,所以前面所提到的第一组公式和第二组公式所表达的效果是一样的).
(这里我们也可以看出1/m可以通过分子分母约掉,所以前面所提到的第一组公式和第二组公式所表达的效果是一样的).
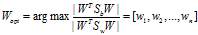
可以证明,当 为非奇异(一般在实现LDA算法时,都会对样本做一次PCA算法的降维,消除样本的冗余度,从而保证
为非奇异(一般在实现LDA算法时,都会对样本做一次PCA算法的降维,消除样本的冗余度,从而保证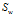 是非奇异阵,当然即使
是非奇异阵,当然即使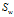 为奇异阵也是可以解的,可以把
为奇异阵也是可以解的,可以把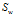 或
或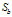 对角化,这里不做讨论,假设都是非奇异的情况)时,最佳投影矩阵
对角化,这里不做讨论,假设都是非奇异的情况)时,最佳投影矩阵 的列向量恰为下来广义特征方程
的列向量恰为下来广义特征方程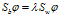 的d个最大的特征值所对应的特征向量(矩阵
的d个最大的特征值所对应的特征向量(矩阵 的特征向量),且最优投影轴的个数d<=c-1。
的特征向量),且最优投影轴的个数d<=c-1。
根据 式可以推出
式可以推出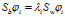
又由于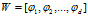
把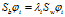 式代入
式代入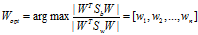 式可得:
式可得:

所以根据公式意义来看,要使max最大则只要取 即可,所可得到如下结论:投影矩阵
即可,所可得到如下结论:投影矩阵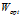 的列向量为d(自取)个最大特征值对应的特征向量,其中
的列向量为d(自取)个最大特征值对应的特征向量,其中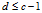
三、LDA的应用实例分析
R语言的MASS包中有实现LDA的函数,函数名为lda,具体的应用实例请参考文章:
http://xccds1977.blogspot.tw/2011/12/r_27.html
------------------------------------
文中的内容大部分来自网络,仅作为本人的学习笔记