从坐标系图中理解“空间变换”

 

for a better view plz follow this link (from evernote).

-----------------------------------------------------

 

长久以来，“空间变换”这个话题对我就像是谜一样的存在。我了解这种事物所讲的起因和结果，却始终对当中的过程参悟不透。我知道，这是因为大学时经常逃课的结果：至今线性代数这门知识，都不曾系统性地学过一遍。今日，当每每不得不接触这个令人胆寒的东西时，我总是小心翼翼地记着那"咒语"般的规则——总之把矩阵和向量那么乘一下，就算是转了么。

 

不过最近，在学习“ 切空间"时，竟偶然意识到，原来可以用在几何学中经常用到的工具“坐标系图”来直观地分析这种变换。所以，我想就这个新的认识再在这里分享一下。

 

让我们从一个实际的例子入手：下图是一个 用两维的笛卡尔坐标系表示的二维空间。

 

 

 

 

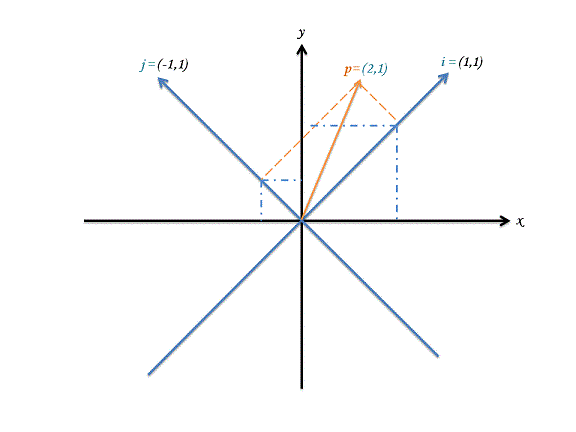
其中，黑色 坐标系  x-y 代表一个二维空间 ； 蓝色坐标系  i-j 代表另外一个二维空间。已知蓝色坐标系轴在黑色坐标系下对应的值是i=(1,1), j=(-1,1)，又知橙色向量 p 处在 i-j 空间中，其坐标值为(2,1)。现在的问题是，这个 p 被转换到黑色坐标系 x-y 空间下它的坐标值是什么？

 

解决这个问题一个最关键也最直接的想法是“向量分解与再合成”。p 可以被分解到  i 和  j 两个方向，得到  p= 2 i+ j；同时  i 又可以分解到  x 和  y 两个方向，得到  i =  x +  y，另外  j 也可以分解得到  j = - x +  y。于是，我们全部展开，就得到  p_(i-j) = 2 i +  j = 2( x +  y) + (- x +  y) =  x + 3 y =  p _{(x-y) 。}因此点  p 在  x-y 空间下的坐标值为 (1,3)。

这种方法可以用来讨论更一般的情况。假设 p点在  i-j 坐标系下为 (k1,k2)，在  x-y 坐标系下为( q1,q2)。同样地有基向量  i 对应在  x-y 空间中为 (m1,m2)； j 对应在  x-y 空间中为 (n1,n2)。于是我们有以下推导，

i = m1 x + m2 y， j = n1 x + n2 y

 

于是，

 

  p_(i-j)  = k1 i + k2 j

         = k1( m1x + m2y) + k2( n1x + n2y)

         = (k1m1 + k2n1) x + (k1m2 + k2n2) y

 

于是，

 

  p_(i-j)  = ( k1m1 + k2n1, k1m2 + k2n2)

         =  (q1, q2)

         =  p _(x-y)

 

得到，

 

q1 = k1m1 + k2n1

q2 = k1m2 + k2n2

 

变换成矩阵形式，

 

 

其中 (k1,k2)是  i-j 空间下的坐标值，而 (q1,q2)是  x-y 空间下的坐标值。中间的矩阵就是用来做转换的矩阵。从中我们可以发现，如果竖着来观察，向量 (m1,m2)就是基向量  i 在  x-y 空间下的坐标值，而向量 (n1,n2)则是基向量  j 在  x-y 空间下的坐标值。这个矩阵，实际上就是由空间  i-j 下的基向量在空间  x-y 下的坐标值构成的。这一点，以前我就知道。但直到今天，我才理解了为什么是这样。

 

因为知道了底细，所以一些长久以来伴随的困惑也随之消解。比如，对于一个变换表达式  M * v1， v1究竟会被变换成什么样子，或者说什么空间内呢？这要由矩阵 M决定： M中的各基向量代表的是什么空间，这个 v1就会被转换到什么空间。

 

这个结论可以很自然地扩推广到三维或者高维空间中，因为“ 向量分解与再合成”的规则在一般（欧几里得）几何学中是普遍适用的。

 

现在，麻麻再也不用担心我的“空间转换”能力啦。