【算法27】硬币面值组合问题

问题描述

　　假设我们有8种不同面值的硬币｛1，2，5，10，20，50，100，200｝，用这些硬币组合够成一个给定的数值n。例如n=200，那么一种可能的组合方式为 200 = 3 * 1 + 1＊2 + 1＊5 + 2＊20 + 1 * 50 + 1 * 100. 问总过有多少种可能的组合方式？ (这道题目来自著名编程网站ProjectEuler, 点击这里查看原题目) 类似的题目还有：

　　[华为面试题] 1分2分5分的硬币三种，组合成1角，共有多少种组合

　　[创新工厂笔试题] 有1分，2分，5分，10分四种硬币，每种硬币数量无限，给定n分钱，有多少中组合可以组成n分钱

问题分析

　　给定一个数值sum，假设我们有m种不同类型的硬币{V1, V2, ..., Vm}，如果要组合成sum，那么我们有

sum = x1 * V1 + x2 * V2 + ... + xm * Vm 

求所有可能的组合数，就是求满足前面等值的系数{x1, x2, ..., xm}的所有可能个数。

　　[思路1] 当然我们可以采用暴力枚举，各个系数可能的取值无非是x1 = {0, 1, ..., sum / V1}, x2 = {0, 1, ..., sum/ V2}等等。这对于硬币种类数较小的题目还是可以应付的，比如华为和创新工厂的题目，但是复杂度也很高O（sum/V1 * sum/V2 * sum/V3 * ...）

　　[思路2] 从上面的分析中我们也可以这么考虑，我们希望用m种硬币构成sum，根据最后一个硬币Vm的系数的取值为无非有这么几种情况，xm分别取｛0, 1, 2, ..., sum/Vm｝，换句话说，上面分析中的等式和下面的几个等式的联合是等价的。

sum = x1 * V1 + x2 * V2 + ... + 0 * Vm

sum = x1 * V1 + x2 * V2 + ... + 1 * Vm

sum = x1 * V1 + x2 * V2 + ... + 2 * Vm

...

sum = x1 * V1 + x2 * V2 + ... + K * Vm  

　　其中K是该xm能取的最大数值K = sum / Vm。可是这又有什么用呢？不要急，我们先进行如下变量的定义：

dp[i][sum] = 用前i种硬币构成sum 的所有组合数。

　　那么题目的问题实际上就是求dp[m][sum]，即用前m种硬币（所有硬币）构成sum的所有组合数。在上面的联合等式中：当xn=0时，有多少种组合呢？ 实际上就是前i-1种硬币组合sum，有dp[i-1][sum]种！ xn = 1 时呢，有多少种组合？ 实际上是用前i-1种硬币组合成(sum - Vm)的组合数，有dp[i-1][sum -Vm]种; xn =2呢， dp[i-1][sum - 2 * Vm]种，等等。所有的这些情况加起来就是我们的dp[i][sum]。所以：

dp[i][sum] = dp[i-1][sum - 0*Vm] + dp[i-1][sum - 1*Vm]

+ dp[i-1][sum - 2*Vm] + ... + dp[i-1][sum - K*Vm]; 其中K = sum / Vm

　　换一种更抽象的数学描述就是：

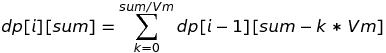
　　通过此公式，我们可以看到问题被一步步缩小，那么初始情况是什么呢？如果sum=0，那么无论有前多少种来组合0，只有一种可能，就是各个系数都等于0；

dp[i][0] = 1   // i = 0, 1, 2, ... , m

　　如果我们用二位数组表示dp[i][sum], 我们发现第i行的值全部依赖与i-1行的值，所以我们可以逐行求解该数组。如果前0种硬币要组成sum，我们规定为dp[0][sum] = 0. 

程序源码

　　通过上面的讨论，我们最终可以写出下面的代码来求解该类问题：

 1 /* 

 2  * Filename :coins.cpp

 3  * Description: solve coin combinations using dynamic programing

 4  * Complier: g++

 5  * Author: python27

 6  */

 7 #include <iostream>

 8 #include <string>

 9 #include <cmath>

10 #include <vector>

11 

12 using namespace std;

13 

14 /****************************************************************

15  * coin Combinations: using dynamic programming

16  *

17  * Basic idea:

18  * dp[i][j] = sum(dp[i-1][j-k*coins[i-1]]) for k = 1,2,..., j/coins[i-1]

19  * dp[0][j] = 1 for j = 0, 1, 2, ..., sum

20  * 

21  * Input:

22  * coins[] - array store all values of the coins

23  * coinKinds - how many kinds of coins there are

24  * sum - the number you want to construct using coins

25  *

26  * Output:

27  * the number of combinations using coins construct sum

28  *

29  * Usage:

30  * c[3] = {1, 2, 5};

31  * int result = coinCombinations(c, 3, 10);

32  *

33  ****************************************************************/

34 int coinCombinations(int coins[], int coinKinds, int sum)

35 {

36     // 2-D array using vector: is equal to: dp[coinKinds+1][sum+1] = {0};

37     vector<vector<int> > dp(coinKinds + 1);

38     for (int i = 0; i <= coinKinds; ++i)

39     {

40         dp[i].resize(sum + 1);

41     }

42     for (int i = 0; i <= coinKinds; ++i)

43     {

44         for (int j = 0; j <= sum; ++j)

45         {

46             dp[i][j] = 0;

47         }

48     }

49 

50     //init: dp[i][0] = 1; i = 0, 1, 2 ..., coinKinds

51     //Notice: dp[0][0] must be 1, althongh it make no sense that

52     //using 0 kinds of coins construct 0 has one way. but it the foundation

53     //of iteration. without it everything based on it goes wrong

54     for (int i = 0; i <= coinKinds; ++i)

55     {

56         dp[i][0] = 1;

57     }

58 

59     // iteration: dp[i][j] = sum(dp[i-1][j - k*coins[i-1]])

60     // k = 0, 1, 2, ... , j / coins[i-1]

61     for (int i = 1; i <= coinKinds; ++i)

62     {

63         for (int j = 1; j <= sum; ++j)

64         {

65             dp[i][j] = 0;

66             for (int k = 0; k <= j / coins[i-1]; ++k)

67             {

68                 dp[i][j] += dp[i-1][j - k * coins[i-1]];

69             }

70         }

71     }

72 

73     return dp[coinKinds][sum];

74 }

75 

76 int main()

77 {

78     int coins[8] = {1, 2, 5, 10, 20, 50, 100, 200};

79     int sum = 200;

80     int result = coinCombinations(coins, 8, 200);

81     cout << "using 8 kinds of coins construct 200, combinations are: " << endl;

82     cout << result << endl;

83     return 0;

84 }

 

　　聪明的读者或许已经发现，在算法的描述中说明用动态规划的方法来求解此问题，什么？动态规划，我们什么时候用动态规划了？哈哈，在我们写出递归公式并且给出初始解的时候，我们就已经在用动态规划了。

　　动态规划的基本思想就是将待求解问题分解为若干子问题，（如本题中我们将dp[i][j]分解为若干dp[i-1][j-x]的问题），先求解这些子问题并将结果保存起来( 我们用dp[][]二维数组保存子结果)，若在求解较大的问题时用到较小子问题的结果，可以直接取用(求dp[i][j]时用dp[i-1][x]的结果)，从而免去重复计算。动态规划是一种非常强大的算法思想，无论做过多少动态规划的题目，下一次依然会被动态规划的强大所震撼。随后的博客中，我们会更多的接触动态规划。你可以在后面的参考文献中找到更多有用的资源。 

参考文献

[1] ProjectEuler: http://projecteuler.net/problem=31

[2] Topcoder Algorithm tutorial: http://community.topcoder.com/tc?module=Static&d1=tutorials&d2=dynProg

[3] Sanjoy Dasgupta. 算法概论. 清华大学出版社，2008: 173 - 193.  

[4] Thomas H. Cormen, et al. 算法导论. 机械工业出版社，2011: 192 - 212.