湘潭校赛 Easy Wuxing

Easy Wuxing
Accepted : 25		Submit : 124
Time Limit : 1000 MS		Memory Limit : 65536 KB

 

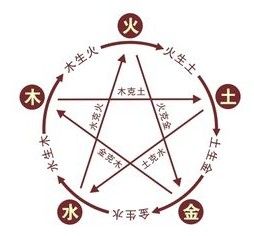
题目描述 “五行”是中国传统哲学思想，它认为认为大自然的现象由“木、火、土、金、水”这五种气的变化所总括， 不但影响到人的命运，同时也使宇宙万物循环不已。 五行具有相生相克的性质，规律如下： 五行相克：金克木，木克土，土克水，水克火，火克金。 五行相生：金生水，水生木，木生火，火生土，土生金。 五行任一行与其他五行的关系为：同我、生我、我生、克我、我克。 给你一个1*n的格子，将五行填上去，每格填一个，要求相邻格以及首尾格不能是同我和相克的关系， 请问一共有多少种不同的方案？   输入 多组样例，每组一个整数n(0≤n≤106)，如果n为0，表示输入结束，这个样例不需要处理。 输出 每行输出一个样例的结果，因为数值可能非常大，请将结果对109+7取模。 样例输入 1 2 0 样例输出 5 10 Source XTU OnlineJudge

[ Submit Solution ]

 

 

矩阵快速幂取模

  1 #include<iostream>

  2 #include<stdio.h>

  3 #include<cstring>

  4 #include<cstdlib>

  5 #include<queue>

  6 using namespace std;

  7 typedef __int64 LL;

  8 const LL mod = 1000000007;

  9 

 10 struct Matrix

 11 {

 12     LL mat[6][6];

 13     void Init()

 14     {

 15         LL cur;

 16         int i,j;

 17         mat[1][1]=0;mat[1][2]=0;mat[1][3]=1;mat[1][4]=1;mat[1][5]=0;

 18         for(i=2;i<=5;i++)

 19         {

 20             for(j=1;j<=5;j++)

 21             {

 22                 if(j==1) cur=5;

 23                 else cur=j-1;

 24                 mat[i][j]=mat[i-1][cur];

 25             }

 26         }

 27     }

 28 }M_hxl;

 29 void Matrix_ini(Matrix *cur,int n)

 30 {

 31     int i,j;

 32     for(i=1;i<=n;i++)

 33         for(j=1;j<=n;j++)

 34             if(i==j)

 35                 cur->mat[i][j]=1;

 36             else cur->mat[i][j]=0;

 37 }

 38 Matrix Multiply(Matrix cur,Matrix now,int len)

 39 {

 40     Matrix ww;

 41     int i,j,k;

 42     memset(ww.mat,0,sizeof(ww.mat));

 43     for(i=1;i<=len;i++)

 44     for(k=1;k<=len;k++)

 45     if(cur.mat[i][k])

 46     {

 47         for(j=1;j<=len;j++)

 48         if(now.mat[k][j])

 49         {

 50             ww.mat[i][j]+=cur.mat[i][k]*now.mat[k][j];

 51             if(ww.mat[i][j]>=mod)

 52             ww.mat[i][j]%=mod;

 53         }

 54     }

 55     return ww;

 56 }

 57 struct Matrix M_add(Matrix cur,Matrix now,int len)

 58 {

 59     Matrix ww;

 60     int i,j;

 61     memset(ww.mat,0,sizeof(ww.mat));

 62 

 63     for(i=1;i<=len;i++)

 64     for(j=1;j<=len;j++)

 65     {

 66         ww.mat[i][j]=cur.mat[i][j]+now.mat[i][j];

 67         if(ww.mat[i][j]>=mod)

 68         ww.mat[i][j]%=mod;

 69     }

 70     return ww;

 71 }

 72 Matrix pow_sum1(Matrix cur,int n,int len)

 73 {

 74     Matrix ww;

 75     Matrix_ini(&ww,len);

 76     while(n)

 77     {

 78         if(n&1)

 79         {

 80             ww=Multiply(ww,cur,len);

 81         }

 82         n=n>>1;

 83         cur=Multiply(cur,cur,len);

 84     }

 85     return ww;

 86 }

 87 void solve(int n)

 88 {

 89     LL k=0;

 90     M_hxl.Init();

 91     M_hxl=pow_sum1(M_hxl,n,5);

 92     k=(M_hxl.mat[1][3]+M_hxl.mat[1][4])%mod;

 93     k=(k*5)%mod;

 94     printf("%I64d\n",k);

 95 }

 96 int main()

 97 {

 98     LL T,n;

 99     while(scanf("%I64d",&n)>0)

100     {

101         if(n==0)break;

102         if(n==1)

103         {

104             printf("5\n");

105             continue;

106         }

107         solve(n-1);

108     }

109     return 0;

110 }