BestCoder 1st Anniversary 1004 Bipartite Graph 【二分图 + bfs + 良好的逻辑思维 】

题目地址： http://bestcoder.hdu.edu.cn/contests/contest_showproblem.php?cid=610&pid=1004

问题描述

Soda有一个$n$个点$m$条边的二分图, 他想要通过加边使得这张图变成一个边数最多的完全二分图. 于是他想要知道他最多能够新加多少条边. 注意重边是不允许的.

输入描述

输入有多组数据. 第一行有一个整数$T$ $(1 \le T \le 100)$, 表示测试数据组数. 然后对于每组数据:



第一行报包含两个整数$n$和$m$, $(2 \le n \le 10000, 0 \le m \le 100000)$.



接下来$m$行, 每行两个整数$u$和$v$$ (1 \le u, v \le n, v \ne u)$, 表示$u$和$v$之间有一条无向边.



输入保证给出的图是二分图, 没有重边, 没有自环. 大部分数据都是小数据.

输出描述

对于每组数据, 输出Soda最多能加的边数.

输入样例

2

4 2

1 2

2 3

4 4

1 2

1 4

2 3

3 4

输出样例

2

0

　　题目分析：题目我截取的是汉语页面，给你提个二分图，当然测试数据会保证它一定是一个二分图。现在想要给它加边变成一个边数最多完全二
分图。
完全二分图的样子如下：

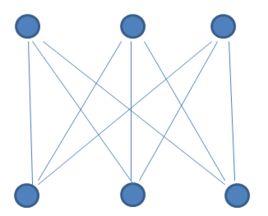
　　我们简单的假设：上边的点属于A集合，下面的点属于B集合。A集合中的每一个点都要与B集合中每一个点有边连接，并且集合内部之间的点是
没有边连接的，这样的图才是完全二分图。完全二分图的边数=A集合的点数*B集合的点数。

　　我们该如何解这个问题呢？ 
思路：因为测试数据会保证给出的图一定是一个二分图，我们可以通过一次bfs搜索，将图中的节点分成A、B两个集
合。此处需要注意的是并不一定所有的点都在图当中，也就是说有的节点可能是孤立的。我们需要把剩下的那些孤立的节点再分配到A、B集合当中去。
徐泽分配到那个集合需要一定的思考。此处先说明一个样例问题：给你一条一定长的线段，让它围成的矩形面积最大，怎么搞？当然是尽量的让它的
长和宽尽量相等接近正方形时最大啊！ 同理，如果我们要让这些节点组成一个最大的完全二分图，那就是尽量让两个集合的节点尽量一样多。通过
一次bfs搜索后就可以确定A、B节点的数量了，这是确定的，不能更改。我们只能通过剩下的那些孤立的节点（孤立的节点数目可能为0）来让A、B
两个集合点数尽量相同。至于怎么分配这剩下的孤立的节点数就不用细说了吧！

code:

#include <stdio.h>

#include <string.h>

#include <stdlib.h>

#include <math.h>

#include <ctype.h>

#include <iostream>

#include <queue>

#include <stack>

#include <vector>

#include <algorithm>

#define PI acos(-1.0);

#define N 10000+10

#define M 100000+10



using namespace std;



int n, m;

vector<int>q[N];

int flag[N];

bool vis[N];



void bfs(int dd)

{

    //0代表未着色，1代表白色，2代表黑色



    queue<int>p;

    while(!p.empty()) p.pop();

    p.push(dd);

    flag[dd]=1;

    vis[dd]=true;

    while(!p.empty())

    {

        int dd=p.front(); p.pop();



        for(int i=0; i<q[dd].size(); i++)

        {

            if(flag[q[dd][i]]==0 && vis[q[dd][i]]==false )

            {

                flag[q[dd][i]] = flag[dd]==1?2:1;

                p.push(q[dd][i]);

            }

        }

    }



}









int main()

{

    int tg;

    scanf("%d", &tg);



    int n;

    int i, j, k;



    while(tg--){

        scanf("%d %d", &n, &m);

        int u, v;



         for(i=1; i<=n; i++)

            q[i].clear();

        for(i=0; i<m; i++)

        {

            scanf("%d %d", &u, &v);

            q[u].push_back(v);

            q[v].push_back(u); //建立无向图

        }

        memset(flag, 0, sizeof(flag));

        memset(vis, false, sizeof(vis));



        bfs(1);

        int cnt1=0, cnt2=0;



        for(i=1; i<=n; i++)

            if(flag[i]==1 ) cnt1++;

        for(i=1; i<=n; i++)

            if(flag[i]==2) cnt2++;



        int aa=n-cnt1-cnt2; //aa是孤立节点数

        int bb=max(cnt1, cnt2)-min(cnt1, cnt2); //bb是两个集合的节点数之差



        if( aa <= bb ){

            int cc=min(cnt1, cnt2); cc=cc+aa;

            if(cnt1<=cnt2) cnt1=cc;

            else cnt2=cc;

        }

        else{

            int cc=min(cnt1, cnt2); cc=cc+bb;

            aa=aa-bb;

            if(cnt1<=cnt2) cnt1=cc;

            else cnt2=cc;



            cnt1=cnt1+aa/2;

            aa=aa-aa/2;

            cnt2=cnt2+aa;

        }

        printf("%d\n", cnt1*cnt2-m);

    }

    return 0;

}