八数码（双向广搜）

早上看了提到双向广搜的一篇文章，其中讲了双向广搜可以节约一半的时间和一半的空间（理论上），我画了一幅图：

（上面的对应普通BFS，下面的对应双向广搜）

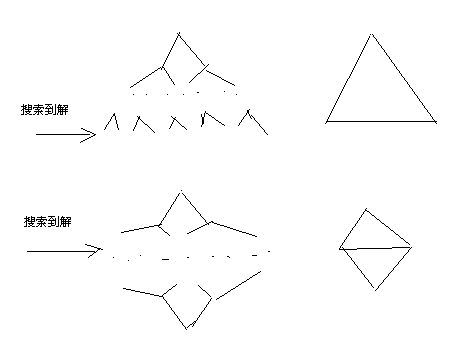
可以看出简单BFS的搜索节点大约是双向广搜的二倍。

对于八数码问题，由于逆序剪枝可以将所有无解的状态全部剪掉，剩余的都是有解的状态，所以使用双向广搜速度可能会更快；

对下面两组数据（分别输入）

1 2 3 4 5 6 7 8 0
8 7 6 5 4 3 2 1 0

2 6 4 1 3 7 0 5 8
8 1 5 7 3 6 4 0 2

正确输出对应是 30、 31

使用BFS的运行时间：0.390s  0.359s

使用双广的运行时间：0.109s 0.046s

双广我开始想按自己的思路来写，定义的是两个队列，两个vis[]，两个dist[]，最后发现根本运行不了（后来写后面的时才发现是将几个大的数组定义在了局部引起的），睡了一觉，看了这篇Poj 1915 - Knight Moves 双向广搜（Maxwell.O.Y），才对双广的结构有了新的理解；

  1 # include <stdio.h>

  2 # include <mem.h>

  3 

  4 # define MAXN (362880 + 5)

  5 

  6 typedef struct 

  7 {

  8     char a[9];

  9 }state;

 10 

 11 const int dir[4][2] = {{-1,0}, {0,1}, {1,0}, {0,-1}};

 12 int fact[9];

 13 

 14 int front, rear;

 15 state cur, nst;            /* new state */

 16 char vis[MAXN];

 17 char dist[MAXN];        /* 求的是最短距离( < 100)，可以用 char 类型 */

 18 state Q[MAXN/2];

 19 

 20 

 21 void read(state *s);

 22 int inversions(state s);

 23 int cantor(state s);

 24 void init_fact(void);

 25 int bfs_d(state start, state goal);

 26 

 27 int main()

 28 {

 29     state start, goal;

 30     

 31     freopen("in.txt", "r", stdin);

 32     freopen("out.txt", "w", stdout);

 33     

 34     init_fact();

 35 

 36     read(&start);

 37     read(&goal);

 38 

 39     if (inversions(start)%2 == inversions(goal)%2)

 40     {

 41         printf("%d\n", bfs_d(start, goal));

 42     }

 43     else puts("-1");

 44 

 45     return 0;

 46 }

 47 

 48 int bfs_d(state start, state goal)

 49 {

 50     int i, x, y, nx, ny, ct, nt;

 51 

 52     memset(vis, 0, sizeof(vis));

 53     memset(dist, 0, sizeof(dist));

 54 

 55     front = 1;

 56     Q[front] = start;

 57     rear = 2;

 58     Q[rear++] = goal;

 59     vis[cantor(start)] = 1;                /* 1 表示从起始节点扩展得到 */

 60     vis[cantor(goal)] = 2;                /* 2 表示从目标节点扩展得到 */

 61 

 62     while (front < rear)

 63     {

 64         cur = Q[front++];

 65         ct = cantor(cur);

 66         for (i = 0; cur.a[i] && i < 9; ++i) ;

 67         x = i / 3;

 68         y = i % 3;

 69         for (i = 0; i < 4; ++i)

 70         {

 71             nx = x + dir[i][0];

 72             ny = y + dir[i][1];

 73             if (nx>=0 && nx<3 && ny>=0 && ny<3)

 74             {

 75                 nst = cur;

 76                 nst.a[x*3+y] = cur.a[nx*3+ny];

 77                 nst.a[nx*3+ny] = 0;

 78                 if (!vis[nt = cantor(nst)])

 79                 {

 80                     Q[rear++] = nst;

 81                     /* foot[nt] = ct; */

 82                     dist[nt] = dist[ct] + 1;

 83                     vis[nt] = vis[ct];

 84                 }

 85                 else if (vis[ct] != vis[nt])

 86                 {

 87                     return 1 + dist[nt] + dist[ct];

 88                 }

 89             }

 90         }

 91     }

 92 

 93     return -1;

 94 }

 95 

 96 void read(state *s)

 97 {

 98     int i;

 99     char c[5];

100 

101     for (i = 0; i < 9; ++i)

102     {

103         scanf("%s", c);

104         if (c[0] == 'x') (*s).a[i] = 0;

105         else (*s).a[i] = c[0] - '0';

106     }

107 }

108 

109 int inversions(state s)

110 {

111     char ch;

112     int i, j, ret;

113 

114     ret = 0;

115     for (i = 0; i < 9; ++i)

116     {

117         if (s.a[i] == 0) continue;

118         ch = s.a[i];

119         for (j = i+1; j < 9; ++j)

120         {

121             if (s.a[j] < ch && s.a[j] != 0)

122                 ++ret;

123         }

124     }

125 

126     return ret;

127 }

128 

129 int cantor(state s)

130 {

131     char ch;

132     int i, j, ret, cnt;

133 

134     ret = 0;

135     for (i = 0; i < 9; ++i)

136     {

137         cnt = 0;

138         ch = s.a[i];

139         for (j = i+1; j < 9; ++j)

140         {

141             if (s.a[j] < ch)

142                 ++cnt;

143         }

144         ret += cnt*fact[8-i];

145     }

146 

147     return ret;

148 }

149 

150 void init_fact(void)

151 {

152     int i;

153 

154     fact[0] = 1;

155     for (i = 1; i < 9; ++i)

156     {

157         fact[i] = i * fact[i-1];

158     }

159 }

用到的主要有：逆序剪枝，康托展开，双向广搜（……第四层）。

********************************************

刚吃饭想到了一种比较不正常的提速方法，也是看了郭大侠的博客才考试考虑提速的：假设最短距离的最大值是31，相应扩展的节点为N的话，根据BFS的特点完全可以将队列缩小很多！试了试果然提速了不少：（对应上面的例子）15ms 31ms；

郭大侠提出了一种构造法（非最优解）可以在有限的步数内按照一定的规则构造出一个解，对于大多数输入，速度要比搜索要快一些。