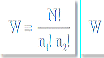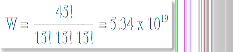Randomization Tests

Randomization Tests (1 of 6)

Most distribution-free tests are based on the principle of randomization. The best way to understand the principle of randomization is in terms of a specific example of a randomization test. Assume that four numbers are sampled from each of two populations. The numbers are shown below.

    Group 1        Group 2

       11          2

       14          9

        7          0

        8          5

  Mean 10          4

The first step is to compute the difference between means. For these data, the difference is six. The second step is to compute the number of ways these eight numbers could be divided into two groups of four. The general formula is:

where W is the number of ways, N is the total number of numbers (8 in this case), n₁is the size of the first group (4 in this case) and n₂ is the size of the second group (4 in this case). Therefore, W = 8!/(4! 4!) = 70.

Randomization Tests (2 of 6)

This means that there are 70 ways in which eight numbers can be divided into two groups of four.
The third step is to determine how many of these W ways of dividing the data result in differences between the means as large or larger than the difference obtained in the actual data. An examination of the data shows that there are only two ways the eight numbers can be divided into two groups of four with a larger difference between means than the difference of six found in the actual arrangement. These two ways are shown below.

Thus, including the original data, there are three ways in which the eight numbers can be arranged so that the difference between means is six or more.

Randomization Tests (3 of 6)

To compute the probability value for a one-tailed test of the difference between groups, divide this value of three by the W of ways of dividing the data into two groups of four. The probability value is therefore: p = 3/70 = 0.0429.
For a two-tailed test, the three cases in which Group 2 had a mean that was greater than Group 1 by six or more would be considered. This would make the two-tailed probability: p = 6/70 = 0.0857.
In summary, a randomization test proceeds from the data actually collected. It compares a computed statistic (the difference between means in this example) with the value of that statistic for other arrangements of the data. The probability value is simply the proportion of arrangements leading to a value of the statistic as large or larger than the value obtained from the actual data.

Randomization Tests (4 of 6)

Consider one more example of a randomization test. Suppose a researcher wished to know whether or not there were a relationship between two variables: X and Y. The most common way to test the relationship would be using Pearson's r.

 

 X  Y

 4  3

 8  5

 2  1

10  7

 9  8

The test based on the principle of randomization would proceed as follows. First, Pearson's correlation would be computed for the data as they stand. The value is: r = 0.9556. Next, the number of ways the X and Y numbers could be paired is calculated (Note that X's do not become Y's and Y's do not become X's. It is the pairings that change.) The formula for the number of ways that the numbers can be paired is simply:
W = N!
where N is the number of pairs of numbers. For this example, N = 5 and W = 120. This means there are 120 ways the numbers can be paired. Of these pairings, only one would produce a higher correlation than 0.9556. It is shown on the next page. Therefore, there are two ways of arranging the data that result in correlations of 0.9556 or higher.

  X   Y

  4   3

  8   5

  2   1

 10   8

  9   7


r = .981

This makes the one-tailed probability equal to: p = 2/120 = 0.017. Naturally, the two-tailed probability is 0.034.
Randomization tests have only one major drawback: they are impractical to compute with moderate to large sample sizes. For example, the number of ways 45 scores can be equally divided among three groups is which is an astronomical number. Even high-speed computers are incapable of the necessary calculations.

Randomization Tests (6 of 6)

Fortunately, there is an alternative computational method called "resampling." Instead of calculating all possible ways the data could be arranged, one can take numerous random samples from the set of possible arrangements. For the problem of dividing 45 numbers into three groups of 15 each, one could randomly select 10,000 of the possible arrangements and determine the proportion of these for which the effect size in the sample is exceeded. This proportion is then an accurate estimate of the probability level. This procedure is currently not in frequent use due, in part, to the general unavailability of programs to do this type of computation.

关键词：permutation tests, Randomization Tests, 置换检验，组合检验，排列检验

From:

http://davidmlane.com/hyperstat/B163479.html

http://davidmlane.com/hyperstat/B152250.html （Rank Randomization Tests）

http://davidmlane.com/hyperstat/index.html （HyperStat Online Statistics Textbook ）