读书笔记《数据挖掘概念与技术》第2章 数据预处理 2.6 数据离散化和概念分层产生
《数据挖掘:概念与技术(原书第2版)》
2.6 数据离散化和概念分层产生
通过将属性值划分为区间,数据离散化技术可以用来减少给定连续属性值的个数。区间的标记可以替代实际的数据值。用少数区间标记替换连续属性的数值,从而减少和简化了原来的数据。这导致挖掘结果的简洁、易于使用的、知识层面的表示。
离散化技术可以根据如何进行离散化加以分类,如根据是否使用类信息或根据进行方向(即自顶向下或自底向上)分类。如果离散化过程使用类信息,则称它为监督离散化(supervised discretization);否则是非监督的(unsupervised)。如果首先找出一点或几个点(称作分裂点或割点)来划分整个属性区间,然后在结果区间上递归地重复这一过程,则称它为自顶向下离散化或分裂。自顶向上离散化或合并正好相反,首先将所有的连续值看作可能的分裂点,通过合并相邻域的值形成区间,然后递归地应用这一过程于结果区间。可以对一个属性递归地进行离散化,产生属性值的分层或多分辨率的划分,称作概念分层。概念分层对于多个抽象层的挖掘是有用的。
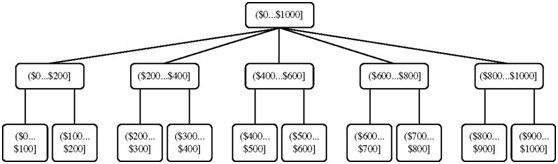
对于给定的数值属性,概念分层定义了该属性的一个离散化。通过收集较高层的概念(如青年、中年或老年)并用它们替换较低层的概念(如年龄的数值),概念分层可以用来规约数据。通过这种数据泛化,尽管细节丢失了,但是泛化后的数据更有意义、更容易解释。这有助于通常需要的多种挖掘任务的数据挖掘结果的一致表示。此外,与对大型未泛化的数据集挖掘相比,对规约的数据进行挖掘所需的I/O操作更少,并且更有效。正因为如此,离散化技术和概念分层作为预处理步骤,在数据挖掘之前而不是在挖掘过程进行。属性price的概念分层例子在图2-22给出。对于同一个属性可以定义多个概念分层,以适合不同的用户的需要。
对于用户或领域专家,人工地定义概念分层可能是一项令人乏味、耗时的任务。幸而,可以使用一些离散化方法来自动的产生或动态的提炼数值属性的概念分层。此外,许多分类属性的分层结构蕴含在数据库模式中,可以在模式定义级自动的定义。
2.6.1 数值数据的离散化和概念分层产生
对于数值属性说明概念分层是困难的和令人乏味的,这是由于数据的可能取值范围的多样性和数据值的更新频繁。这种人工地说明还可能非常随意。
数值属性的概念分层可以根据数据离散化自动构造。考察如下方法:分箱、直方图分析、基于熵的离散化、χ2合并、聚类分析和通过直观划分离散化。一般,每种方法都假定待离散化的值已经按递增序排序。
Ø 分箱
分箱是一种基于箱的指定个数自底向下的分裂技术。2.3.2节讨论了数据光滑的分箱方法。这些方法也可以用作数值规约和概念分层产生的离散化方法。例如,通过使用等宽或等频分箱,然后用箱均值或中位数替换箱中的每个值,可以将属性值离散化,就像分别用箱的均值或箱的中位数光滑一样。这些技术可以递归地作用于结果划分,产生概念分层。分箱并不使用类信息,因此是一种非监督的离散化技术。它对用户指定的箱个数很敏感,也容易受离群点的影响。
Ø 直方图分析
像分箱一样,直方图分析也是一种非监督离散化技术,因为它也不使用类信息。直方图将属性A的值划分成不相交的区间,称作桶。直方图已在2.2.3节介绍。定义直方图大划分规则已在2.5.4节介绍。例如,在等宽的直方图中,将值分成相等的划分或区间。使用等频直方图,理想地分割值使得每个划分包括相同个数大数据元组。直方图分析算法可以递归地用于每个划分,自动的产生多级概念分层,直到达到预先设定的概念层数过程终止。也可以对每一层使用最小区间长度来控制递归过程。最小区间长度设定每层每个划分的最小宽度,或每层每个划分中值的最少数目。正如下面介绍的那样,直方图也可以根据数据分布的聚类分析进行划分。
Ø 基于熵的离散化
熵(entropy)是最常用的离散化度量之一。它由Claude Shannon在信息论和信息增益概念的开创性工作中首次引进。基于熵的离散化是一种监督的、自定向下的分裂技术。它在计算和确定分裂点(划分属性区间的数据值)时利用类分布信息。为了离散数值属性A,该方法选择A的具有最小熵的值作为分裂点,并递归地划分结果区间,得到分层离散化。这种离散化形成A的概念分层。
设D由属性集和类标号属性定义的数据元组组成。类标号属性提供每个元组的类信息。该集合中属性A的基于熵的离散化基本方法如下:
(1) A的每个值都可以看作一个划分A的值域的潜在的区间边界或分裂点(记作split_point)。也就是说,A的分裂点可以将D中的元组划分成分别满足条件A≤split_point和A>split_point的两个子集,这样就创建了一个二元离散化。
(2) 正如上面提到的,基于熵的离散化使用元组的类标号信息。为了解释基于熵的离散化的基本思想,必须考察一下分类。假定要根据属性A和某分裂点上的划分将D中的元组分类。理想地,希望该划分导致元组的准确分类。例如,如果有两个类,希望类C1的所有元组落入一个划分,而类C2的所有元组落入另一个划分。然而,这不大可能。例如,一个划分可能包含许多C1的元组,但也包含某些C2的元组。在该划分之后,为了得到完全的分类,我们还需要多少信息?这个量称作基于A的划分对D的元组分类的期望信息需求,由下式给出:
![]()
其中,D1和D2分别对应于D中满足条件A≤split_point和A>split_point的元组,|D|是D中元组的个数,如此等等。给定集合的熵函数Entropy根据集合中元组的类分布来计算。例如,给定m个类C1,C2,……,Cm,D1的熵是

其中,pi时D1中类Ci类的元组数除以D1中的元组总数|D1|确定。这样,在选择属性A的分裂点时,我们希望选择产生最小期望信息需求(即min(InfoA(D)))的属性值。这将导致在用A≤split_point和A>split_point划分之后,对元组完全分类(还)需要的期望信息量最小。这等价于具有最大信息增益的属性-值对(这方面的进一步细节在第6章讨论分类式给出)。
(3) 确定分裂点的过程递归地用于所得到的每个分划,直到满足某个终止标准,如当所有候选分裂点上的最小信息需求小于一个小阈值ε,或者当区间的个数大于阈值max_interval时终止。
基于熵的离散化可以减少数据量。与迄今为止提到的其他方法不同,基于熵的离散化使用类信息。这使得它更有可能将区间边界(分裂点)定义在准确位置,有助于提高分类的准确性。这里介绍的熵和信息增益度量也用于决策树归纳。这些度量将在6.3.2节更详细地讨论。
Ø 基于χ2分析的区间合并
ChiMerge是一种基于χ2的离散化方法。到目前为止我们研究的离散化方法都使用自顶向下的分裂策略。ChiMerge正好相反,才用自底向上的策略,递归地找出最佳临近区间,然后合并它们,形成较大的区间。这种方法是监督的,它使用类信息。其基本思想是,对于精确的离散化,相对类频率在一个区间内应当相当一致。因此,如果两个临近的区间具有非常类似的类分布,则这两个区间可以合并。否则,它们应当保持分开。
ChiMerge过程如下。初始,将数值属性A点每个不同值看作一个区间。对每个相邻区间进行χ2检验。具有最小χ2值的相邻区间合并在一起,因为低χ2值表明它们具有相似的分布。该合并过程递归地进行,直到满足预先定义的终止标准。
终止判定标准通常由三个条件决定。首先,当所有相邻区间对的χ2值都低于由指定的显著水平确定的某个阈值时合并停止。χ2检验的置信水平值太高(或非常高)可能导致过分离散化,而太低(或非常低)点值可能导致离散化不足。通常,置信水平设在0.10~0.01之间。其次,区间数可能少于预先指定点max-interval,如10~15。最后,回想一下ChiMerge的前提是区间内相对类频率应当相当一致。实践中,某些不一致是允许的,尽管不应当超过某个预先指定的阈值,如3%,这可以由某训练数据估计。最后一个条件可以用来删除数据集中不相关的属性。
Ø 聚类分析
聚类分析是一种流行的数据离散化方法。通过将属性A的值划分成簇和组,聚类算法可以用来离散化数值属性A。聚类考虑A的分布以及数据点的邻近性,因此,可以产生高质量的离散化结果。遵循自顶向下的划分策略或自底向上的合并策略,聚类可以用来产生A的概念分层,其中每个簇形成概念分层的一个节点。在前者,每一个初始簇或划分可以进一步分解成若干子簇,形成较低的概念层。在后者,通过反复的对临近簇进行分组,形成较高的概念层。
Ø 通过直观划分离散化
尽管分箱、直方图、聚类和基于熵的离散化对于数值分层的产生是有用的,但是许多用户希望看到数值区域被划分为相对一致的、易于阅读、看上去直观或“自然”的区间。例如,更希望将年薪划分成象($50,000, $60,000]的区间,而不是象由某种复杂的聚类技术得到的($51263.98, $60872.34]那样。
3-4-5 规则可以用于将数值数据划分成相对一致、“自然的”区间。一般地,该规则根据最重要的数字上的值区域,递归地、逐层地将给定的数据区域划分为3、4 或5 个相对等宽的区间。该规则如下:
l 如果一个区间在最重要的数字上包含3、6、7 或9 个不同的值,则将该区间划分成3 个区间(对于3、6 和9,划分成3 个等宽的区间;而对于7,按2-3-2 分组,划分成3 个区间);
l 如果它在最重要的数字上包含2、4 或8 个不同的值,则将区间划分成4 个等宽的区间;
l 如果它在最重要的数字上包含1、5 或10 个不同的值,则将区间划分成5 个等宽的区间。
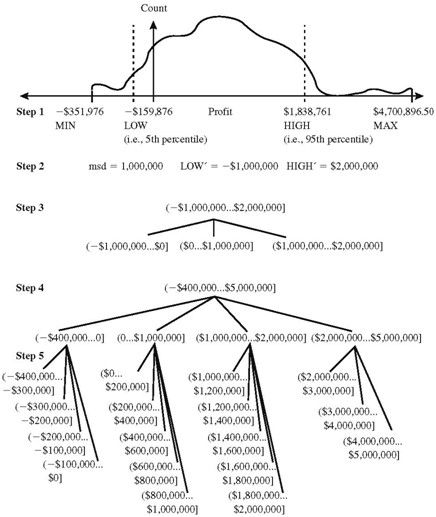
该规则可以递归地用于每个区间,为给定的数值属性创建概念分层。由于在数据集中可能有特别大的正值和负值,最高层分段简单地按最小和最大值可能导致扭曲的结果。例如,在资产数据集中,少数人的资产可能比其他人高几个数量级。按照最高资产值分段可能导致高度倾斜的分层。这样,顶层分段可以根据代表给定数据大多数的数据区间(例如,第5 个百分位数到第95 个百分位数)进行。越出顶层分段的特别高和特别低的值将用类似的方法形成单独的区间。
例2-6 根据直观划分产生数值概念分层。
2.6.2 分类数据的概念分层产生
分类数据是离散数据。分类属性具有有限个(但可能很多)不同值,值之间无序。例子包括地理位置、工作类别和商品类型。有很多方法产生分类数据的概念分层。
由用户或专家在模式级显式地说明属性的偏序:通常,分类属性或维的概念分层涉及一组属性。用户或专家在模式级通过说明属性的偏序或全序,可以很容易地定义概念分层。
通过显式数据分组说明分层结构的一部分:这基本上是人工地定义概念分层结构的一部分。在大型数据库中,通过显式的值枚举定义整个概念分层是不现实的。然而,对于一小部分中间层数据,我们可以很容易地显式说明分组。
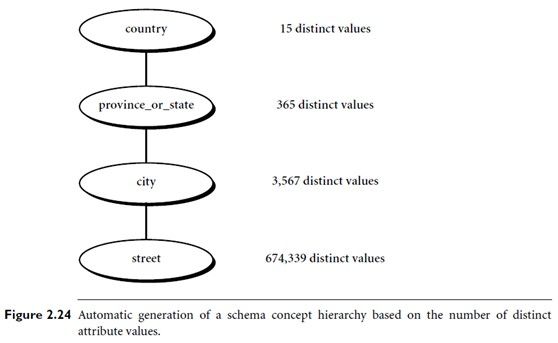
说明属性集但不说明它们的偏序:用户可以说明一个属性集形成概念分层,但并不显式说明它们的偏序。然后,系统可以尝试自动地产生属性的序,构造有意义的概念分层。“没有数据语义的知识,如何找出任意的分类属性集的分层序?”考虑下面的事实:由于一个较高层的概念通常包含若干从属的较低层概念,定义在高概念层的属性(如country)与定义在较低概念层的属性(如street)相比,通常包含少数数目的不同值。根据这一事实,可以根据给定属性集中每个属性不同值的个数自动地产生概念分层。具有最多不同值的属性放在分层结构的最低层。一个属性的不同值个数越少,它在所产生的概念分层结构中所处的层次越高。在许多情况下,这种启发式规则都很顶用。在考察了所产生的分层之后,如果必要局部层次交换或调整可以由用户或专家来做。
例2-7 根据每个属性的不同值的个数产生概念分层。假定用户对于AllElectronics 的维location 选定了属性集:street, country, province_or_state和city,但没有指出这些属性之间的层次序。
location 的概念分层可以自动地产生,如图2-24所示。首先,根据每个属性的不同值个数,将属性按降序排列,其结果如下(其中,每个属性的不同值数目在括号中):country(15), province_or_state(365),city(3567),street(674 339)。其次,按照排好的次序,自顶向下产生分层,第一个属性在最顶层,最后一个属性在最底层。最后,用户考察所产生的分层,必要时,修改它,以反映期望属性之间期望的语义联系。在这个例子中,显然不需要修改产生的分层。
注意,这种启发式规则并非完美无缺的。例如,数据库中的时间维可能包含20 个不同的年,12 个不同的月,每星期7 个不同的天。然而,这并不意味时间分层应当是“year < month < days_of_the_week”, days_of_the_week 在分层结构的最顶层。
只说明部分属性集:在定义分层时,有时用户可能不小心,或者对于分层结构中应当包含什么只有很模糊的想法。结果,用户可能在分层结构说明中只包含了相关属性的一小部分。为了处理这种部分说明的分层结构,重要的是在数据库模式中嵌入数据语义,使得语义密切相关的属性能够捆在一起。用这种办法,一个属性的说明可能触发整个语义密切相关的属性组“拖进”,形成一个完整的分层结构。然而必要时,用户应当可以选择忽略这一特性。
例2-8 使用预先定义的语义关系产生概念分层。假定数据挖掘专家(作为管理者)已将五个属性性number,street,city,province_or_state和country 捆绑在一起,因为它们关于location概念语义密切相关。如果用户在定义location 的分层结构时只说明了属性city,系统可以自动地拖进以上五个语义相关的属性,形成一个分层结构。用户可以选择去掉分层结构中的任何属性,如number和street,让city 作为该分层结构的最低概念层。