「2012-12-29」3x3手机锁屏矩阵图像的组合数量

这个问题，起源于@lzprgmr 的一个想法。「开手机的手势锁时想到个题，三乘三矩阵一共有几种手势？ 注意手势是有向的，且不能重复访问同一节点。」

特地拿着手机试了下，型号是华为的荣耀+，系统是安卓的4.0.4，应该不算是非主流的型号，图像锁屏的方式也应该还是主流的。主要特征如下。

1. 3x3的矩阵，手势划过的节点数量，不得低于4个，否则不算是合理的手势。
2. 对于如下的矩阵：2-1-3 和 2-3-1 是两种不同的手势。
   
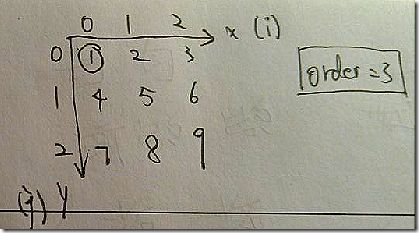
3. 无法从1跨越2直接到达3，同理，也无法跨越5直接到达9。即，由于手指的动作是连续的，无法跳跃选择数字，最后的手势动作，也必然形成一条连续的线段。（这里把「东」和「西」搞反了…… 不过无所谓了…… 囧）
   

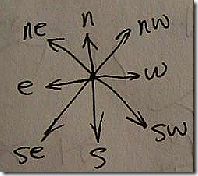
根据这样的特征，写了段程序，算出了相应的结果。大致的思路还是深度优先搜索（DFS），但是增加了一些较为特别的地方，比如用于保存当前矩阵状态（matrixState）的结构体。

struct gridAndState {

    struct gridPosition gPos;

    short currState[MATRIX_ORDER][MATRIX_ORDER];

    int visitedGridsCount; 



    gridAndState(struct gridPosition& pos)

        : gPos(pos)

    {

        saveCurrentMatrixState(currState);

        visitedGridsCount = matrixVisitedGridsCount();

    } 



    gridAndState(const struct gridAndState& gas)

        : gPos(gas.gPos), visitedGridsCount(gas.visitedGridsCount)

    {

        memcpy(this->currState, gas.currState, sizeof(gas.currState));

    }

};

而在搜索中，采取的就是上述结构体的栈。

std::vector<struct gridAndState> gridStack;

另外，对于上述提到的「由于手指的动作是连续的，无法跳跃选择数字」的特点，特地实现了一个 findAdjacentGrids 函数，比如如下的代码段，就是朝北边搜索相邻节点。

// Search adjacent grid from 8 directions:

// 1. north

for (x=srcX, y=srcY-1; isValidGridPosition(x, y); --y) {

    if (! gl_matrixState[x][y]) {

        struct gridPosition pos_(x, y);

        adjGrids.push_back(pos_);

        break;

    }

}

文件结构如下。

 

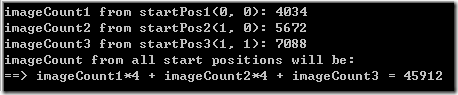
最后得到的结果是，48种（2x2，假设要求手势动作划过的节点数，大于等于3），45912（3x3，假设大于等于4，见下图），1117373296（4x4，假设大于等于5）。

可以拿2x2的结果验证一下，由于四个顶点等价，假设从西北角的顶点出发，如下所示，正好是12种，再乘以4个等价顶点，就是48种了。

代码待会放到 Github 上去，目前暂时还没账号，等会了解一下先。也可以先直接从新浪微盘里下载。