poj1487

题目大意： 给一棵递归树，看链接图片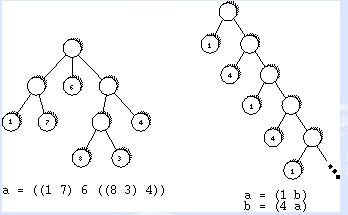，从根节点开始对于每个节点往它的子节点移动，直到叶子节点停止。每个节点选哪一个孩子节点继续往下走是随机的(等概率)。然后叶子节点都会标记一个数值，记为走到该节点的得分。

输入条件：先输入整数n(n=0时结束),接下来有n行(n <= 26)，每一行会为前n个小写字母(每个字母作为一个变量)的描述。如a = (1 b)表示 f(a) = 1/2 * (1 + f(b))其中f(x)为x节点的得分期望。

现在对n个小写字母表示的变量节点，求出那个节点的得分期望即f(x) (x=a,b,c ...)。

 

这个题相当有意思，有意思在于它的输入——基于某个字符集的语义分析。递归向下分析的策略，而且是非常典型LL(1)文法！

S -> XWEWT

X -> (X)|a|b|c|...|z

E -> '='

W -> {Blank}|空

T -> (U)

U -> T|X|I

U -> UwU

w ->  {Blank}

I -> [+|-]{Digit}+[.{Digit}]

这道题另外一个关键点是将T转化成方程式，然后综合这n个方程式，使用gauss消元求解。

gauss消元其实就是线性代数中，化简行列式然后进行求解。不会的亲们回去好好看看线性代数的书，不要看网上某些人写的不清不楚的报告。

只是有一点需要注意：计算机中的数字是有界的，要时刻注意数字边界问题！

还有，很多事情需要自己亲身实践，我贡献了很多次WA，一个大原因是听人家要排除输出"-0.000"的问题。

  1 #include <iostream>

  2 #include <cstring>

  3 #include <cstdio>

  4 #include <queue>

  5 #include <algorithm>

  6 #include <cstdlib>

  7 #include <cmath>

  8 using namespace std;

  9 int alpha[128]={0},n;

 10 int getint(char *mes){

 11     int i=0;

 12     while(mes[i]!='\0' && (mes[i]<'0' || mes[i]>'9')) i++;

 13     return atoi(mes+i);

 14 }

 15 struct equation{

 16     double ec[27];

 17     equation(){ for(int i=0;i<27;i++) ec[i]=0; }

 18     equation operator+(const equation & S){ equation E; for(int i=0;i<27;i++) E.ec[i]= ec[i]+S.ec[i];  return E; }

 19     equation operator+=(const equation & S){ for(int i=0;i<27;i++) ec[i]+=S.ec[i];  return *this; }

 20     equation operator*(double rat){ equation E; for(int i=0;i<27;i++) E.ec[i]= ec[i]*rat;  return E; }

 21     void print(){ for(int i=0;i<n-1;i++) printf("%f*%c + ",ec[i],i+'a'); printf("%f*%c = %f\n",ec[n-1],n-1+'a',ec[26]); }

 22 };

 23 char mes[1010000]; int idx;

 24 equation getEquation(){

 25     equation E;

 26     if(mes[idx] == '('){

 27         queue<equation> que; idx++;

 28         while(1){

 29             while(!alpha[mes[idx]]) idx++; //跳到下一个合法字母

 30             if(mes[idx]==')') break;

 31             que.push(getEquation());

 32         } idx++;

 33         double quesize=1.0/que.size();

 34         while(!que.empty()) E += que.front()*quesize, que.pop();

 35     }else if(mes[idx]>='0'&&mes[idx]<='9' || mes[idx]=='-' || mes[idx]=='+'){

 36         double t=0,sign=1;

 37         if(mes[idx]=='-' || mes[idx]=='+'){

 38             if(mes[idx]=='-') sign=-1;

 39             idx++;

 40         }

 41         while(mes[idx]>='0'&&mes[idx]<='9'){

 42             t = t*10 + mes[idx]-'0';

 43             idx++;

 44         }

 45         if(mes[idx]=='.'){

 46             double tt=0.1; idx++;

 47             while(mes[idx]>='0'&&mes[idx]<='9'){

 48                 t += tt*(mes[idx]-'0');

 49                 tt *= 0.1; idx++;

 50             }

 51         }

 52         //printf("t = %f, sign = %f\n",t,sign);

 53         E.ec[26]=t*sign;

 54     }else { // 'a' ---- 'z'

 55         E.ec[mes[idx]-'a']=1;

 56         idx++;

 57     }

 58     while(!alpha[mes[idx]]) idx++; //跳到下一个合法字母

 59     return E;

 60 }

 61 equation parse(){

 62     while(mes[idx]<'a' || mes[idx]>'z') idx++;

 63     int c=mes[idx]-'a';

 64     while(mes[idx]!='=') idx++; idx++;

 65     while(!alpha[mes[idx]]) idx++; //跳到下一个合法字母

 66     equation E = getEquation();

 67     E.ec[26]=-E.ec[26];

 68     E.ec[c]-=1;

 69     return E;

 70 }

 71 double mat[26][27];

 72 int setted[26],rid[26];

 73 const double zero=1e-10;

 74 void unset(int x){

 75     if(!setted[x]) return;

 76     setted[x]=0;

 77     for(int i=x-1;i>=0;i--)

 78     if(fabs(mat[i][x]) > zero)

 79         unset(i);

 80 }

 81 void gauss(){

 82     memset(setted,-1,sizeof(setted));

 83     for(int r=0;r<n;r++){

 84         int c=r;

 85         int nonzero=-1; double minv=1e99;

 86         for(int i=c;i<n;i++)

 87         if(fabs(mat[i][c]) > zero && fabs(mat[i][c]-1) < minv)

 88             nonzero=i, minv=mat[i][c];

 89         if(nonzero < 0) unset(r);

 90         else {

 91             double rat=1/mat[nonzero][c];

 92             for(int i=c;i<=n;i++) mat[nonzero][i] *= rat, swap(mat[nonzero][i],mat[r][i]);

 93             for(int i=0;i<n;i++)

 94             if(i!=r && fabs(mat[i][c]) > zero){

 95                 rat = mat[i][c];

 96                 for(int j=c;j<=n;j++)

 97                     mat[i][j] -= rat*mat[r][j];

 98             }

 99         }

100     }

101 }

102 int main()

103 {

104 // init the legal alpha

105     for(int i='0';i<='9';i++) alpha[i]=1;

106     for(int i='a';i<='z';i++) alpha[i]=1;

107     alpha['.']=1; alpha['(']=1; alpha[')']=1;

108     alpha['+']=1; alpha['-']=1;

109 // main logic

110     int game=1;

111     do {

112         gets(mes); n=getint(mes);

113         if(n <= 0) break;

114         for(int i=0;i<n;i++){

115             gets(mes); idx=0;

116             equation E = parse();

117             //E.print();

118             for(int j=0;j<27;j++)

119                 mat[i][j]=E.ec[j];

120         }

121         for(int j=0;j<n;j++)

122              mat[j][n]=mat[j][26];

123         printf("Game %d\n",game++);

124         gauss();

125         for(int j=0;j<n;j++)

126         if(setted[j]) {

127             /* 排除输出 -0.000 的问题， 这里多余了

128             int tt=0;

129             for(int i=0;i<n;i++){

130                 sprintf(mes,"%.3f",mat[j][n]);

131                 tt=0;

132                 if(memcmp("-0.000",mes,5)==0) tt=1;

133                 printf("Expected score for %c = %s\n",j+'a',mes+tt);

134             }

135             */

136             printf("Expected score for %c = %.3f\n",j+'a',mat[j][n]);

137         }

138         else printf("Expected score for %c undefined\n",j+'a');

139         puts("");

140     }while(1);

141     return 0;

142 }

View Code