AVL树的python实现
AVL树是带有平衡条件的二叉查找树,一般要求每个节点的左子树和右子树的高度最多差1(空树的高度定义为-1)。
在高度为h的AVL树中,最少的节点数S(h)由S(h)=S(h-1)+S(h-2)+1得出,其中S(0)=1,S(1)=2。
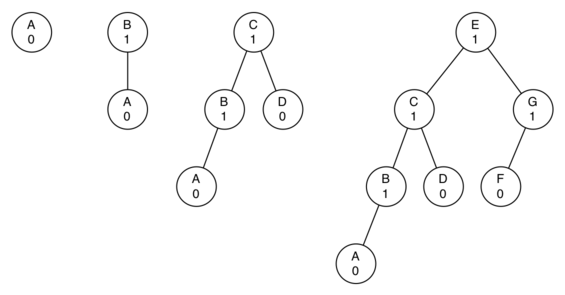
如上图,分别为高度为0,1,2,3的AVL树所需要的最少节点数。
1.AVL树的实现,遍历与查找操作与二叉查找树相同。
class Node(object):
def __init__(self,key):
self.key=key
self.left=None
self.right=None
self.height=0
class AVLTree(object):
def __init__(self):
self.root=None
def find(self,key):
if self.root is None:
return None
else:
return self._find(key,self.root)
def _find(self,key,node):
if node is None:
return None
elif key<node.key:
return self._find(key,self.left)
elif key>node.key:
return self._find(key,self.right)
else:
return node
def findMin(self):
if self.root is None:
return None
else:
return self._findMin(self.root)
def _findMin(self,node):
if node.left:
return self._findMin(node.left)
else:
return node
def findMax(self):
if self.root is None:
return None
else:
return self._findMax(self.root)
def _findMax(self,node):
if node.right:
return self._findMax(node.right)
else:
return node
def height(self,node):
if node is None:
return -1
else:
return node.height
2.AVL树的插入操作
插入一个节点可能会破坏AVL树的平衡,可以通过旋转操作来进行修正。
插入一个节点后,只有从插入节点到根节点的路径上的节点的平衡可能被改变。我们需要找出第一个破坏了平衡条件的节点,称之为K。K的两颗子树的高度差2。
不平衡有四种情况:
1.对K的左儿子的左子树进行一次插入
2.对K的左儿子的右子树进行一次插入
3.对K的右儿子的左子树进行一次插入
4.对K的右儿子的右子树进行一次插入
情况1与4是对称的,需要进行一次单旋转操作,清况2与3需要一次双旋转操作。
情况1:
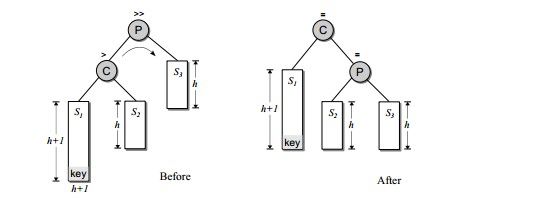
def singleLeftRotate(self,node):
k1=node.left
node.left=k1.right
k1.right=node
node.height=max(self.height(node.right),self.height(node.left))+1
k1.height=max(self.height(k1.left),node.height)+1
return k1
情况4:
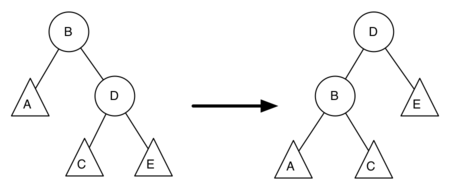
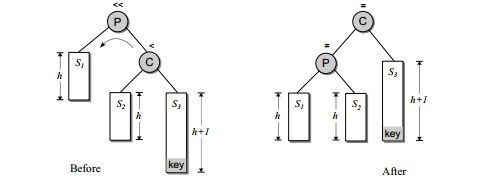
def singleRightRotate(self,node):
k1=node.right
node.right=k1.left
k1.left=node
node.height=max(self.height(node.right),self.height(node.left))+1
k1.height=max(self.height(k1.right),node.height)+1
return k1
情况3:
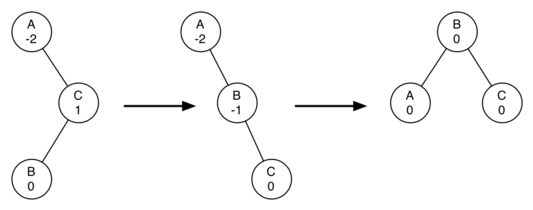
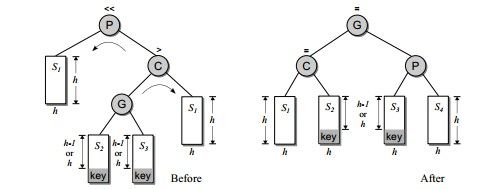
相当于进行了两次单旋转。
def doubleRightRotate(self,node):
node.right=self.singleLeftRotate(node.right)
return self.singleRightRotate(node)
情况2:
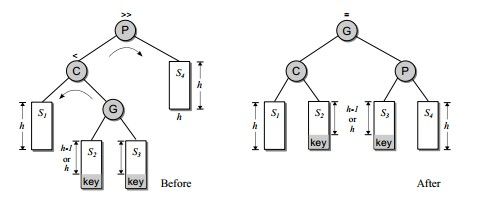
与情况3类似,都是进行了2次单旋转。
def doubleLeftRotate(self,node):
node.left=self.singleRightRotate(node.left)
return self.singleLeftRotate(node)
一系列插入操作:
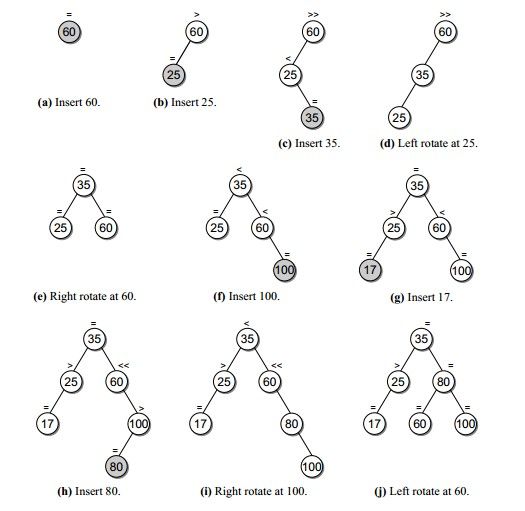
插入代码如下:
def put(self,key):
if not self.root:
self.root=Node(key)
else:
self.root=self._put(key,self.root)
def _put(self,key,node):
if node is None:
node=Node(key)
elif key<node.key:
node.left=self._put(key,node.left)
if (self.height(node.left)-self.height(node.right))==2:
if key<node.left.key:
node=self.singleLeftRotate(node)
else:
node=self.doubleLeftRotate(node)
elif key>node.key:
node.right=self._put(key,node.right)
if (self.height(node.right)-self.height(node.left))==2:
if key<node.right.key:
node=self.doubleRightRotate(node)
else:
node=self.singleRightRotate(node)
node.height=max(self.height(node.right),self.height(node.left))+1
return node
3.AVL树的删除操作:
删除操作比较复杂,如有错误,请指正。
1.当前节点为要删除的节点且是树叶(无子树),直接删除,当前节点(为None)的平衡不受影响。
2.当前节点为要删除的节点且只有一个左儿子或右儿子,用左儿子或右儿子代替当前节点,当前节点的平衡不受影响。
3.当前节点为要删除的节点且有左子树右子树:如果右子树高度较高,则从右子树选取最小节点,将其值赋予当前节点,然后删除右子树的最小节点。如果左子树高度较高,则从左子树选取最大节点,将其值赋予当前节点,然后删除左子树的最大节点。这样操作当前节点的平衡不会被破坏。
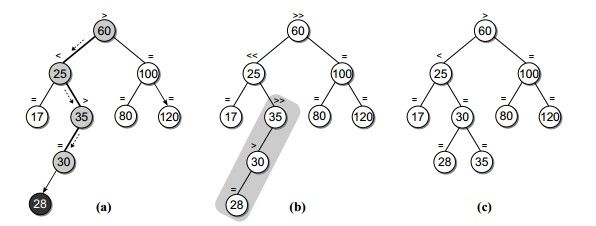
4.当前节点不是要删除的节点,则对其左子树或者右子树进行递归操作。当前节点的平衡条件可能会被破坏,需要进行平衡操作。
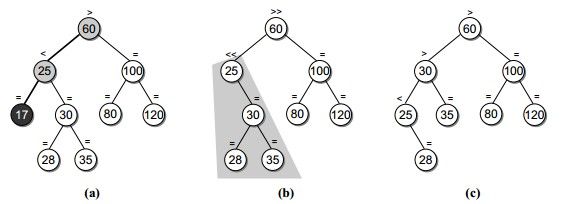
如上图,25为当前节点,左子树删除17后平衡条件被破坏,需要根据当前节点(25)的右子树(30)的左子树(28)高度是否高于右子树(35)的高度进行判断,若高于,进行双旋转,否则进行单旋转
def delete(self,key):
self.root=self.remove(key,self.root)
def remove(self,key,node):
if node is None:
raise KeyError,'Error,key not in tree'
elif key<node.key:
node.left=self.remove(key,node.left)
if (self.height(node.right)-self.height(node.left))==2:
if self.height(node.right.right)>=self.height(node.right.left):
node=self.singleRightRotate(node)
else:
node=self.doubleRightRotate(node)
node.height=max(self.height(node.left),self.height(node.right))+1
elif key>node.key:
node.right=self.remove(key,node.right)
if (self.height(node.left)-self.height(node.right))==2:
if self.height(node.left.left)>=self.height(node.left.right):
node=self.singleLeftRotate(node)
else:
node=self.doubleLeftRotate(node)
node.height=max(self.height(node.left),self.height(node.right))+1
elif node.left and node.right:
if node.left.height<=node.right.height:
minNode=self._findMin(node.right)
node.key=minNode.key
node.right=self.remove(node.key,node.right)
else:
maxNode=self._findMax(node.left)
node.key=maxNode.key
node.left=self.remove(node.key,node.left)
node.height=max(self.height(node.left),self.height(node.right))+1
else:
if node.right:
node=node.right
else:
node=node.left
return node
全部代码:
class Node(object):
def __init__(self,key):
self.key=key
self.left=None
self.right=None
self.height=0
class AVLTree(object):
def __init__(self):
self.root=None
def find(self,key):
if self.root is None:
return None
else:
return self._find(key,self.root)
def _find(self,key,node):
if node is None:
return None
elif key<node.key:
return self._find(key,self.left)
elif key>node.key:
return self._find(key,self.right)
else:
return node
def findMin(self):
if self.root is None:
return None
else:
return self._findMin(self.root)
def _findMin(self,node):
if node.left:
return self._findMin(node.left)
else:
return node
def findMax(self):
if self.root is None:
return None
else:
return self._findMax(self.root)
def _findMax(self,node):
if node.right:
return self._findMax(node.right)
else:
return node
def height(self,node):
if node is None:
return -1
else:
return node.height
def singleLeftRotate(self,node):
k1=node.left
node.left=k1.right
k1.right=node
node.height=max(self.height(node.right),self.height(node.left))+1
k1.height=max(self.height(k1.left),node.height)+1
return k1
def singleRightRotate(self,node):
k1=node.right
node.right=k1.left
k1.left=node
node.height=max(self.height(node.right),self.height(node.left))+1
k1.height=max(self.height(k1.right),node.height)+1
return k1
def doubleLeftRotate(self,node):
node.left=self.singleRightRotate(node.left)
return self.singleLeftRotate(node)
def doubleRightRotate(self,node):
node.right=self.singleLeftRotate(node.right)
return self.singleRightRotate(node)
def put(self,key):
if not self.root:
self.root=Node(key)
else:
self.root=self._put(key,self.root)
def _put(self,key,node):
if node is None:
node=Node(key)
elif key<node.key:
node.left=self._put(key,node.left)
if (self.height(node.left)-self.height(node.right))==2:
if key<node.left.key:
node=self.singleLeftRotate(node)
else:
node=self.doubleLeftRotate(node)
elif key>node.key:
node.right=self._put(key,node.right)
if (self.height(node.right)-self.height(node.left))==2:
if key<node.right.key:
node=self.doubleRightRotate(node)
else:
node=self.singleRightRotate(node)
node.height=max(self.height(node.right),self.height(node.left))+1
return node
def delete(self,key):
self.root=self.remove(key,self.root)
def remove(self,key,node):
if node is None:
raise KeyError,'Error,key not in tree'
elif key<node.key:
node.left=self.remove(key,node.left)
if (self.height(node.right)-self.height(node.left))==2:
if self.height(node.right.right)>=self.height(node.right.left):
node=self.singleRightRotate(node)
else:
node=self.doubleRightRotate(node)
node.height=max(self.height(node.left),self.height(node.right))+1
elif key>node.key:
node.right=self.remove(key,node.right)
if (self.height(node.left)-self.height(node.right))==2:
if self.height(node.left.left)>=self.height(node.left.right):
node=self.singleLeftRotate(node)
else:
node=self.doubleLeftRotate(node)
node.height=max(self.height(node.left),self.height(node.right))+1
elif node.left and node.right:
if node.left.height<=node.right.height:
minNode=self._findMin(node.right)
node.key=minNode.key
node.right=self.remove(node.key,node.right)
else:
maxNode=self._findMax(node.left)
node.key=maxNode.key
node.left=self.remove(node.key,node.left)
node.height=max(self.height(node.left),self.height(node.right))+1
else:
if node.right:
node=node.right
else:
node=node.left
return node