Floyd算法思想及实现
Floyd算法用于求每一对顶点间的最短距离。与Dijkstra算法相比较,时间复杂度均为O(n2),但Floyd算法形式上更简单一些。
一、 Floyd算法的原理
首先记录两点间无其他中间顶点的距离(Vi---Vj),加一个顶点为中间点,记录加一个顶点后两点间的最短距离,以此类推,加完N个顶点后两点间的最短距离即可求出。
二、算法实现
用三重循环实现。用二维数组表示顶点到顶点的距离。如D[i][j]表示从i到j点的距离。第一层循环依次加顶点,第二层循环遍历Vi点,第三层循环遍历Vj点。
/*graph.h文件*/ //---------图的数组(邻接矩阵)存储表示---------- #include<stdio.h> #include <string.h> #include <stdlib.h> #define INFINITY 10000 //最大值 #define MAX_VERTEX_NUM 20 //最大顶点个数 typedef int VRType; typedef char VertexType; typedef char InfoType; typedef enum{DG,DN,UDG,UDN} GraphKind; //有向图,有向网,无向图,无向网 typedef struct ArcCell { VRType adj; //顶点关系类型,对无权图,有1或0表示是否相邻;对带权图,则为权值类型。 InfoType *info; //弧相关信息的指针 }ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; typedef struct { VertexType vexs[MAX_VERTEX_NUM]; //顶点向量 AdjMatrix arcs; //邻接矩阵 int vexnum,arcnum; //图的当前顶点数和弧数 }mgraph,*MGraph; int Locate_vexs(MGraph &g,VertexType v) //定位顶点位置 { for (int i=0;i<g->vexnum;i++) if (g->vexs[i]==v) return i; return -1; } void Print_mgraph(MGraph &g) //打印图 { int i; printf("邻接矩阵为:\n"); printf("┏ "); //五个空格 for (i=0;i<g->vexnum;i++) printf("%c ",g->vexs[i]); printf("\n\n"); for (i=0;i<g->vexnum;i++) { printf("%c ",g->vexs[i]); for (int j=0;j<g->vexnum;j++) { //输出矩阵,并且调整矩阵 if (g->arcs[i][j].adj>0&&g->arcs[i][j].adj<10) printf("%d ",g->arcs[i][j].adj); else if (g->arcs[i][j].adj>9&&g->arcs[i][j].adj<100) printf("%d ",g->arcs[i][j].adj); else if (g->arcs[i][j].adj>99&&g->arcs[i][j].adj<1000) printf("%d ",g->arcs[i][j].adj); else if (g->arcs[i][j].adj>999&&g->arcs[i][j].adj<10000) printf("%d ",g->arcs[i][j].adj); else if(g->arcs[i][j].adj==INFINITY) printf("∞ "); } printf("\n\n"); } } void Add_vexs(MGraph &g) //增加顶点 { printf("请输入顶点个数:"); scanf("%d",&g->vexnum); getchar();//吸收回车符 printf("请输入顶点字符串序列:"); for (int i=0;i<g->vexnum;i++) scanf("%c",&g->vexs[i]); } void Add_arcs(MGraph &g) //增加边 { printf("请输入边的条数:"); scanf("%d",&g->arcnum); VertexType v1,v2; int row,col; VRType weight;; printf("请输入权重和对应顶点,以空格隔开:\n"); for (int i=0;i<g->arcnum;i++) { scanf("%d %c %c",&weight,&v1,&v2); row=Locate_vexs(g,v1); col=Locate_vexs(g,v2); g->arcs[row][col].adj=weight; } } void Init_graph(MGraph &g) //初始化图 { g=(MGraph)malloc(sizeof(mgraph)); g->vexnum=0; g->arcnum=0; for (int i=0;i<MAX_VERTEX_NUM;i++) g->vexs[i]='0'; for (i=0;i<MAX_VERTEX_NUM;i++) for (int j=0;j<MAX_VERTEX_NUM;j++) { g->arcs[i][j].adj=INFINITY; g->arcs[i][j].info=NULL; } } void Create_mgraph(MGraph &g) //创建图 { Add_vexs(g); Add_arcs(g); }
/*Floyd.cpp文件*/ #include "graph.h" #define FALSE 0 #define TRUE 1 typedef int DistancMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; //存放路径长度 typedef int PathMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM][MAX_VERTEX_NUM]; //存放路径,P[0][1][]表示顶点0到顶点1的路径,经过哪个点P[0][1][i]就是TRUE。 void Print_DistancMatrix(MGraph g,DistancMatrix &D) //打印距离矩阵 { int i; printf("\t\t距离矩阵为:\n"); printf("┏ "); //五个空格 for (i=0;i<g->vexnum;i++) { printf("%c ",g->vexs[i]); } printf("\n\n"); for (i=0;i<g->vexnum;i++) { printf("%c ",g->vexs[i]); for (int j=0;j<g->vexnum;j++) { if (D[i][j]>0&&D[i][j]<10) printf("%d ",D[i][j]); else if (D[i][j]>9&&D[i][j]<100) printf("%d ",D[i][j]); else if (D[i][j]>99&&D[i][j]<1000) printf("%d ",D[i][j]); else if (D[i][j]>999&&D[i][j]<10000) printf("%d ",D[i][j]); else if(D[i][j]==INFINITY) printf("∞ "); } printf("\n\n"); } printf("-----------------------------------------\n"); } void Print_PathMatrix(MGraph g,PathMatrix &P) { int i; printf("\t\t最短路径矩阵为:\n"); for (i=0;i<g->vexnum;i++) { printf("#######"); for (int vexcount=0;vexcount<g->vexnum;vexcount++) { printf("%c ",g->vexs[vexcount]); } printf("\n\n"); for (int j=0;j<g->vexnum;j++) { printf("%d-->%d: ",i+1,j+1); for (int k=0;k<g->vexnum;k++) { printf("%d ",P[i][j][k]); } printf("\n\n"); } printf("-----------------------------------------\n"); } } void ShortestPath_Folyd(MGraph g,PathMatrix &P,DistancMatrix &D) { //用Floyd算法求有向网G中各对顶点v和w之间的最短路径P[v][w]及其带权长 //度D[v][w],若p[v][w][u]为TRUE,则u是从v到w当前求的最短路径上的顶点 int u,v,w,i; for (v=0;v<g->vexnum;++v) //对各节点之间初始已知路径及距离 for (w=0;w<g->vexnum;++w) { D[v][w]=g->arcs[v][w].adj; for (u=0;u<g->vexnum;++u) P[v][w][u]=FALSE; if (D[v][w]<INFINITY) //从v到w有直接路径 { P[v][w][v]=TRUE; //起点 P[v][w][w]=TRUE; //终点 }//if } for (u=0;u<g->vexnum;++u) for (v=0;v<g->vexnum;++v) for (w=0;w<g->vexnum;++w) { if(u==v || v==w || w==u) continue; if (D[v][u]+D[u][w]<D[v][w]) //从v经u到w的一条路径更短 { D[v][w]=D[v][u]+D[u][w]; for (i=0;i<g->vexnum;++i) P[v][w][i]=P[v][u][i]||P[u][w][i]; }//if } }//ShortestPath_Floyd int main() { // freopen("in","r",stdin);//freopen("out","w",stdout); MGraph g; Init_graph(g); Create_mgraph(g); Print_mgraph(g); DistancMatrix D; PathMatrix P; ShortestPath_Folyd(g,P,D); Print_DistancMatrix(g,D); Print_PathMatrix(g,P); return 0; }
输入数据:
6
123456
10
5 1 2
7 1 4
4 2 3
8 3 1
9 3 6
5 4 3
6 4 6
5 5 4
3 6 1
1 6 5
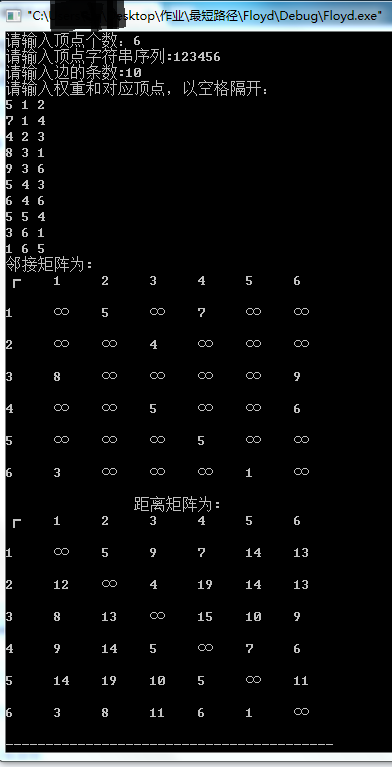
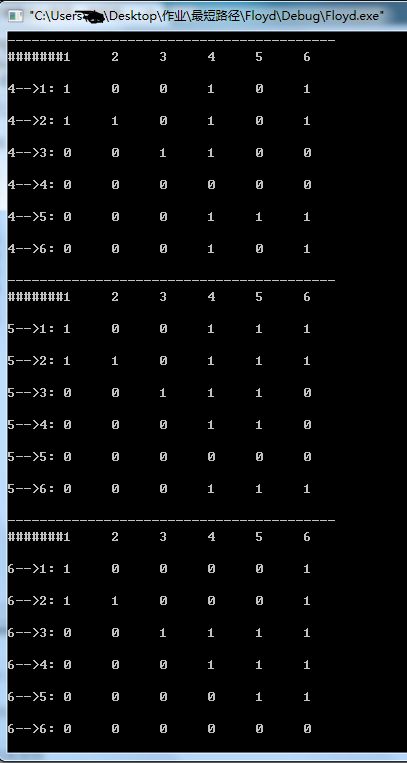
执行结果为: