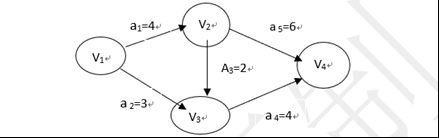
【数据结构课程设计】关键路径问题
1 问题描述与功能需求分析
1.1问题描述
1) 任务:设计一个程序求出完成整项工程至少需要多少时间以及整项工程中的关键活动。
2)基本要求:
(1)对一个描述工程的 AOE 网,应判断其是否能够顺利进行。
(2)若该工程能顺利进行,输出完成整项工程至少需要多少时间,以及每一个关键活动所依附的两个顶点、最早发生时间、最迟发生时间。
1.2 功能需求分析
1、用邻接表存储一张带权有向图。
2、对图进行拓扑排序,并进行事件的最早发生时间Ve[i]的计算。
3、根据排序结果,判断图中是否存在有向环。
4、根据逆拓扑序列,计算事件的最晚发生时间Vl[i]。
5、计算活动的最早、最晚发生时间,判断关键活动,找出关键路径。
2 概要设计
2.1 模块简介
依据程序的功能模块的划分,各模块定义如下:
(1);创建邻接表
int CreateAdjList(AdjList* G)用邻接表的算法来建立图,在邻接表的顶点增加一项数据为入度,用来保存每个结点的入度。通过遍历邻接表可以将每个元素的入度求出。
(2);拓扑排序
int TopoSort(AdjList G,SeqStack* T)在拓扑排序过程中,求顶点的 Ve[i],将得到的拓扑序列进栈。
(3);关键路径求解
voidCriticalPath(AdjList G, SeqStack* T)根据各顶点的ve和vl值,求每条弧s的最早开始时间e(s)和最迟开始时间l(s)。若某条弧满足条件e(s) = l(s),则为关键活动。
3 详细设计
3.1 数据结构
//弧结点结构
typedef struct ArcNode {
int adjvex; //该弧指向顶点的位置
struct ArcNode* nextarc; //指向下一条弧的指针
int activity; //弧表示的活动
int weight; //权值
}ArcNode;
//表头结点结构
typedef struct VertexNode {
VertexData data; //顶点数据
ArcNode* firstarc; //指向该顶点的第一条弧的指针
}VertexNode;
//邻接表结构
typedef struct {
VertexNode vertex[MAX_VERTEX_NUM];
int vexnum, arcnum; //图的顶点数和弧数
}AdjList;
3.2 算法分析与实现
# include
# include
# define MAX_VERTEX_NUM 20
# define TRUE 1
# define FALSE 0
/*AOE-网的邻接表表示法*/
typedef char VertexData;
//弧结点结构
typedef struct ArcNode {
int adjvex; //该弧指向顶点的位置
struct ArcNode* nextarc; //指向下一条弧的指针
int activity; //弧表示的活动
int weight; //权值
}ArcNode;
//表头结点结构
typedef struct VertexNode {
VertexData data; //顶点数据
ArcNode* firstarc; //指向该顶点的第一条弧的指针
}VertexNode;
//邻接表结构
typedef struct {
VertexNode vertex[MAX_VERTEX_NUM];
int vexnum, arcnum; //图的顶点数和弧数
}AdjList;
/*求顶点位置*/
int LocateVertex(AdjList* G, VertexData v) {
int k;
for (k = 0; k < G->vexnum; k++) {
if (G->vertex[k].data == v)
break;
}
return k;
}
/*创建AOE-网的邻接表*/
int CreateAdjList(AdjList* G) {
int i, j, k, activity, weight;
VertexData v1, v2;
ArcNode* p;
printf("输入图的顶点数和弧数:"); //输入图的顶点数和弧数
scanf("%d%d", &G->vexnum, &G->arcnum);
printf("输入图的顶点:");
for (i = 0; i < G->vexnum; i++) { //输入图的顶点,初始化顶点结点
scanf(" %c", &(G->vertex[i].data));
G->vertex[i].firstarc = NULL;
}
for (k = 0; k < G->arcnum; k++) {
printf("输入第%d条弧的两个顶点、弧表示的活动及权值:", k + 1);
scanf(" %c %c %d %d", &v1, &v2, &activity, &weight); //输入一条弧的两个顶点、弧表示的活动及权值
i = LocateVertex(G, v1);
j = LocateVertex(G, v2);
p = (ArcNode*)malloc(sizeof(ArcNode)); //申请新弧结点
p->activity = activity;
p->weight = weight;
p->adjvex = j;
p->nextarc = G->vertex[i].firstarc;
G->vertex[i].firstarc = p;
getchar();
}
}
/*顺序栈的存储结构*/
typedef struct {
int elem[MAX_VERTEX_NUM]; //用于存放栈中元素的一维数组
int top; //存放栈顶元素的下标,top为-1表示空栈
}SeqStack;
/*初始化顺序栈*/
void InitStack(SeqStack* S) {
S->top = -1;
}
/*判空*/
int IsEmpty(SeqStack* S) {
if (S->top == -1) //栈为空
return TRUE;
else
return FALSE;
}
/*顺序栈进栈*/
int Push(SeqStack* S, int x) {
if (S->top == MAX_VERTEX_NUM - 1) //栈已满
return FALSE;
S->top++;
S->elem[S->top] = x; //x进栈
return TRUE;
}
/*顺序栈出栈*/
int Pop(SeqStack* S) {
if (S->top == -1) //栈为空
return FALSE;
S->top--;
return TRUE;
}
int indegree[MAX_VERTEX_NUM]; //存放各顶点入度数
int ve[MAX_VERTEX_NUM]; //各顶点的最早发生时间
/*求各顶点入度算法*/
void FindID(AdjList G) {
int i;
ArcNode* p;
for (i = 0; i < G.vexnum; i++)
indegree[i] = 0;
for (i = 0; i < G.vexnum; i++) {
p = G.vertex[i].firstarc;
while (p != NULL) {
indegree[p->adjvex]++;
p = p->nextarc;
}
}
}
/*拓扑排序,求逆拓扑序列及事件最早发生时间ve(i)*/
int TopoSort(AdjList G, SeqStack* T) { //栈T用于生成逆拓扑序列
int i, k, count = 0;
SeqStack S; //栈S用于存放入度为0的顶点
ArcNode* p;
FindID(G); //求各顶点入度
InitStack(T); //初始化栈T
InitStack(&S); //初始化栈S
for (i = 0; i < G.vexnum; i++) {
if (indegree[i] == 0)
Push(&S, i); //将入度为0的顶点入栈S
}
for (i = 0; i < G.vexnum; i++)
ve[i] = 0; //初始化最早发生时间
while (!IsEmpty(&S)) {
i = S.elem[S.top];
Pop(&S);
count++;
Push(T, i); //按拓扑顺序进入栈T
p = G.vertex[i].firstarc;
while (p != NULL) {
k = p->adjvex;
indegree[k]--; //i号顶点的每个邻接点的入度减1
if (indegree[k] == 0)
Push(&S, k); //若入度减为0则入栈
if (ve[i] + p->weight > ve[k]) //按拓扑顺序计算事件最早发生时间
ve[k] = ve[i] + p->weight;
p = p->nextarc;
}
}
if (count < G.vexnum) {
printf("该图存在回路!\n");
return;
}
else
printf("\n事件最早发生时间为:"); //输出事件的最早发生时间
for (i = 0; i < G.vexnum; i++)
printf("%d ", ve[i]);
}
/*关键路径算法*/
void CriticalPath(AdjList G, SeqStack* T) {
ArcNode* p;
int i, j, k, dut, ei, li;
char tag;
int vl[MAX_VERTEX_NUM]; //每个顶点的最迟发生时间
TopoSort(G, T); //① 求事件最早发生时间和逆拓扑序列栈T
for (i = 0; i < G.vexnum; i++)
vl[i] = ve[G.vexnum - 1]; //将各事件的最晚发生时间初始化为汇点的最早发生时间
while (!IsEmpty(T)) { //② 按逆拓扑顺序求各顶点的最晚发生时间vl值
j = T->elem[T->top];
Pop(T);
p = G.vertex[j].firstarc;
while (p != NULL) {
k = p->adjvex;
dut = p->weight;
if (vl[k] - dut < vl[j])
vl[j] = vl[k] - dut;
p = p->nextarc;
}
}
printf("\n事件最晚发生时间为:"); //输出事件的最晚发生时间
for (i = 0; i < G.vexnum; i++)
printf("%d ", vl[i]);
printf("\n最少花费时间为:%d \n",ve[G.vexnum-1]);
printf("关键活动及对应的弧为:\n");
for (j = 0; j < G.vexnum; j++) { //③ 求各活动的最早开始时间ei和最晚开始时间li
p = G.vertex[j].firstarc;
while (p != NULL) {
k = p->adjvex;
dut = p->weight;
ei = ve[j];
li = vl[k] - dut;
if (ei == li) //④ 输出关键活动及对应的路径
printf("a%d v%c->v%c\n", p->activity, G.vertex[j].data, G.vertex[k].data);
p = p->nextarc;
}
}
}
int main() {
AdjList G;
SeqStack T;
CreateAdjList(&G);
CriticalPath(G, &T);
getchar();
return 0;
}
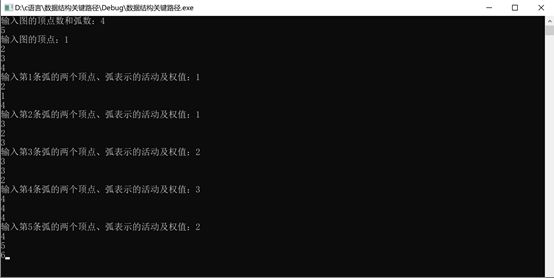
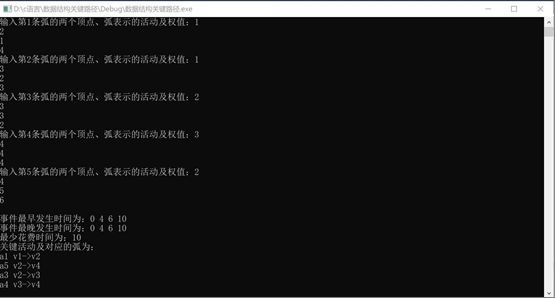
运行结果(以此题为例)
4 总结
在求关键路径的算法中,在求每一个事件的最早最迟发生时间,以及活动得到最早和最迟开始时,都要对所有顶点及每一个顶点边表中的边结点进行检查,因此求关键路径的时间复杂度为O(n+e)
~禁止转载~