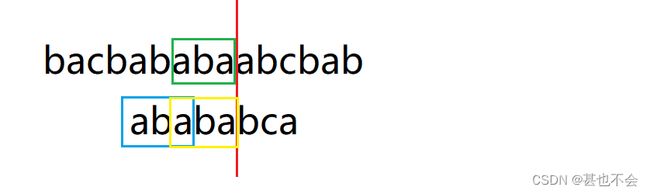y总算法基础课

第一章：基础算法

1.排序算法

1.1快排算法

//快排算法
    public static void quickSort(int[] arr,int start,int end){
        //递归终止条件:边界判断(只有一个点或者没有点的时候返回，一个点不用在排序)
        if(start>=end)return;
        
        //算法主体
        int stand=arr[start+end>>1];//标准数，即分界点，用来进行比较
        int left=start-1,right=end+1;
        while(left<right){
            //左指针移动
            do{
                left++;
            }while(arr[left]<stand);
            //右指针移动
            do{
                right--;
            }while(arr[right]>stand);
            
            //交换两个数
            if(left<right){
                int temp=arr[left];
                arr[left]=arr[right];
                arr[right]=temp;
            }
            
            
        }
        //递归处理左右两边
          quickSort(arr,start,right);
          quickSort(arr,right+1,end);
            
    }
    
}

1.2归并排序

 //归并排序
    public static void merge_sort(int[]arr,int left,int right){
        //递归终止条件:只有一个数时为有序，停止递归
        if(left>=right)return;
        //分界点，两个指针,临时数组接受排序后的数组
        int mid=left+right>>1;
        //递归处理左右两边
        //位置：处理上层，需要下一层是有序数组，故而如此
        merge_sort(arr,left,mid);
        merge_sort(arr,mid+1,right);
        //i:第一个数组头部，j：第二个数组头部，k：临时数组头部
        int i=left,j=mid+1,k=0;
        int[] temp=new int[right-left+1];
        //排序
        while(i<=mid && j<=right){//两个数组都未排完之时
        //两个数比较大小
        if(arr[i]<=arr[j]){
            //赋完值后两个指针向后移动一位
            temp[k++]=arr[i++];
        }else{
            temp[k++]=arr[j++];
        }
            
        }
        //对未完成的数组继续赋值
        while(i<=mid)temp[k++]=arr[i++];
        while(j<=right)temp[k++]=arr[j++];
        //将数组赋值回去:i指向数组起始位置，j指向temp起始位置
        for(int m=left,n=0;m<=right;i=m++,n++)arr[m]=temp[n];
        
    }

2.二分算法

2.1基本的二分

/*二分算法
*1.保持一个[]闭区间
*2.划分为3个区间  [left,mid-1],[mid,mid],[mid+1,right]
*3.根据不同的情况选择下一步搜索区间
*/

public int search(int[] nums, int target) {
        int left=0,right=nums.length-1;
        while(left<=right){//1.为什么是“<=”:因为维持的是一个[]闭区间，若left==right，则区                            //间中还有一个元素，需要再一次检索
            int mid=left+right>>1;
            if(nums[mid]==target){
                return mid;
            }else if(nums[mid]>target){
                right=mid-1;
            }else{
                left=mid+1;
            }
        }
        return -1;

    }

2.2左边界

//在一个非递减数组中寻找目标值的左侧边界，右侧边界可同理写出 
public static int left_bound(int[] nums,int target){
        int left=0,right=nums.length-1;
        while(left<=right){
            int mid=left+right>>1;
            if(nums[mid]==target){
                right=mid-1;//关键点：当找到目标值时，不急着返回，而是向左缩小区间，进一步向							//左探索
            }else if(nums[mid]>target){
                right=mid-1;
            }else{
                left=mid+1;
            }
        }
        //判断left是否越界，该值是否存在
        //1.while循环终止时：right=left-1；
        if(left>=nums.length || nums[left]!=target)return -1;
        return left;
    }

3.大数加减

• A,B:大整数

• a,b:较小的整数。

• A+B，A-B，A*a,A/a

• 大整数的存储：使用数组，由个位开始存

14567798：8存在res[0],以此向后。

3.1大数相加模板

• 大数相加方法

public static List<Integer> add(List<Integer> A,List<Integer> B){
        //存储结果的数组
        List<Integer> res=new ArrayList<>();
        //存储进位
        int t=0;
        for(int i=0;i<A.size() || i<B.size();i++){
            if(i<A.size())t=t+A.get(i);
            if(i<B.size())t=t+B.get(i);
            
            res.add(t%10);//本位数字
            t=t/10;//进位
            
        }
        //循环完之后，判断是否向更高进一位
        if(t!=0)res.add(1);
        return res;
        
    }

• 字符串转换方法

 List<Integer>  A=new ArrayList<>(a.length());
 for(int i=a.length()-1;i>=0;i--)A.add(a.charAt(i)-'0');

3.2大数相减

//高精度减法
/*1.比较两个数的大小
*    若A>B,则正常进行，否则，return sub（B,A）
* 2.  
*
*/
    public static List<Integer> sub(List<Integer> A,List<Integer> B){
     if(!cmp(A,B))return sub(B,A);
     //存储结果的列表
     List<Integer> res=new ArrayList<>();
     int t=0;
     for(int i=0;i<A.size();i++){
         t=A.get(i)-t;
         if(i<B.size())t=t-B.get(i);
         res.add((t+10)%10);
         
         if(t<0)t=1;
         else t=0;
         
     }
     //删除指定下标的值
     while(res.size()>1 && res.get(res.size()-1)==0)res.remove(res.size()-1);
     return res;
     
    }

• 大数比较

//大数比较：先比位数，再从高位逐一比较
public static boolean cmp(List<Integer> A,List<Integer> B){
        //2.1位数比较
        if(A.size()!=B.size())return A.size()>B.size();
        //2.2从高位比起
        for(int i=A.size()-1;i>=0;i--){
            if(A.get(i)!=B.get(i))return A.get(i)>B.get(i);
            }
            return true;
            
        }

3.3大数相乘

• 一个大数与一个小整数相乘
• 主要规则：将大整数A的每一位与b整体相乘

//大整数乘法
/*1.初始进位为0
 *2.A的每一位与b整体相乘
 *		答案对应位为  (Ai*b+t)%10
 *      进位更新为t/10
 */ 
public static List<Integer> mul(List<Integer> A,int b){
        List<Integer> res=new ArrayList<>();
        int t=0;
        for(int i=0;i<A.size() || t!=0;i++){//有进位或者存在乘数都要继续进行
         if(i<A.size())t=t+A.get(i)*b;
         res.add(t%10);
         t=t/10;
        }
        //如果b为0，则要清除前导0
        int n=res.size();
        while(res.size()>1){
            if(res.get(n-1)==0){
                res.remove(n-1);
                
            }else{
                break;
                
            } 
            n=res.size();
        }
        return res;
        
    }

3.4大数除法

//大数除法 
public static List<Integer> div(List<Integer> A,int b){
        List<Integer> res=new ArrayList<>();
        int t=0;
        for(int i=A.size()-1;i>=0;i--){
           t=t*10+A.get(i);
           res.add(t/b);
           t=t%b;
        }
        Collections.reverse(res);
        //去除前导0
        while(res.size()>1 && res.get(res.size()-1)==0)res.remove(res.size()-1);
        res.add(t);//最后一位记录余数
        return res;
    }

4.前缀和差分

4.1一维前缀和

• 数列前缀和
• 定义S[0]=0:更好的解决边界问题

/*一维数组的前缀和
*1.维护：s[i]=s[i-1]+a[i]
*2.[l,r]区间和：s[r]-s[l-1];
*3.前缀和下标从1开始，避免下标的转换
*4.s[0] = 0
*  s[1] = s[0]+a[1]
*  s[2] = s[1] + a[2]
*/

4.2二维前缀和

• 0行0列空出
• Sij 的计算：分行计算

//计算公式
S[i][j]=S[i-1][j]+S[i][j-1]-S[i-1][j-1]+a[i][j]

• （x1,y1）与(x2,y2)之间的所有数的和。

S[x2][y2]-S[x1-1][y2]-S[x2][y1-1]+S[x1-1][y1-1];

4.3差分数组

• 下标从1开始计算

• 前缀和的逆运算：即构造一个前缀和为已知数组A的数组b

• 作用：让指定区间 [l,r] 内所有的数加上C；

5.双指针算法

核心思想在于，利用数列某种单调性质，将降低算法复杂度

• 指向两个数列
• 指向同一个数列
  • 同向
  • 反向

第二章：数据结构

• 链表
• 栈与队列
• KMP

1.链表

1.1单链表

这里我们有用两个数组来模拟单链表的实现，两个数组通过下标关联起来

• e[i]:存储节点i的val值

• ne[i]:存储节点的指针

import java.util.*;
import java.io.*;
//只可向后遍历
class Main{
    public static int N=100010;
    //head:头节点下标
    //e[i]:节点的val
    //ne[i]:节点i的next
    public static int head=-1;
    public static int[] e=new int[N];
    public static int[] ne=new int[N];
    public static int idx=0;//存储当前已经用到的地址（指针）
    public static void main(String[] args)throws IOException{
        //1.将单链表初始化
        init();
        Scanner sc=new Scanner(System.in);
        int m=sc.nextInt();
        while(m-->0){
            //因为java中没有输入一个字符，所以用字符串转字符
            String s=sc.next();
            char op=s.charAt(0);
            if(op=='H'){
                int val=sc.nextInt();
                addHead(val);
            }else if(op=='D'){
                int k=sc.nextInt();
                if(k==0)head=ne[head];
                else delete(k-1);//第k个插入数，索引
            }else{
                int k=sc.nextInt();
                int val=sc.nextInt();
                insert(k-1,val);
            }
        }
        //输出
        for(int i = head;i != -1;i = ne[i] ){
            System.out.print(e[i] +  " ");
        }
        
    }
    //方法体
    //1.初始化
   public static void init(){
        head=-1;
        idx=0;
    }
    //2.插入
    public static void addHead(int val){
        e[idx]=val;//先将对应值进行存储
        ne[idx]=head;//新节点指向第一个节点
        head=idx;//head指向新节点
        idx++;//指向下一个使用的位置
    }
    //3.将val插入下标为k的节点后面
   public static void insert(int k,int val){
        e[idx]=val;
        ne[idx]=ne[k];
        ne[k]=idx;
        idx++;
    }
    //4.删除下标为k后面的点删除
    public static void delete(int k){
        ne[k]=ne[ne[k]];
    }
    
}

1.2双链表

我们依旧使用数组进行模拟

• e[i]:节点i的val
• l[i]:节点i的左指针
• r[i]:节点i的右指针
• idx：指向当前可用区间

1.3邻接表

实际上就是单链表

2.栈与队列

• 栈：先进后出
• 队列：先进先出

2.1栈的实现

• 栈的常见操作
  • Stack():构造方法
  • boolean isEmpty():判空操作
  • int size（）：返回栈中元素数量
  • void push（int x）:压入，
  • int pop():弹出
  • int peek（）：查看栈顶元素
• 栈的数组模拟实现

/*
*/
import java.util.*;
import java.io.*;
class Main{
    public static int N=100010;
    
    public static int[] st=new int[N];//数据存储
    public static int top=-1;//栈顶指针,指向栈顶元素
    public static int n;
   
    //压入
    public static void push(int val){
        st[++top]=val;
    }
    //弹出
    public static int pop(){
        return st[top--];
    }
    //判空
    public static boolean isEmpty(){
        return top<0;
    }
    //弹出
    public static int peek(){
        if(isEmpty()){
            System.out.println("栈为空");
            return -1;
        }else{
            return st[top];
        }
    }
    
}

 public static void main(String[] args)throws IOException{
        Scanner sc=new Scanner(System.in);
        int m=sc.nextInt();
        // System.out.println(m);
        while(m-->0){
            String s=sc.next();
            if(s.equals("push")){
                int val=sc.nextInt();
                push(val);
               
            }else if(s.equals("pop")){
                pop();
                
            }else if(s.equals("empty")){
                if(isEmpty()){
                    System.out.println("YES");
                }else{
                    System.out.println("NO");
                }
                
            }else{
                System.out.println(query());
                
            }
        }
        
    }

• 使用Deque

Deque<Integer> stack=new Deque<>();
//压入
void push()
//弹出
int   pop()
//判空
boolean isEmpty()
//栈中元素数量
int size()
//查看栈顶
int peek()

2.2单调栈

• 给定一个序列，求序列中每一个数左边最近的比他小的数，没有则返回-1；
• 示例

​ 3 4 2 7 5

ans：-1 3 -1 2 -1

//单调栈写法
int[] nextGreaterElement(int[] nums) {
    int n = nums.length;
    // 存放答案的数组
    int[] res = new int[n];
    Deque<Integer> s = new ArrayDeque<>(); 
    // 主体部分
    for (int i =0; i <n; i++) {
        // 判定个子高矮
        while (!s.isEmpty() && s.peek() <= nums[i]) {
            // 矮个起开，反正也被挡着了。。。
            s.pop();
        }
        //对应答案操作
        res[i] = s.isEmpty() ? -1 : s.peek();
       //将所有比自己小的元素弹出后，自己压入
        s.push(nums[i]);
    }
    return res;
}

2.3队列的实现

• 先进先出

/*1.队列常用方法
*Boolean isEmpty():判空
*int  size()：元素数量
*void offer(val):入队
*int poll():出队
*int  peek():出队
*/

• 数组模拟

import java.util.*;
import java.io.*;
class Main{
    //一个数组，两个指针，队尾入，对头出
    public static int N=100010;
    public static int[] q=new int[N];
    public static int tt=-1;//队尾
    public static int hh=0;//队头
    
    //插入
    public static void push(int val){
        q[++tt]=val;
    }
    //pop()
    public static int pop(){
        return q[hh++];
    }
    //判空
    public static boolean isEmpty(){
        return hh>tt;
    }
    //查询
    public static int query(){
        if(isEmpty()){
            System.out.println("队列为空");
            return -1;
        }else{
            return q[hh];
        }
    }
}

• 主方法

public static void main(String[] args)throws IOException{
        Scanner sc=new Scanner(System.in);
        int m=sc.nextInt();
        // System.out.println(m);
        while(m-->0){
            String s=sc.next();
            if(s.equals("push")){
                int val=sc.nextInt();
                push(val);
            }else if(s.equals("pop")){
                pop();
            }else if(s.equals("empty")){
                if(isEmpty()){
                    System.out.println("YES");
                }else{
                    System.out.println("NO");
                }
            }else{
                System.out.println(query());
            }
        }
        
    }

• 用链表实现

Queue<Integer> q=new LinkedList<>();
//入队
void offer(val)
//出队
int poll()
//判空
boolean isEmpty()
 //查看
 int peek()

2.4单调队列

• 求滑动窗口里的最大值，或最小值

3.KMP算法

3.1基本概念

KMP算法是一个优化后的字符匹配算法。优化的核心要点：在匹配失败是并不是将p向后移动一位进行匹配，二十向后移动多位（next数组决定）

• s[]:模式串，即比较长的字符串
• p[]:模板串，即比较短的字符串
• 部分匹配值：前缀后缀最长共有元素的长度
  • 前缀：不包含最后一个字符的所有以第一个字符开头的连续子串；
  • 后缀：不包含第一个字符的所有以最后一个字符结尾的连续子串
• next[i]:p[1,j]的部分匹配值；下标从1开始，存储每一个下标对应的部分匹配值,只与模板串有关

3.2next数组

• 手动求解

p	a	b	c	a	b
下标	1	2	3	4	5
next[]	0	0	0	1	2

next[1]:一个字母,前缀后缀皆为空，0

next[2]:前缀={a};后缀={b};0

next[3]:前缀={ab,a};后缀={bc,b};0

next[4]:前缀={abc,ab,a};后缀={bca,ca,a};1

next[5]:前缀={abca,abc,ab,a};后缀={bcab,cab,ab,a}:2

• 代码实现

 /**实质上是自己与自己的匹配
         * ne[]：存储一个字符串以每个位置为结尾的‘可匹配最长前后缀’的长度。
         * 构建ne[]数组：
         *              1,初始化ne[1] = 0,i从2开始。
         *              2,若匹配，s[i]=s[j+1]说明1~j+1是i的可匹配最长后缀,ne[i] = ++j;
         *              3,若不匹配，则从j的最长前缀位置+1的位置继续与i比较
         *              (因为i-1和j拥有相同的最长前后缀，我们拿j的前缀去对齐i-1的后缀),
         *              即令j = ne[j],继续比较j+1与i，若匹配转->>2
         *              4,若一直得不到匹配j最终会降到0，也就是i的‘可匹配最长前后缀’的长度
         *              要从零开始重新计算
         */
//定义一个全局变量用来存储next
public static int N=10010;//根据数值范围确定
public static int[] ne=new int[N];//next数组
  public static void next(char[] chs,int n){
          for(int i = 2,j = 0;i <= n ;i++) {
            while(j!=0&&chp[i]!=chp[j+1]) j = ne[j]; 
            if(chp[i]==chp[j+1]) j++;
            ne[i] = j;
        }
        
    }

3.3匹配过程

• 两个字符串的匹配过程
• 当失配时不是向后移动一位而是

 if(next[i]>1){
　　允许跳过的字符数量 = 匹配长度 - 部分匹配表[匹配长度];//适用next数组下标从1开始的情况
  }else　{
　　允许跳过的字符数量 = 部分匹配表[匹配长度];
　}

1.为什么要进行这样移动？

举个例子：

长串：s=bacbababaabcbab

短串：p=abababca

此时失配：黄框=绿框；蓝框=黄框；——》蓝框=绿框。所以可以进行这样的移动减少匹配次数

2.每次失配时移动的数量如何确定？

每次失配时我们需要移动至：红线前只剩next[部分匹配长度]，所以

移动数量（跳过字符串数量）=匹配长度 - next[匹配长度]

3.这样的过程会造成答案的丢失么？

这里我们选取的是前后缀共有的最长长度，所以移动数量就是最小的，所以不会有答案的丢失。

/**
         * 匹配两个字符串：
         *      1，从i=1的位置开始逐个匹配，利用ne[]数组减少比较次数
         *      2，若i与j+1的位置不匹配（已知1~j匹配i-j~i-1)，
         *      j跳回ne[j]继续比较(因为1~j匹配i-j~i-1,所以1~ne[j]也能匹配到i-ne[j]~i-1)
         *      3，若匹配则j++,直到j==n能确定匹配成功
         *      4，成功后依然j = ne[j],就是把这次成功当成失败，继续匹配下一个位置
         */
public static void match(char[] chp,int n,char[] chs,int m,BufferedWriter bw)throws IOException{
         for(int i = 1,j = 0; i <= m;i++) {
            while(j!=0&&chs[i]!=chp[j+1]) j = ne[j];
            if(chs[i]==chp[j+1]) j++;
            if(j==n) {
                j = ne[j];
                bw.write(i-n+" ");
            }
        }
        
    }

4.Trie树

• 用来高效的存储和查找字符串集合的数据结构

4.1存储与查找

1.存储方式

假设存储字符串集合{abcdef,abdef,aced,bcdf,bcff,cbaa,bcdc}

1. 现在根节点之下查找是否存在第一个字母

   2.若存在，在该节点之下重复1

​ 否则，创捷该字母1，然后在字母1下重复以上操作

• 存储abcd

1.读取第 i 个（1个）字母 a（对应数字0）

2.查看 son [0] [0] 是否存在（不存在则为0）

​ 不存在，在son[0] [0]存入 本字符的下一行（++idx）

3.令k=son[0] [0],（进入对应的下一行）。

4.重复以上操作

2.查找

• 查找acbd

1.读取第 i 个（1）字母 a(对应0)

2.查看 son[0] [0] (son[k] [u], u为字母对应的数字，K为当前节点位置，存储的值为下一节点行序号) 是否存在

​ 不存在返回0

​ 存在继续3

3.存在，令k=son[0] [0] ,重复以上操作

4.返回 cnt[k].

 //成员变量
static int N=200010;
static int idx=0;//指针，指向下一个字母存储的行序号(未存储过字母的行)
static int[][] son=new int[N][26];//最多存储26个字母（节点的宽度）
static int[] cnt=new int[N];


//方法体
//插入
public static void insert(String str){
    char[] ch=str.toCharArray();
    int k=0,i=0;//i指向ch数组
    //遍历ch数组
    while(i<ch.length){
        //读取当前字母后，i向后移动
        int u=ch[i++]-'a';
        if(son[k][u]==0){
            son[k][u]=++idx;
        }
        k=son[k][u];
        
    }
    //存储完一个单词后做标记
    cnt[k]++;
}
//查询
  static int query(String str){
    char[] ch=str.toCharArray();
    int i=0,k=0;
    while(i<ch.length){
        int u=ch[i++]-'a';
        if(son[k][u]==0)return 0;
        k=son[k][u];
    }
    return cnt[k];
    
}

5.并查集

• 合并集合
• 查询某一个元素是否在两个集合中

5.1合并集合

• 基本原理：使用树来表示集合。
  • 树根编号就是节点编号
  • 每个节点存储他的父节点，p[x]表示x的父节点

1.如何判断树根？

if(p[x]==x)

2.如何求x的集合编号？

while(p[x]!=x)x=p[x]

3.如何合并两个集合

px是x的集合编号，py是y的集合编号

p[x]=y:

6.堆

• 手写堆

1.insert():插入一个数

2.min():求集合最小值

3.deletemin():删除最小值

#间接实现

4.delete（）：删除任一元素

5.change（）：修改任一元素

• 小根堆：根<=左右儿子
• 堆的存储：使用一维数组进行存储
  • 1为根节点
  • 左儿子：2x
  • 右儿子：2x+1

6.1堆排序

• 基本思路：先把数据构造成一个小根堆，每次都输出堆顶元素

7.哈希表

• 存储结构
  • 开放寻址法
  • 拉链法
• 字符串哈希方式

7.1Hash函数

• -10^9 ~10^9 ——》 0<= h(x) <=10^5
• 冲突解决
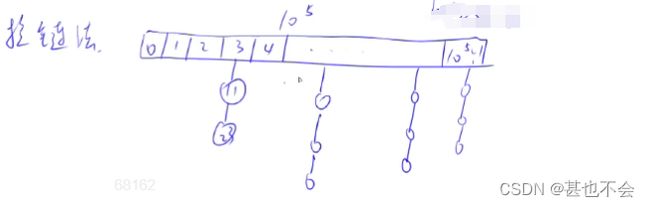
  • 拉链法
  • 开放寻址法
• 常见的hash：x mod 10^5：模尽量选去质数，距离2的整数次方近

拉链法

将冲突的值，并行存储在同一个hash值下