C++算法：排序之四（计数、基数、桶排序）

C++算法：排序

排序之一（插入、冒泡、快速排序）
排序之二（归并、希尔、选择排序）
排序之三（堆排序）
排序之四（计数、基数、桶排序）

---

---

本文续：C++算法：排序之三（堆排序）

---

三、非比较排序算法

非比较排序是一种不通过比较来决定元素间的相对次序的排序算法。它可以突破基于比较排序的时间下界，以线性时间运行，需要开辟额外的存储空间，因此也称为线性时间非比较类排序。常见的非比较排序算法包括桶排序、计数排序和基数排序。这些算法都不直接比较元素大小，而是通过计算每个元素有几个，应该在什么位置来实现的。由于整数也可以表达字符串（比如名字或日期）和特定格式的浮点数，所以非比较排序也不是只能使用于整数。

8、计数排序

计数排序是一种非比较型整数排序算法。它的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。它不是基于比较的排序算法，它不用循环的去一次次直接对比所有元素，所以时间复杂度较好。

还是用个例子说明一下，这个排序法用来对成绩之类的大小元素差很有限的，且重复元素很多的情况是非常好用的，比任何排序法都快。

一个简单的计数排序的例子：

• 假设我们有一个数组 [4, 3, 2, 1, 4, 3, 2, 4]，我们想要对它进行升序排序。
• 首先，找出数组中的最大值和最小值，这里是 4 和 1。
• 然后，创建一个计数数组，长度为最大值减最小值加1，即 [0, 0, 0, 0]。
• 接下来，遍历原数组，统计每个元素出现的次数。遍历完成后，计数数组变为 [1, 2, 2, 3]。
• 然后，从头开始遍历计数数组，将元素依次填充回原数组。最终得到排序后的数组 [1, 2, 2, 3, 3, 4, 4, 4]。
  

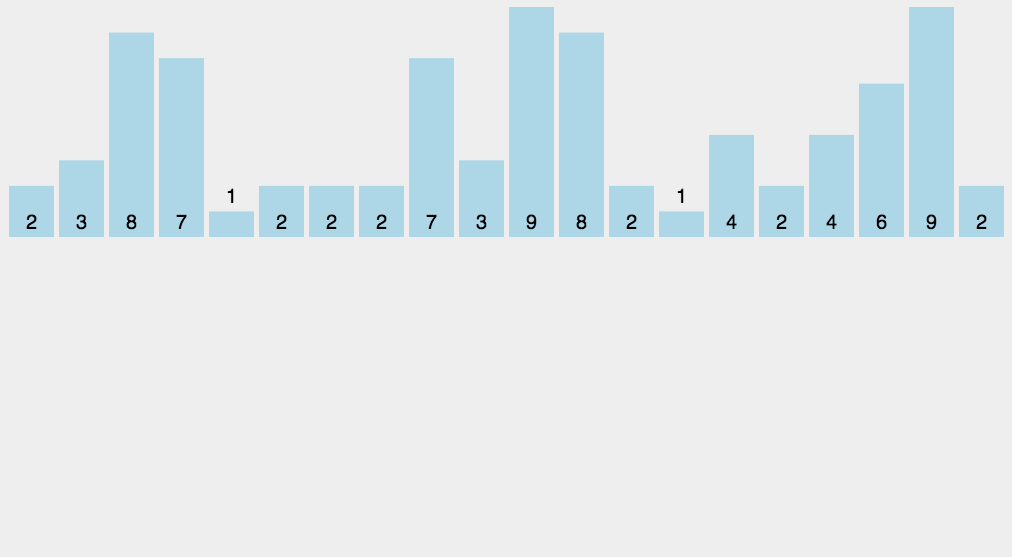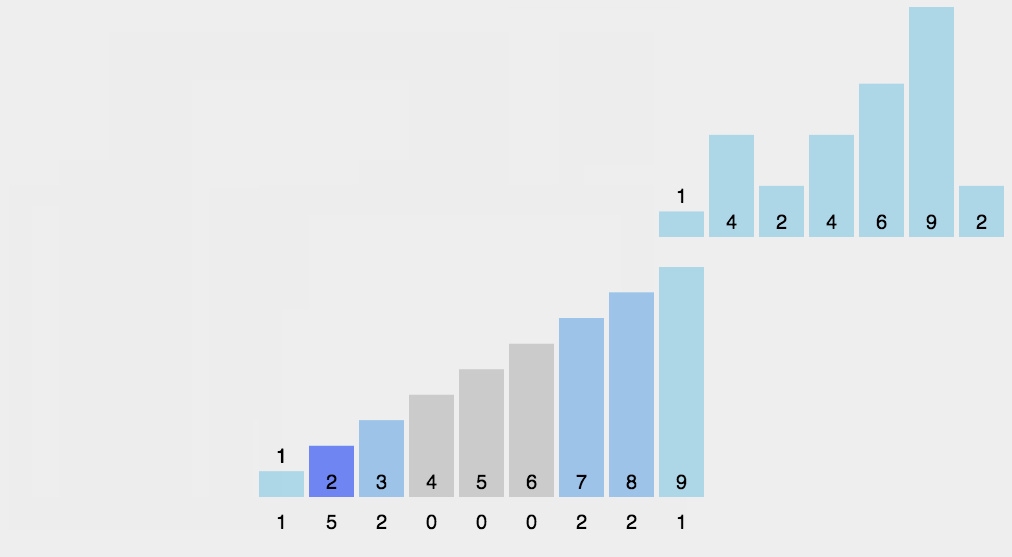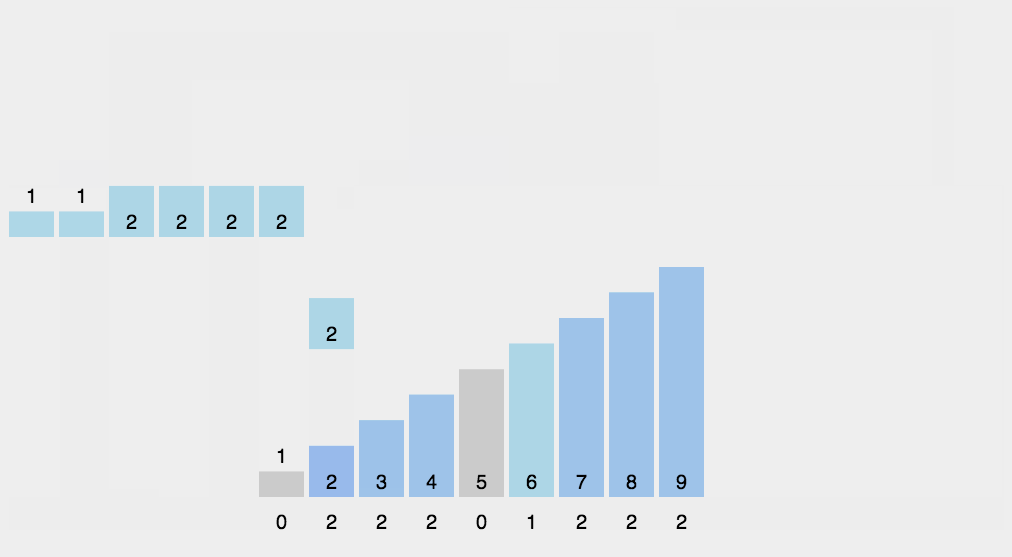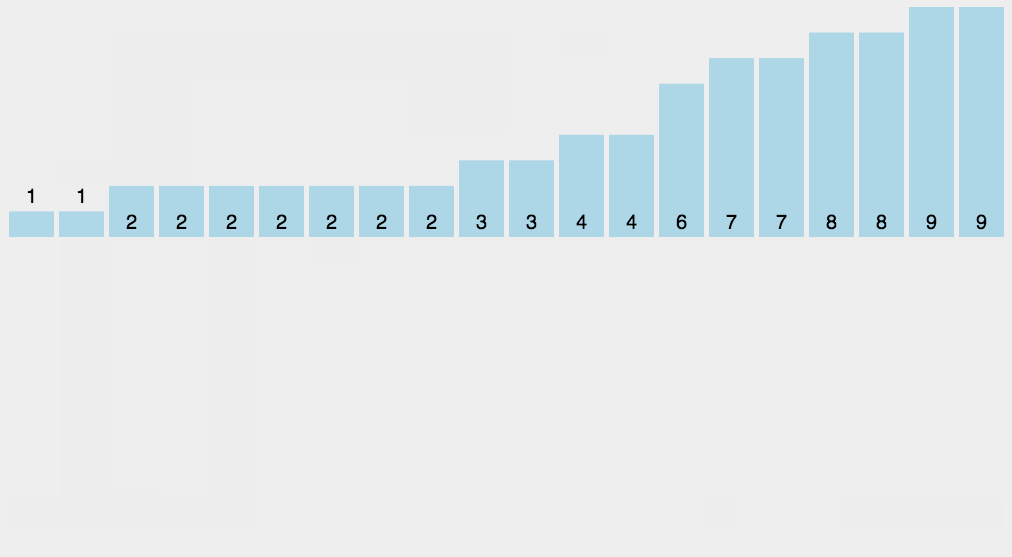
代码如下（与动图示例过程一致）：

#include 
#include 

using namespace std;

void count_sort(vector<int> &vec){  
    int len = vec.size();
    int idx = 0, mini, maxi;
    mini = vec[0];           //最小元素
    maxi = vec[0];           //最大元素
    for (int i=0; i<len; ++i){
        if (vec[i] > maxi){
            maxi = vec[i];
        } else if (vec[i] < mini){
            mini = vec[i];
        }
    }
    int k = maxi - mini + 1;     //放置每个元素数量的数组size
    int* arr = new int[k];       //生成数组
    for (int i=0; i<k; i++) arr[i] = 0;          //填充0
    for (int i=0; i<len; i++) arr[vec[i]-mini]++; //vec[i]-mini就是这个元素对应计数数组的下标
    for (int i=0; i<k; i++){   //把数组排序还原回去
        while (arr[i]-- >0){
            vec[idx++] = i + mini;  //idx是要排数组vec的下标，i+mini是vec[i]-mini的反向还原
        }
    }
    delete[] arr;
}

int main(){
    vector<int> vec = {2,3,8,7,1,2,2,2,7,3,9,8,2,1,4,2,4,6,9,2};
    count_sort(vec);
    for (auto it=vec.begin(); it!=vec.end(); it++){
        cout << *it << " ";
    }
    return 0;
}

这个代码逻辑清晰、简单易懂，就不再解释了，看看注释也就明白了。从这个计数排序的逻辑来看，它有一个很好的作用：将大数据转换为小数据来进行排序。明显小数据比较要比大数据快很多，很多要求对大量数据排序又要求低内存使用的情况可以考虑。内存不够它还可以分段。

9、基数排序

基数排序也是一种非比较型整数排序算法。它的原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。基数排序不是直接根据元素整体的大小进行元素比较，而是将原始列表元素分成多个部分，对每一部分按一定的规则进行排序，进而形成最终的有序列表。说人话就一句话：分个位、十位 … 单独比较。

代码如下（示例）：

include <iostream>
#include 
#include 

using namespace std;

void radix_sort(vector<int>& vec){
    const int base = 10;
    vector<int> temp(vec.size());
    int max_val = *max_element(vec.begin(), vec.end());
    for (int exp = 1; max_val / exp > 0; exp *= base){
        vector<int> count(base);
        for (int i = 0; i < vec.size(); i++){
            count[(vec[i] / exp) % base]++;
        }
        for (int i = 1; i < base; i++){
            count[i] += count[i - 1];
        }
        for (int i = vec.size() - 1; i >= 0; i--){
            temp[count[(vec[i] / exp) % base] - 1] = vec[i];
            count[(vec[i] / exp) % base]--;
        }
        vec = temp;
    }
}

int main(){
    vector<int> vec = {3,44,38,5,47,15,36,26,27,2,46,4,19,50,48};
    radix_sort(vec);
    for (auto it=vec.begin(); it!=vec.end(); it++){
        cout << *it << " ";
    }
    return 0;
}

在这个例子中，我们使用了LSD（Least significant digital）的基数排序方式，即从最低位开始进行排序。

首先，我们定义了一个常量base，表示十进制。

然后，我们定义了一个临时向量temp，用于存储排序过程中的中间结果。

max_element函数用来找到向量中的最大值，赋值给变量max_val。

接下来是一个外层循环，它从最低位开始，依次对每一位进行排序。循环变量exp表示当前正在处理的位数。循环条件是max_val / exp > 0，表示只要还有更高位就继续循环。

在外层循环内部，我们首先定义了一个计数器向量count，用于存储每个桶中元素的个数。然后遍历输入向量中的每个元素，并根据当前位数更新计数器向量。

接着，我们对计数器向量进行前缀和处理，使得count[i]表示小于等于i的元素个数。

然后再次遍历输入向量中的每个元素，并根据计数器向量将它们放入临时向量中正确的位置上。

最后，将临时向量复制回输入向量，并更新循环变量exp。

外层循环结束后，输入向量就已经排好序了。这个排序用处不是太大，代码不长逻辑却比较绕。只适用于整数，字符串可以表示为整数。时间复杂度为O(kn)，k是整数最大位数。空间复杂度和时间复杂度一样。

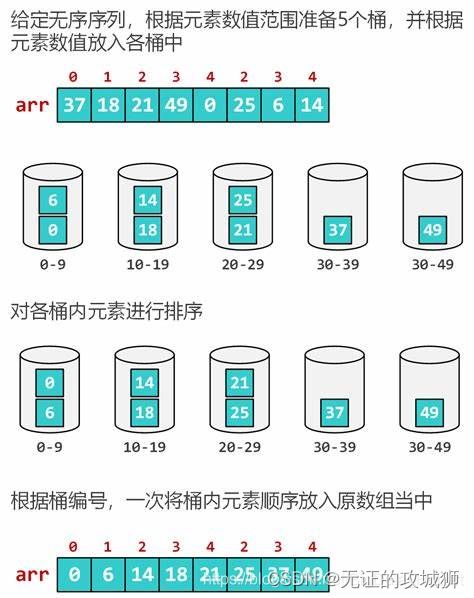
10、桶排序

桶排序也是一种非比较排序算法。它不受到O(N*logN)下限的影响。桶排序的思想近乎彻底的分治思想。桶排序假设待排序的一组数均匀独立的分布在一个范围中，并将这一范围划分成几个子范围（桶）。它可以突破基于比较排序的时间下界，以线性时间运行，因此也称为线性时间非比较类排序。没找到合适的动图，不过下图也很能说明排序原理了：

代码如下（示例）：

#include 
#include 
#include 
#include 

using namespace std;

void insert_sort(vector<int>& arr){
    for (int i = 1; i < arr.size(); i++){
        int key = arr[i];
        int j = i - 1;
        while (j >= 0 && arr[j] > key) {
            arr[j + 1] = arr[j];
            j--;
        }
        arr[j + 1] = key;
    }
}

void bucket_sort(vector<int>& arr){
    int n = arr.size();
    int max_val = *max_element(arr.begin(), arr.end());
    int min_val = *min_element(arr.begin(), arr.end());
    int range = max_val - min_val + 1;
    int bucket_size = ceil(range / n);
    vector<vector<int>> buckets(n+1);
    for (int i = 0; i < n; i++) {
        int index = (arr[i] - min_val) / bucket_size;
        buckets[index].push_back(arr[i]);
    }
    for (int i = 0; i < n; i++){
        insert_sort(buckets[i]);
    }
    int index = 0;
    for (int i = 0; i < n+1; i++){
        for (int j = 0; j < buckets[i].size(); j++){
            arr[index++] = buckets[i][j];
        }
    }
}

int main(){
    vector<int> vec = {37,18,21,49,0,25,6,14};
    bucket_sort(vec);
    for (auto it=vec.begin(); it!=vec.end(); it++){
        cout << *it << " ";
    }
    return 0;
}

代码中，bucket_sort 函数首先计算出待排序数组中的最大值和最小值，以及它们之间的范围。然后根据数组的大小和范围计算出每个桶的大小和桶的数量。接下来，遍历数组中的每个元素，根据元素的值计算出它应该放入哪个桶中，并将其放入对应的桶中。然后对每个桶中的数据进行插入排序。最后，将所有桶中的数据依次取出并放回原数组中，即可得到一个有序序列。

桶排序主要适用于输入数据均匀分布在一个范围内的情况。它是计数排序的扩展版本，计数排序可以看成每个桶只存储相同元素，而桶排序每个桶存储一定范围的元素。通过映射函数将待排序数组中的元素映射到各个对应的桶中，然后对每个桶中的元素进行排序，最后将非空桶中的元素逐个放入原序列中。

---

总结

这些算法各有优缺点，适用于不同的场景。一般来说，冒泡排序、选择排序和插入排序适用于小规模的数据，因为它们的时间复杂度较高，但是空间复杂度较低，且易于实现。

希尔排序是对插入排序的改进，通过增加间隔来减少比较次数，适用于中等规模的数据。

归并排序和快速排序是分治法的典型应用，它们可以将大规模的数据分成小块进行排序，然后再合并，适用于大规模的数据，但是需要额外的空间。

堆排序是利用堆这种数据结构来实现的，它可以在不使用额外空间的情况下，对大规模的数据进行排序，但是比较次数较多，且不稳定。

计数排序、桶排序和基数排序是非比较型的算法，它们可以在线性时间内对特定范围或位数的数据进行排序，但是需要较大的空间，并且对数据的分布有一定的要求。

实际应用中，一般情况下，即输入数据是随机的，快速、归并、希尔、堆排序的效果最好。其中快速排序最快，堆排序最省空间。如果数据是基本有序的，插入和冒泡排序效果最好O(n)。其它排序法也都有一定的适用场景，要根据数据分布、类型、规模等综合考虑采用哪种排序算法。

到此排序部分就全部写完了，基本能保证测试数据能跑通，因为很多排序算法有不同实现方法，笔者基本上按照动图中演示的过程写的代码（快排的动图是取中间元素划界，但笔者的实现是最后元素划界，基数排序也不能保证–这就不是我写的）。写成这一系列文章也不容易，万多字，仅代码也不太可能一天写完并测试，所以分了几天才完成。

原创文章，未经许可，严禁转载