多目标优化NSGA-II的实现和测试（MATLAB实现）
NSGA-II系列文章目录
第一章 基于NSGA-II算法的研究和改进
第二章 进化算法框架的介绍及Matlab实现（遗传算法）
第三章 NSGA-II的算法介绍
第四章 传统的NSGA-II的实现和测试（MATLAB实现）
第五章 NSGA-II的算法的改进及测试结果
目录
NSGA-II系列文章目录
前言
一、简单的框架描述
二、各函数的实现代码及解释
1.主函数
2.确定问题变量维度及界限
3.种群初始化
4.种群计算函数
三、测试结果：
1.测试函数
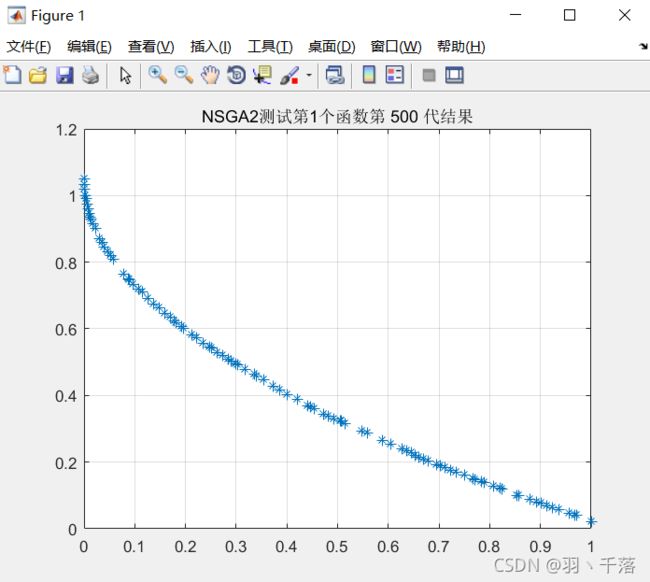
2.测试结果
总结
前言
NSAG-II框架的MATALB实现。测试函数为ZDT1--6。
种群的数据结构：[dimension+target_evaluate+rank+distance] 即为：popsize*(变量的维度+目标评估数量+支配排序的个体等级+拥挤距离）的矩阵
函数：由于代码过多，这里就只放几个函数的代码，整个代码文件需要的可以查看以下链接
多目标优化NSGA-II的实现（MATLAB完整代码）_羽丶千落的博客-CSDN博客
https://blog.csdn.net/weixin_44034444/article/details/122292991
- function [pop,i,GD,SP] = nsga2_main(x) %主函数
- function [bounds,dimension] = get_variable_bounds(x) %确定测试函数的变量及范围
- function pop = init_pop(pop_size,dimension,bounds,x) %初始化种群
- function pop = sort_pop(pop_eva,target,dimension) %非支配排序及计算拥挤距离
- function parent_pop = select_parent(pop,parent_size,compare_size) %父代个体的选择
- function child_pop = myga(parent_pop,dimension,bounds,x) %GA算法中的杂交和变异
- function pop = combined_pop(pop,child_pop,target,dimension) %合并父代和子代个体
- function pop = select_pop(pop,target,dimension,pop_size) %选择新一代种群
- function evaluate = calculate_pop(pop,x) %计算种群
- function sp= calculate_sp(pop) %计算SP
- function gd= calculate_gd(pop) %计算GD
一、简单的框架描述
这是在开始写代码之前自己初始定的框架，了解自己需要完成那些内容，需要定义那些参数，定义那些函数。这个不是很完善，是一个初始化版本，后续也没有维护这个，这个只作为一个参考
主函数：
参数设置：
种群大小pop_size
迭代次数iterations
种群取值范围bounds
目标数量：target
目标维度：dimension
种群初始化
初始非支配排序
for 1 ：迭代次数
选择父代个体P_pop
遗传算法产生子代个体C_pop
原始种群Y_pop和子代C_pop合并为Pop
对Pop进行非支配排序
选择新一代种群Y_pop
end
其他函数：
种群初始化函数 pop = initialize(pop_size,bounds,dimension)
初始化种群，计算种群适应值。
种群适应值计算函数 evaluate = calculate_pop(pop_d)
计算种群适应值。
选择父代个体函数（锦标赛选择）parent_pop = select_parent(pop,parent_size,select_size)
for i =1:parent_size
随机选择select_size个体，
选择等级最高的一个
若有等级一样高，则根据拥挤距离选择
end
遗传算法函数 pop_child = (parent_pop)
设定杂交概率和变异概率
合并函数 pop = combined_pop(pop_child,pop)
可以不取最后两列，等级和距离
非支配排序函数
计算得到个体等级
计算得到拥挤距离
选择新一代种群函数
先选择等级最高的
若等级最高的超出种群数量，则根据距离选择
不满就下一等级
二、各函数的实现代码及解释
1.主函数
代码如下（示例）：
function [pop,i,GD,SP] = nsga2_main(x)
%%测试主函数
%参数设置
pop_size = 100;
iterations = 500;%迭代次数
target = 2;
[bounds,dimension] = get_variable_bounds(x);
%种群初始化
pop = init_pop(pop_size,dimension,bounds,x);
%种群排序
pop = sort_pop(pop,target,dimension);
%锦标赛参数设置
parent_size = pop_size/2;
select_size = 2;
% 初始化函数返回数据
GD = zeros(1,iterations);
SP = zeros(1,iterations);
allpop = zeros(iterations,pop_size,dimension+4);
warning off all
%迭代循环
for i = 1:iterations
%选择父代
parent_pop = select_parent(pop,parent_size,select_size);
%进行遗传算法，杂交变异
child_pop = myga(parent_pop,dimension,bounds,x);
%子代和父代进行合并
pop = combined_pop(pop,child_pop,target,dimension);
%对合并种群进行非支配排序
pop = sort_pop(pop,target,dimension);
%选择新一代种群
pop = select_pop(pop,target,dimension,pop_size);
%画出种群迭代的过程
plot(pop(:,dimension+1),pop(:,dimension+2),'*')
grid on
title(['NSGA2测试第',num2str(x),'个函数第 ',num2str(i),' 代结果'])
pause(0.1)
end
end
2.确定问题变量维度及界限
代码如下（示例）：使用switch方法
function [bounds,dimension] = get_variable_bounds(x)
switch x
case 1
dimension = 30;
bounds = [ones(dimension,1)*0,ones(dimension,1)*1];
case 2
dimension = 30;
bounds = [ones(dimension,1)*0,ones(dimension,1)*1];
case 3
dimension = 30;
bounds = [ones(dimension,1)*0,ones(dimension,1)*1];
case 4
dimension = 10;
bounds = [zeros(1,1),ones(1,1);ones(9,1).*-5,ones(9,1).*5];
case 5
dimension = 10;
bounds = [ones(dimension,1)*0,ones(dimension,1)*1];
case 6
dimension = 20;
bounds = [ones(dimension,1)*-4,ones(dimension,1)*4];
end3.种群初始化
种群初始化采用随机初始化的方法，代码如下（示例）：
function pop = init_pop(pop_size,dimension,bounds,x)
p = rand(pop_size,dimension);%生成popsize*dimension的0-1矩阵
%生成定义域范围内种群
for i = 1:dimension
p(:,i) = bounds(i,1)+p(:,i)*(bounds(i,2)-bounds(i,1));
end
%计算种群的适应值
evaluate = calculate_pop(p,x);
pop = [p,evaluate];4.种群计算函数
代码如下（示例）：
function evaluate = calculate_pop(pop,x)
%测试函数
[~,dim] = size(pop);
switch x
case 1 %ZDT1
fx1 = pop(:,1);
gx = 1+sum(pop(:,2:end),2).*(9/(dim-1));
hx = 1-sqrt(fx1./gx);
fx2 = gx.*hx;
evaluate = [fx1,fx2];
case 2 %ZDT2
fx1 = pop(:,1);
gx = 1+sum(pop(:,2:end),2).*(9/(dim-1));
hx = 1-(fx1./gx).^2;
fx2 = gx.*hx;
evaluate = [fx1,fx2];
case 3 %ZDT3
fx1 = pop(:,1);
gx = 1+sum(pop(:,2:end),2).*(9/(dim-1));
hx = 1-sqrt(fx1./gx)-(fx1./gx).*sin(10*pi.*fx1);
fx2 = gx.*hx;
evaluate = [fx1,fx2];
case 4 %ZDT4
fx1 = pop(:,1);
gx = 91+sum((pop(:,2:dim).^2-10.*cos(4*pi.*pop(:,2:dim))),2);
hx = 1-sqrt(fx1./gx);
fx2 = gx.*hx;
evaluate = [fx1,fx2];
case 5
x1 = pop(:,1);
fx1 = 1-exp(-4.*x1).*(sin(6*pi.*x1)).^6;
s = sum(pop(:,2:end),2);
gx = 1+9/(dim-1).*s;
hx = 1-(fx1./gx).^2;
fx2 = gx.*hx;
evaluate = [fx1,fx2];
case 6
n = -sum((pop-1/sqrt(dim)).^2,2);
m = -sum((pop+1/sqrt(dim)).^2,2);
fx1 = 1-exp(n);
fx2 = 1-exp(m);
evaluate = [fx1,fx2];
end
三、测试结果：
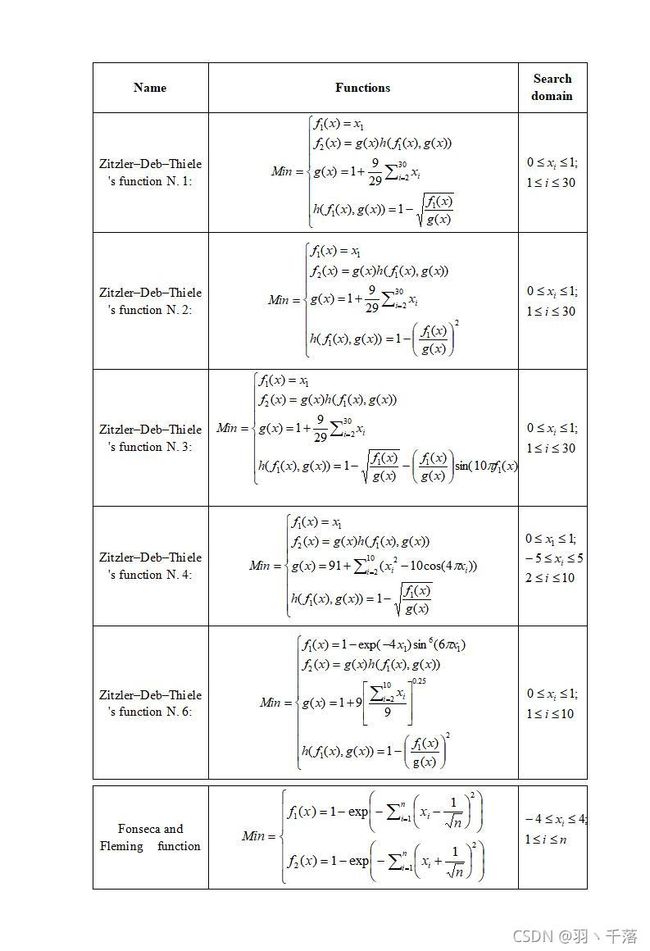
1.测试函数
2.测试结果
ZDT1： ZDT2：
ZDT3： ZDT4：
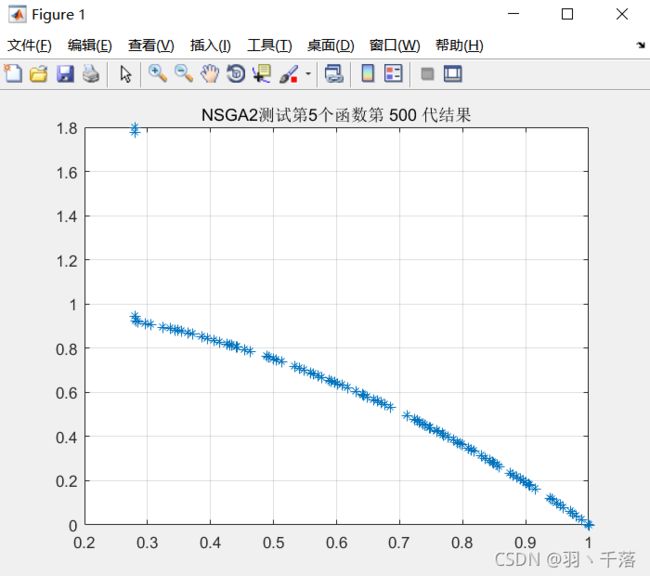
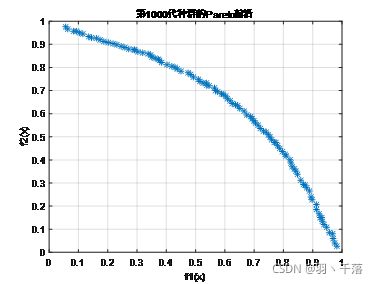
ZDT5： Fonseca and Fleming function
改变遗传策略之后之后Fonseca and Fleming function的测试结果：此图是以前测试的结果，因为是另一种遗传策略，不想再敲代码运行，就直接复制之前的图片了。
总结
第4个函数测试的结果也是一个很差的结果，在知网上查看相关的文献，很多论文都并没有把ZDT4作为测试函数，当然如果改进策略，还是可以得到一个好的结果的；第6个测试函数，如果不改进策略，依旧采用多项式杂交和多项式变异的方法是无法得到一个结果，只有改变遗传算法的策略，才能得到结果；其他测试函数，基本上nsga2是可以求解出来，但结果也是特别的完美，与真实的前言还是有一点点的差距的。可以查看我系列文章的第一章的内容，可以看到改进后的算法，不管是在结果，还是在效率上都远比未改进的好。
第4个函数进行非支配排序和计算拥挤距离。这一块的代码可以参考MathWork中代码。这里也有nsga2的整个实现方法，但计算效果并不理想，计算时间长，效果也不好。所以只借鉴的这一部分的代码，在杂交和变异也一样是用了多项式杂交和变异，但并没有复用代码，而是重写了。MathWork中的nsga2代码的链接：https://ww2.mathworks.cn/matlabcentral/fileexchange/10429-nsga-ii-a-multi-objective-optimization-algorithm?s_tid=srchtitle_NSGA_1https://ww2.mathworks.cn/matlabcentral/fileexchange/10429-nsga-ii-a-multi-objective-optimization-algorithm?s_tid=srchtitle_NSGA_1
https://ww2.mathworks.cn/matlabcentral/fileexchange/10429-nsga-ii-a-multi-objective-optimization-algorithm?s_tid=srchtitle_NSGA_1