LeetCode刷题（ACM模式）-01数组

参考引用：代码随想录

• 注：每道 LeetCode 题目都使用 ACM 代码模式，可直接在本地运行，蓝色字体为题目超链接

0. 数组理论基础

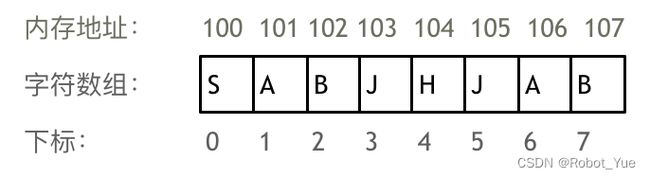
• 数组（array）是存放在连续内存空间上的相同类型数据的集合，是一种复合数据类型，它是有序数据的集合，在存储空间中也是按顺序存储。数组中的每个元素具有相同的数据类型，可以方便的通过下标索引的方式访问到对应的数据。根据数组的维度，可以将其分为一维数组、二维数组和多维数组等。举一个字符数组的例子，如图所示
  • 数组下标都是从 0 开始的
  • 数组内存空间的地址是连续的
  • 数值数组元素的默认值为 0，而引用元素的默认值为 null
  • 数组元素可以是任何类型，包括数组类型

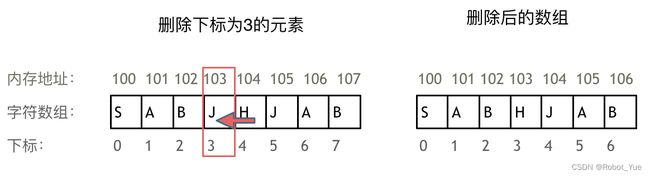
• 正是因为数组的在内存空间的地址是连续的，所以在删除或者增添元素的时候，就难免要移动其他元素的地址。例如删除下标为 3 的元素，需要对下标为 3 的元素后面的所有元素都要做移动操作，如图所示

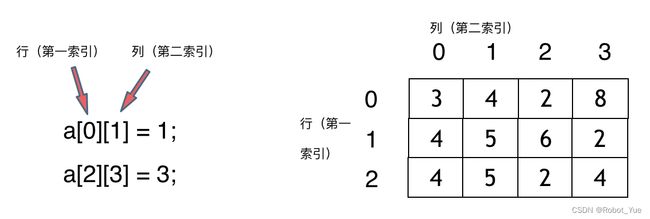
• 要注意 vector 和 array 的区别，vector 的底层实现是 array，严格来讲 vector 是容器，不是数组。数组的元素是不能删的，只能覆盖，平时删除操作也是依次用后一位覆盖，因为存储空间申请且初始化后就固定了，如下图二维数组所示。此外，在 C++ 中二维数组也是连续分布的

1. 二分查找

704. 二分查找
给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1

• 示例 1
  输入: nums = [-1,0,3,5,9,12]，target = 9
  输出: 4
  解释: 9 出现在 nums 中并且下标为 4
• 示例 2
  输入: nums = [-1,0,3,5,9,12]，target = 2
  输出: -1
  解释: 2 不存在 nums 中因此返回 -1
• 提示
  你可以假设 nums 中的所有元素是不重复的
  n 将在 [1, 10000] 之间
  nums 的每个元素都将在 [-9999, 9999] 之间

1.1 解题思路

• 使用二分法的前提条件

  • 数组为有序数组
  • 数组中无重复元素

• 二分法核心思想

  • 在二分查找的过程中，保持不变量，即：在 while 寻找每一次边界的处理都要坚持根据区间的定义来操作，这就是循环不变量规则
  • 区间的定义一般为两种，左闭右闭即 [left, right]，或者左闭右开即 [left, right)

1.2 二分法之左闭右闭

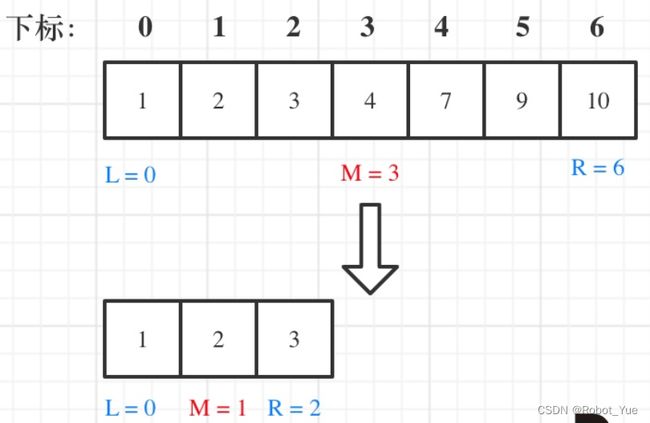
• 例如在数组：1,2,3,4,7,9,10 中查找元素 2，如图所示

// 时间复杂度：O(log n)
// 空间复杂度：O(1)
#include 
#include 

class Solution {
public:
    int search(std::vector<int> &nums, int target) {
        int left = 0;
        int right = nums.size() - 1; // 定义target在左闭右闭的区间里，[left, right]
        while (left <= right) { // 当left==right，区间[left, right]依然有效，所以用 <=
            int middle = left + ((right - left) / 2); // 防止溢出 等同于(left + right)/2
            if (nums[middle] > target) {
                right = middle - 1; // target 在左区间，所以[left, middle - 1]
            } else if (nums[middle] < target) {
                left = middle + 1; // target 在右区间，所以[middle + 1, right]
            } else { // nums[middle] == target
                return middle; // 数组中找到目标值，直接返回下标
            }
        }
        // 未找到目标值
        return -1;
    }
};

int main(int argc, char *argv[]) {
    std::vector<int> nums{ 1, 2, 3, 4, 7, 9, 10 };
    int target = 2;

    Solution solution;
    int result = solution.search(nums, target);

    std::cout << result << std::endl;
    return 0;
}

1.3 二分法之左闭右开

// 时间复杂度：O(log n)
// 空间复杂度：O(1)
#include 
#include 

class Solution {
public:
    int search(std::vector<int> &nums, int target) {
        int left = 0;
        int right = nums.size(); // 定义target在左闭右开的区间里，即：[left, right)
        while (left < right) { // 因为left == right的时候，在[left, right)是无效的空间，所以使用 <
            int middle = left + (right - left) / 2;
            if (nums[middle] > target) {
                right = middle;
            } else if (nums[middle] < target) {
                left = middle + 1;
            } else {
                return middle;
            }
        }
        return -1;
    }
};

int main(int argc, char *argv[]) {
    std::vector<int> nums{ 1, 2, 3, 4, 7, 9, 10 };
    int target = 2;

    Solution solution;
    int result = solution.search(nums, target);

    std::cout << result << std::endl;
    return 0;
}

2. 移除元素

27. 移除元素
给你一个数组 nums 和一个值 val，你需要原地移除所有数值等于 val 的元素，并返回移除后数组的新长度。不要使用额外的数组空间，你必须仅使用 $O(1)$ 额外空间并原地修改输入数组

• 示例 1
  给定 nums = [3,2,2,3], val = 3, 函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2
• 示例 2
  给定 nums = [0,1,2,2,3,0,4,2], val = 2, 函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4
• 提示
  元素的顺序可以改变
  你不需要考虑数组中超出新长度后面的元素
  数组的元素在内存地址中是连续的，不能单独删除数组中的某个元素，只能覆盖
  数组在内存中是连续的地址空间，不能释放单一元素，如果要释放，就是全释放（程序运行结束，回收内存栈空间）

2.1 暴力解法

• 两层 for 循环，第一个 for 循环遍历数组元素 ，第二个 for 循环更新数组
  

// 时间复杂度：O(n^2)
// 空间复杂度：O(1)
#include 
#include 

class Solution {
public:
    int removeElement(std::vector<int> &nums, int val) {
        int size = nums.size();
        for (int i = 0; i < size; ++i) {
            if (nums[i] == val) {
                // 发现需要移除的元素，就将数组集体向前移动一位
                for (int j = i + 1; j < size; ++j) {
                    nums[j - 1] = nums[j];
                }
                // 因为下标 i 以后的数值都向前移动了一位，所以如果不对 i 进行自减操作
                // 那么下次循环时会漏掉移动后的当前位置（即原来的下标 i+1）
                // 从而导致这个位置上的元素没有被处理到
                --i;
                --size; // 此时数组的大小 -1
            }
        }
        return size;
    }
};

int main(int argc, char *argv[]) {
    std::vector<int> nums{ 0, 1, 2, 2, 3, 0, 4, 2 };

    Solution solution;
    int result = solution.removeElement(nums, 2);

    std::cout << result << std::endl;
    return 0;
}

2.2 双指针法

• 双指针法（快慢指针法）：通过一个快指针和慢指针在一个 for 循环下完成两个 for 循环的工作
• 定义快慢指针
  • 快指针：寻找新数组的元素，新数组就是不含有目标元素的数组
  • 慢指针：指向更新的新数组下标的位置
    

// 时间复杂度：O(n)
// 空间复杂度：O(1)
#include 
#include 

class Solution {
public:
    int removeElement(std::vector<int> &nums, int val) {
        int slowIndex = 0;
        for (int fastIndex = 0; fastIndex < nums.size(); ++fastIndex) {
            if (val != nums[fastIndex]) {
                nums[slowIndex] = nums[fastIndex];
                ++slowIndex;
            }
        }
        return slowIndex;
    }
};

int main(int argc, char *argv[]) {
    std::vector<int> nums{ 0, 1, 2, 2, 3, 0, 4, 2 };

    Solution solution;
    int result = solution.removeElement(nums, 2);

    std::cout << result << std::endl;
    return 0;
}

3. 有序数组的平方

977. 有序数组的平方
给你一个按非递减顺序排序的整数数组 nums，返回每个数字的平方组成的新数组，要求也按非递减顺序排序

• 示例 1
  输入：nums = [-4,-1,0,3,10] 输出：[0,1,9,16,100] 解释：平方后，数组变为 [16,1,0,9,100]，排序后，数组变为 [0,1,9,16,100]
• 示例 2
  输入：nums = [-7,-3,2,3,11] 输出：[4,9,9,49,121]

3.1 暴力解法

• 每个数平方之后，排个序

// 时间复杂度：O(n + nlogn)
#include 
#include 
#include 

class Solution {
public:
    std::vector<int> sortedSquares(std::vector<int> &A) {
        for (int i = 0; i < A.size(); ++i) {
            A[i] *= A[i];
        }
        sort(A.begin(), A.end()); // 快速排序
        return A;
    }
};

int main(int argc, char *argv[]) {
    std::vector<int> A{ -7, -3, 2, 3, 11 };

    Solution solution;
    std::vector<int> result = solution.sortedSquares(A); // 调用快速排序算法

    // 打印排序后的数组
    for (auto i = result.begin(); i < result.end(); ++i) {
        std::cout << *i << ' ';
    }
    
    return 0;
}

3.2 双指针法

• 数组其实是有序的，只不过负数平方之后可能成为最大数了。那么数组平方的最大值就在数组的两端，不是最左边就是最右边，不可能是中间。此时可以考虑双指针法了，i 指向起始位置，j 指向终止位置。定义一个新数组 result，和 A 数组一样的大小

  如果 A[i] * A[i] < A[j] * A[j] 那么 result[k--] = A[j] * A[j]; 
  如果 A[i] * A[i] >= A[j] * A[j] 那么 result[k--] = A[i] * A[i];
  

// 时间复杂度：O(n)
#include 
#include 

class Solution {
public:
    std::vector<int> sortedSquares(std::vector<int> &A) {
        std::vector<int> result(A.size());
        // 定义左右指针，初始时分别指向数组的第一个和最后一个元素
        int left = 0;
        int right = A.size() - 1;
        // 从右向左遍历数组
        for (int i = A.size() - 1; i >= 0; --i) {
            // 取左右指针指向的数的平方的较大值添加到结果中，并将左右指针向中间移动
            if (A[left] * A[left] >= A[right] * A[right]) {
                result[i] =  A[left] * A[left];
                ++left;
            } else {
                result[i] = A[right] * A[right];
                --right;
            }
        }
        return result;
    }
};

int main(int argc, char *argv[]) {
    std::vector<int> A{ -7, -3, 2, 3, 11 };
    Solution solution;
    std::vector<int> result = solution.sortedSquares(A); // 调用快速排序算法

    // 打印排序后的数组
    for (auto i = result.begin(); i < result.end(); ++i) {
        std::cout << *i << ' ';
    }
    
    return 0;
}

4. 长度最小的子数组

209. 长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的连续子数组，并返回其长度。如果不存在符合条件的子数组，返回 0

• 示例 1
  输入：s = 7, nums = [2,3,1,2,4,3] 输出：2 解释：子数组 [4,3] 是该条件下的长度最小的子数组
• 提示
  1 <= target <= 10^9
  1 <= nums.length <= 10^5
  1 <= nums[i] <= 10^5

滑动窗口法

• 所谓滑动窗口（也可以理解为双指针法的一种），就是不断的调节子序列的起始位置和终止位置，从而得出要想的结果。在暴力解法中，是一个 for 循环为滑动窗口的起始位置，另一个 for 循环为滑动窗口的终止位置，用两个 for 循环 完成了一个不断搜索区间的过程。那么滑动窗口如何用一个 for 循环来完成这个操作呢？

  • 首先要思考：如果用一个 for 循环，那么应该表示滑动窗口的起始位置，还是终止位置。只用一个 for 循环，那么这个循环的索引，一定是表示滑动窗口的终止位置。那么问题来了，滑动窗口的起始位置如何移动呢？这里还是以题目中的示例来举例，s=7，数组是 2，3，1，2，4，3，来看一下查找的过程

• 在本题中实现滑动窗口，主要确定如下三点

  • 窗口内是什么？
    • 窗口就是满足其和 ≥ s 的长度最小的连续子数组
  • 如何移动窗口的起始位置？
    • 如果当前窗口的值大于 s 了，窗口就要向前移动了（也就是该缩小了）
  • 如何移动窗口的结束位置？
    • 窗口的结束位置就是遍历数组的指针，也就是 for 循环里的索引

• 解题的关键在于窗口的起始位置如何移动，滑动窗口的精妙之处在于，根据当前子序列和大小的情况，不断调节子序列的起始位置，从而将 $O(n^2)$ 暴力解法降为 $O(n)$：每个元素在滑动窗后进来操作一次，出去操作一次，每个元素都是被操作两次，所以时间复杂度是 2n 也就是 $O(n)$
  

// 时间复杂度：O(n)
// 空间复杂度：O(1)
#include 
#include 

class Solution {
public:
    int minSubArrayLen(int target, std::vector<int> &nums) {
        int result = INT32_MAX; // 子数组初始值
        int sum = 0; // 滑动窗口数值之和
        int i = 0; // 滑动窗口起始位置
        int subLength = 0; // 滑动窗口的长度

        for (int j = 0; j < nums.size(); ++j) { // j 滑动窗口终止位置
            sum += nums[j];
            // 使用 while，每次更新 i（起始位置），并不断比较子序列是否符合条件
            while (sum >= target) {
                subLength = (j - i + 1); // 取子序列的长度
                result = result < subLength ? result : subLength;
                sum -= nums[i]; // 不断变更 i（子序列的起始位置）
                ++i;
            }
        }
        // 如果 result 没有被赋值的话，就返回 0，说明没有符合条件的子序列
        return result == INT32_MAX ? 0 : result;
    }
};

int main(int argc, char *argv[]) {
    std::vector<int> nums{ 2, 3, 1, 2, 4, 3 };
    int target = 7;

    Solution solution;
    std::cout << solution.minSubArrayLen(target, nums) << std::endl;
    
    return 0;
}

5. 螺旋矩阵II

59. 螺旋矩阵 II
给定一个正整数 n，生成一个包含 1 到 $n^2$ 所有元素，且元素按顺时针顺序螺旋排列的正方形矩阵

• 示例
  输入: 3 输出: [ [ 1, 2, 3 ], [ 8, 9, 4 ], [ 7, 6, 5 ] ]

5.1 思路

• 核心思想：循环不变量原则
  • 模拟顺时针画矩阵的过程，一圈下来要画每四条边，每画一条边都坚持一致的左闭右开（或左开右闭）原则
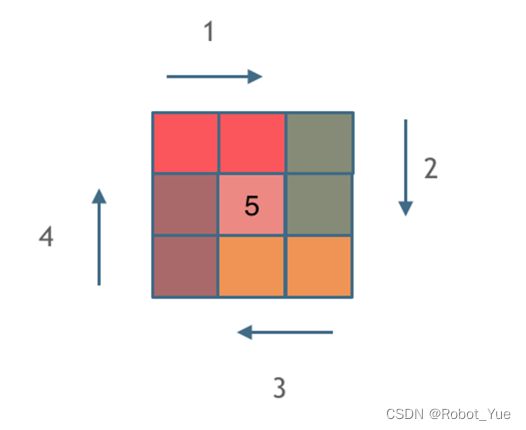
  • 下图每一种颜色代表一条边及遍历的长度，可以看出每一个拐角处的处理规则，拐角处让给新的一条边来继续画，即左闭右开的原则
    • 填充上行从左到右
    • 填充右列从上到下
    • 填充下行从右到左
    • 填充左列从下到上

5.2 代码实现

// 时间复杂度 O(n^2): 模拟遍历二维矩阵的时间
// 空间复杂度 O(1)
#include 
#include 

class Solution {
public:
    std::vector<std::vector<int>> generateMatrix(int n) {
        std::vector<std::vector<int>> res(n, std::vector<int>(n, 0)); // 使用vector定义一个二维数组，每个位置初始化为0
        int startx = 0, starty = 0; // 定义每循环一个圈的起始位置
        int loop = n / 2; // 每个圈循环几次，例如n为奇数3，那么loop = 1 只是循环一圈，矩阵中间的值需要单独处理
        int mid = n / 2; // 矩阵中间的位置，例如：n为3，中间的位置就是(1，1)，n为5，中间位置为(2, 2)
        int count = 1; // 用来给矩阵中每一个空格赋值
        int offset = 1; // 需要控制每一条边遍历的长度，每次循环右边界收缩一位
        int i,j;
        while (loop--) {
            i = startx;
            j = starty;

            // 下面开始的四个for就是模拟转了一圈
            // 模拟填充上行从左到右(左闭右开)
            for (j = starty; j < n - offset; j++) {
                res[i][j] = count++;
            }
            // 模拟填充右列从上到下(左闭右开)
            for (i = startx; i < n - offset; i++) {
                res[i][j] = count++;
            }
            // 模拟填充下行从右到左(左闭右开)
            for (; j > starty; j--) {
                res[i][j] = count++;
            }
            // 模拟填充左列从下到上(左闭右开)
            for (; i > startx; i--) {
                res[i][j] = count++;
            }

            // 第二圈开始的时候，起始位置要各自加1， 例如：第一圈起始位置是(0, 0)，第二圈起始位置是(1, 1)
            startx++;
            starty++;

            // offset 控制每一圈里每一条边遍历的长度
            offset += 1;
        }

        // 如果n为奇数的话，需要单独给矩阵最中间的位置赋值
        if (n % 2) {
            res[mid][mid] = count;
        }
        return res;
    }
};

int main(int argc, char *argv[]) {
    Solution solution;
    int n = 3;

    std::vector<std::vector<int>> res = solution.generateMatrix(n);
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < n; ++j) {
            std::cout << res[i][j] << " ";
        }
        std::cout << std::endl;
    }

    return 0;
}