Java语言----二叉树

目录

一、二叉树

1.1 二叉树概念

1.2 两种特殊的二叉树

1.3二叉树的性质

二 、二叉树的实现

2.1第一种 使用数组

2.2第二种 使用链表实现

 2.2.1二叉树代码构建

 2.2.2二叉树的基本操作

三、二叉树的三种遍历

3.1递归方法实现 前、中、后遍历

3.2非递归方法实现 前、中、后遍历

总结

---

个人主页： 博客-专业IT技术发表平台 (csdn.net)
 梦的目标：努力学习，向Java进发，拼搏一切，让自己的未来不会有遗憾。
 欢迎各位→点赞 + 收藏⭐ + 评论+关注✨
  本章讲解内容：二叉树

来源于百度

  使用编译器：IDEA

一、二叉树

1.1 二叉树概念

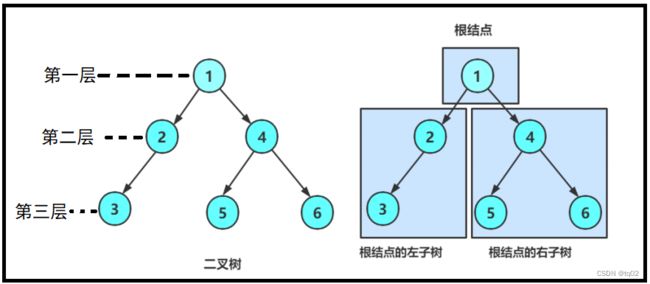
二叉树：一种 非线性 的数据结构，为结点的一个有限集合。

              有限集合分类：1、或者为空     

                                        2、由一个根节点加上两棵别称为 左子树 和 右子树 的二叉树组成

重要知识：

1、树的深度或高度：树的最大层次。如上图：该二叉树高度为3。

2、结点的度：1个结点含有的子树个数。如上图：结点1的度为2，分别为2和4的左右子树。

3、父亲结点：拥有子树的结点。如上图：1便有2和4的子树，所以为父亲结点。

4、孩子结点：一个结点的的子树结点便为孩子结点。如上图：2是1的孩子结点。

5、叶子结点：无子树的结点。如上图：3、5、6的结点无子树，为叶子结点。

6、根结点：最开始的结点。如上图：1为根结点，每个二叉树只有一个根结点。

1.2 两种特殊的二叉树

1. 满二叉树 : 一棵二叉树，如果 每层的结点数都达到最大值，则这棵二叉树就是满二叉树 。也就是说， 如果一棵 二叉树的层数为K，且结点总数是  2^k-1 ，则它就是满二叉树。

2. 完全二叉树 : 一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，从0开始编号，编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同。

红色数字，代表的是结点序号，数组实现时使用 

完全二叉树更为重要，因为堆便是在此基础上实现的。

---

1.3二叉树的性质

1. 若规定 根结点的层数为 1 ，则一棵 非空二叉树的第 i 层上最多有 (i>0) 个结点

2. 若规定只有 根结点的二叉树的深度为 1 ，则 深度为 K 的二叉树的最大结点数是 (k>=0)

3. 对任何一棵二叉树 , 如果其 叶结点个数为 n0, 度为 2 的非叶结点个数为 n2, 则有 n0 ＝ n2 ＋ 1

4. 具有 n 个结点的完全二叉树的深度k为 log2(n+1)  上取整

5. 对于具有 n 个结点的完全二叉树 ，如果按照 从上至下从左至右的顺序对所有节点从 0 开始编号， 则对于 序号为 i 的结点有 ：

        若i>0 ， 双亲序号： (i-1)/2 ； i=0 ， i 为根结点编号 ，无双亲结点

        若2i+1 ，左孩子序号： 2i+1 ，否则无左孩子

        若2i+2 ，右孩子序号： 2i+2 ，否则无右孩子

---

二 、二叉树的实现

实现方法为2种。

        第一种： 使用数组，顺序存储二叉树结点。

        第二种： 使用链表的链式存储。

         此处我们使用链表实现

2.1第一种 使用数组

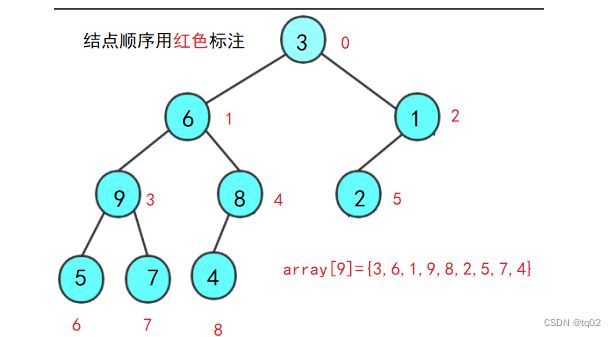
 红色标注的是结点的下标值，一层一层放入array数组里。

 特点：父结点=（孩子结点-1) / 2   此时的结点 等于 数组的下标值。

2.2第二种 使用链表实现

 二叉树的链式存储：通过一个一个的节点引用起来的，因此可以通过链表的方式实现。

 2.2.1二叉树代码构建

public class BinaryTree{
    // 孩子表示法
    class Node {
      int val; // 数据域，代表结点的值
      Node left; // 左孩子的引用，常常代表左孩子为根的整棵左子树
      Node right; // 右孩子的引用，常常代表右孩子为根的整棵右子树
      Node(){}
      Node(int num)
     {
        this.val=num;
     }
  }

private Node root;

//构建二叉树
public void createBinaryTree(){
Node node1 = new Node(1);
Node node1 = new Node(2);
Node node1 = new Node(3);
Node node1 = new Node(4);
Node node1 = new Node(5);
Node node1 = new Node(6);
root = node1;
node1.left = node2;
node2.left = node3;
node1.right = node4;
node4.left = node5;
node5.right = node6;
}
// 获取树中节点的个数
public int size(Node root);
// 获取叶子节点的个数
public int getLeafNodeCount(Node root);
// 获取第K层节点的个数
public int getKLevelNodeCount(Node root,int k);
// 获取二叉树的高度
public int getHeight(Node root);
// 检测值为value的元素是否存在
public Node find(Node root, int val);
//层序遍历
public void levelOrder(Node root);
// 判断一棵树是不是完全二叉树
public boolean isCompleteTree(Node root);

}

2.2.2二叉树的基本操作

获取二叉树结点个数：

public int size(Node root)
{
   if(root==null)
  return 0;
  return size(root.left)+size(root.right)+1;
}

获取叶子结点个数：

// 获取叶子节点的个数
    public int getLeafNodeCount(Node root)
    {
        if(root==null)
        {
            return 0;
        }
        if(root.left==null&&root.right==null)
            return 1;
        return getLeafNodeCount(root.left)+getLeafNodeCount(root.right);
    }

 获取第k层结点个数：

public int getKLevelNodeCount(TreeNode root, int k) {
        if(root == null) {
            return 0;
        }
        if(k == 1) {
            return 1;
        }
        return getKLevelNodeCount(root.left,k-1)
                + getKLevelNodeCount(root.right,k-1);
    }

 获取二叉树高度：

public  int getHeight(TreeNode root) {
        if(root == null) {
            return 0;
        }
        int leftH = getHeight(root.left);
        int rightH = getHeight(root.right);

        return (leftH > rightH ? leftH :rightH) + 1;
    }

检测是否存在value值：

 public TreeNode find(TreeNode root,int val) {
        if(root == null) return null;
        if(root.val == val) {
            return root;
        }
        TreeNode leftL = find(root.left,val);
        if(leftL != null) {
            return leftL;
        }
        TreeNode leftLR = find(root.right,val);
        if(leftLR != null) {
            return leftLR;
        }
        return null;
    }

层序遍历：

 public void levelOrder(TreeNode root) {
        Queue queue = new LinkedList<>();
       if(root != null) {
           queue.offer(root);
       }
       while (!queue.isEmpty()) {
           TreeNode top = queue.poll();
           System.out.print(top.val+" ");
           if(top.left != null) {
               queue.offer(top.left);
           }
           if(top.right != null) {
               queue.offer(top.right);
           }
       }

    }

 是否为完全二叉树：

 public boolean isCompleteTree(TreeNode root) {
        Queue queue = new LinkedList<>();
        if(root != null) {
            queue.offer(root);
        }
        while (!queue.isEmpty()) {
            Node cur = queue.poll();
            if(cur != null) {
                queue.offer(cur.left);
                queue.offer(cur.right);
            }else {
                break;
            }
        }
        while (!queue.isEmpty()) {
           Node cur = queue.poll();
            if(cur != null) {
                return false;
            }
        }
        return true;
    }

三、二叉树的三种遍历

二叉树有四种遍历方法：前序遍历、中序遍历、后序遍历已经层序遍历。

前序遍历：访问根结点--->根的左子树--->根的右子树         （根-左-右）

中序遍历：根的左子树--->根节点--->根的右子树                （左-根-右）

后序遍历：根的左子树--->根的右子树--->根节点                （左-右-根）

3.1递归方法实现 前、中、后遍历

前序遍历：

 public void preOrder(TreeNode root) {
        if(root == null) return;
        System.out.print(root.val+" ");
        preOrder(root.left);
        preOrder(root.right);
    }

中序遍历：

 public void inOrder(TreeNode root) {
        if(root == null) return;
        inOrder(root.left);
        System.out.print(root.val+" ");
        inOrder(root.right);
    }

后序遍历：

 public void postOrder(TreeNode root) {
        if(root == null) return;
        postOrder(root.left);
        postOrder(root.right);
        System.out.print(root.val+" ");
    }

3.2非递归方法实现 前、中、后遍历

前序遍历：

public void preOrderIteration(TreeNode head) {
    if(head==null){
       return;
    }
Stack stack=new Stack<>();
stack.push(head);
    while(！stack.isEmpty())
    {
        TreeNOde node=stack.pop();
        System.out.print(node.val+" ");
        if(node.right!=null)
        {
            stack.push(node.left);
        }
        if(node.left!=null){
            stack.push(node.right);
        }
    }
}

利用栈的原理

中序遍历：

 public void inOrderIteration(TreeNode head) {
    if(head==null){
       return;
    }
    Stack stack=new Stack<>();
    TreeNode cur=head;
    while(!stack.isEmpty())
    {
        while(cur!=null)
        {
          stack.push(cur);
          cur=cur.left;
        }
        TreeNode node=stack.pop();
        System.out.print(node.val+"");
        if(node.right!=null)
        {
            cur=node.right;
        }
    }
}

后序遍历：

public static void postOrderIteration(TreeNode head) {
        if (head == null) {
            return;
        }
        Stack stack1 = new Stack<>();
        Stack stack2 = new Stack<>();
        stack1.push(head);
        while (!stack1.isEmpty()) {
            TreeNode node = stack1.pop();
            stack2.push(node);
            if (node.left != null) {
                stack1.push(node.left);
            }
            if (node.right != null) {
                stack1.push(node.right);
            }
        }
        while (!stack2.isEmpty()) {
            System.out.print(stack2.pop().val + " ");
        }
    }

总结

         无论是链表实现，还是数组实现，各有其优势，不同情况使用，而不是代表链表实现比数组更好。二叉树里最重要的是完全二叉树，而在它基础上又实现了另一个数据结构，堆。在Java中更含有对应的实现类 PriorityQueue 。